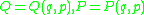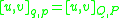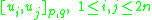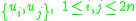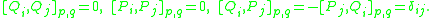Lagrange bracket
Encyclopedia
Lagrange brackets are certain expressions closely related to Poisson bracket
s that were introduced by Joseph Louis Lagrange
in 1808–1810 for the purposes of mathematical formulation of classical mechanics
, but unlike the Poisson brackets, have fallen out of use.
on a phase space
. If each of them is expressed as a function of two variables, u and v, then the Lagrange bracket of u and v is defined by the formula

Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s that were introduced by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1808–1810 for the purposes of mathematical formulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, but unlike the Poisson brackets, have fallen out of use.
Definition
Suppose that (q1, …, qn, p1, …, pn) is a system of canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
on a phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. If each of them is expressed as a function of two variables, u and v, then the Lagrange bracket of u and v is defined by the formula

Properties
- Lagrange brackets do not depend on the system of canonical coordinatesCanonical coordinatesIn mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
(q, p). If (Q,P) = (Q1, …, Qn, P1, …, Pn) is another system of canonical coordinates, so that
- is a canonical transformationCanonical transformationIn Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
, then the Lagrange bracket is an invariant of the transformation, in the sense that
- Therefore, the subscripts indicating the canonical coordinates are often omitted.
- If Ω is the symplectic form on the 2n-dimensional phase space W and u1,…,u2n form a system of coordinates on W, then canonical coordinates (q,p) may be expressed as functions of the coordinates u and the matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of the Lagrange brackets
- represents the components of Ω, viewed as a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, in the coordinates u. This matrix is the inverse of the matrix formed by the Poisson brackets
- of the coordinates u.
- As a corollary of the preceding properties, coordinates (Q1, …, Qn, P1, …, Pn) on a phase space are canonical if and only if the Lagrange brackets between them have the form