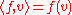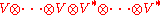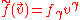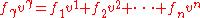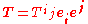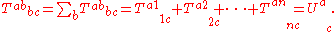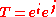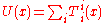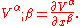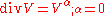Tensor contraction
Encyclopedia
In multilinear algebra
, a tensor contraction is an operation on one or more tensor
s that arises from the natural pairing of a finite-dimension
al vector space
and its dual. In components, it is expressed as a sum of products of scalar components of the tensor(s) caused by applying the summation convention to a pair of dummy indices which are bound to each other in an expression. The contraction of a single mixed tensor
occurs when a pair of literal indices (one a subscript, the other a superscript) of the tensor are set equal to each other and summed over. In the Einstein notation
this summation is built into the notation. The result is another tensor
with rank (or order) reduced by 2.
Tensor contraction can be seen as a generalization of the trace
.
k. The core of the contraction operation, and the simplest case, is the natural
pairing of V with its dual vector space V*. The pairing is the linear transformation
from the tensor product of these two spaces to the field k:
corresponding to the bilinear form
where f is in V* and v is in V. The map C defines the contraction operation on a tensor of type (1,1), which is an element of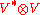 . Note that the result is a scalar
. Note that the result is a scalar
(an element of k). Using the natural isomorphism between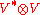 and the space of linear transformations from V to V, one obtains a basis-free definition of the trace
and the space of linear transformations from V to V, one obtains a basis-free definition of the trace
.
In general, a tensor
of type (m, n) (with m ≥ 1 and n ≥ 1) is an element of the vector space
(where there are m V factors and n V* factors). Applying the natural pairing to the kth V factor and the lth V* factor, and using the identity on all other factors, defines the (k, l) contraction operation, which is a linear map which yields a tensor of type (m − 1, n − 1). By analogy with the (1,1) case, the general contraction operation is sometimes called the trace.
, the basic contraction of a vector and a dual vector is denoted by
which is shorthand for the explicit coordinate summation
(where vi are the components of v in a particular basis and fi are the components of f in the corresponding dual basis).
Since a general mixed dyadic tensor
is a linear combination of decomposable tensors of the form , the explicit formula for the dyadic case follows: let
, the explicit formula for the dyadic case follows: let
be a mixed dyadic tensor. Then its contraction is
A general contraction is denoted by labeling one covariant index and one contravariant index with the same letter, summation over that index being implied by the summation convention. The resulting contracted tensor inherits the remaining indices of the original tensor. For example, contracting a tensor T of type (2,2) on the second and third indices to create a new tensor U of type (1,1) is written as
By contrast, let
be an unmixed dyadic tensor. This tensor does not contract; if its base vectors are dotted the result is the contravariant metric tensor
,
whose rank is 2.
) g, such contractions are possible. One uses the metric to raise or lower one of the indices, as needed, and then one uses the usual operation of contraction. The combined operation is known as metric contraction.
, manifold
s, or schemes
). Since contraction is a purely algebraic operation, it can be applied pointwise to a tensor field, e.g. if T is a (1,1) tensor field on Euclidean space, then in any coordinates, its contraction (a scalar field) U at a point x is given by
Since the role of x is not complicated here, it is often suppressed, and the notation for tensor fields becomes identical to that for purely algebraic tensors.
Over a Riemannian manifold
, a metric (field of inner products) is available, and both metric and non-metric contractions are crucial to the theory. For example, the Ricci tensor is a non-metric contraction of the Riemann curvature tensor
, and the scalar curvature
is the unique metric contraction of the Ricci tensor.
One can also view contraction of a tensor field in the context of modules over an appropriate ring of functions on the manifold or the context of sheaves of modules over the structure sheaf; see the discussion at the end of this article.
on a Riemannian manifold
(for example, Euclidean space
). Let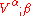 be the covariant derivative
be the covariant derivative
of V (in some choice of coordinates). In the case of Cartesian coordinates in Euclidean space, one can write
Then changing index β to α causes the pair of indices to become bound to each other, so that the derivative contracts with itself to obtain the following sum:
which is the divergence
div V. Then
is a continuity equation
for V.
In general, one can define various divergence operations on higher-rank tensor fields, as follows. If T is a tensor field with at least one contravariant index, taking the covariant differential and contracting the chosen contravariant index with the new covariant index corresponding to the differential results in a new tensor of rank one lower than that of T.
 is a new tensor, which, if it has at least one covariant and one contravariant index, can be contracted. The case where T is a vector and U is a dual vector is exactly the core operation introduced first in this article.
is a new tensor, which, if it has at least one covariant and one contravariant index, can be contracted. The case where T is a vector and U is a dual vector is exactly the core operation introduced first in this article.
In abstract index notation, to contract two tensors with each other, one places them side by side (juxtaposed) as factors of the same term. This implements the tensor product, yielding a composite tensor. Contracting two indices in this composite tensor implements the desired contraction of the two tensors.
For example, matrices can be represented as tensors of type (1,1) with the first index being contravariant and the second index being covariant. Let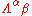 be the components of one matrix and let
be the components of one matrix and let 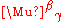 be the components of a second matrix. Then their multiplication is given by the following contraction, an example of the contraction of a pair of tensors:
be the components of a second matrix. Then their multiplication is given by the following contraction, an example of the contraction of a pair of tensors:
Also, the interior product of a vector with a differential form
is a special case of the contraction of two tensors with each other.
and let M be a finite free module
over R. Then contraction operates on the full (mixed) tensor algebra of M in exactly the same way as it does in the case of vector spaces over a field. (The key fact is that the natural pairing is still perfect in this case.)
More generally, let OX be a sheaf
of commutative rings over a topological space
X, e.g. OX could be the structure sheaf of a complex manifold
, analytic space
, or scheme
. Let M be a locally free sheaf of modules over OX of finite rank. Then the dual of M is still well-behaved and contraction operations make sense in this context.
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, a tensor contraction is an operation on one or more tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s that arises from the natural pairing of a finite-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and its dual. In components, it is expressed as a sum of products of scalar components of the tensor(s) caused by applying the summation convention to a pair of dummy indices which are bound to each other in an expression. The contraction of a single mixed tensor
Mixed tensor
In tensor analysis, a mixed tensor is a tensor which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript and at least one of the indices will be a superscript ....
occurs when a pair of literal indices (one a subscript, the other a superscript) of the tensor are set equal to each other and summed over. In the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
this summation is built into the notation. The result is another tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
with rank (or order) reduced by 2.
Tensor contraction can be seen as a generalization of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
Abstract formulation
Let V be a vector space over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k. The core of the contraction operation, and the simplest case, is the natural
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
pairing of V with its dual vector space V*. The pairing is the linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
from the tensor product of these two spaces to the field k:
corresponding to the bilinear form
where f is in V* and v is in V. The map C defines the contraction operation on a tensor of type (1,1), which is an element of
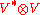 . Note that the result is a scalar
. Note that the result is a scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
(an element of k). Using the natural isomorphism between
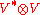 and the space of linear transformations from V to V, one obtains a basis-free definition of the trace
and the space of linear transformations from V to V, one obtains a basis-free definition of the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
In general, a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of type (m, n) (with m ≥ 1 and n ≥ 1) is an element of the vector space
(where there are m V factors and n V* factors). Applying the natural pairing to the kth V factor and the lth V* factor, and using the identity on all other factors, defines the (k, l) contraction operation, which is a linear map which yields a tensor of type (m − 1, n − 1). By analogy with the (1,1) case, the general contraction operation is sometimes called the trace.
Contraction in index notation
In abstract index notationAbstract index notation
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...
, the basic contraction of a vector and a dual vector is denoted by
which is shorthand for the explicit coordinate summation
(where vi are the components of v in a particular basis and fi are the components of f in the corresponding dual basis).
Since a general mixed dyadic tensor
Dyadic tensor
In multilinear algebra, a dyadic is a second rank tensor written in a special notation, formed by juxtaposing pairs of vectors, along with a notation for manipulating such expressions analogous to the rules for matrix algebra....
is a linear combination of decomposable tensors of the form
 , the explicit formula for the dyadic case follows: let
, the explicit formula for the dyadic case follows: letbe a mixed dyadic tensor. Then its contraction is
-
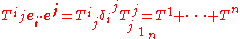 .
.
A general contraction is denoted by labeling one covariant index and one contravariant index with the same letter, summation over that index being implied by the summation convention. The resulting contracted tensor inherits the remaining indices of the original tensor. For example, contracting a tensor T of type (2,2) on the second and third indices to create a new tensor U of type (1,1) is written as
By contrast, let
be an unmixed dyadic tensor. This tensor does not contract; if its base vectors are dotted the result is the contravariant metric tensor
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
,
-
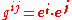 ,
,
whose rank is 2.
Metric contraction
As in the previous example, contraction on a pair of indices that are either both contravariant or both covariant is not possible in general. However, in the presence of an inner product (also known as a metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
) g, such contractions are possible. One uses the metric to raise or lower one of the indices, as needed, and then one uses the usual operation of contraction. The combined operation is known as metric contraction.
Application to tensor fields
Contraction is often applied to tensor fields over spaces (e.g. Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, or schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
). Since contraction is a purely algebraic operation, it can be applied pointwise to a tensor field, e.g. if T is a (1,1) tensor field on Euclidean space, then in any coordinates, its contraction (a scalar field) U at a point x is given by
Since the role of x is not complicated here, it is often suppressed, and the notation for tensor fields becomes identical to that for purely algebraic tensors.
Over a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, a metric (field of inner products) is available, and both metric and non-metric contractions are crucial to the theory. For example, the Ricci tensor is a non-metric contraction of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, and the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
is the unique metric contraction of the Ricci tensor.
One can also view contraction of a tensor field in the context of modules over an appropriate ring of functions on the manifold or the context of sheaves of modules over the structure sheaf; see the discussion at the end of this article.
Tensor divergence
As an application of the contraction of a tensor field, let V be a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(for example, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
). Let
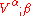 be the covariant derivative
be the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of V (in some choice of coordinates). In the case of Cartesian coordinates in Euclidean space, one can write
Then changing index β to α causes the pair of indices to become bound to each other, so that the derivative contracts with itself to obtain the following sum:
which is the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
div V. Then
is a continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
for V.
In general, one can define various divergence operations on higher-rank tensor fields, as follows. If T is a tensor field with at least one contravariant index, taking the covariant differential and contracting the chosen contravariant index with the new covariant index corresponding to the differential results in a new tensor of rank one lower than that of T.
Contraction of a pair of tensors
One can generalize the core contraction operation (vector with dual vector) in a slightly different way, by considering a pair of tensors T and U. The tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
 is a new tensor, which, if it has at least one covariant and one contravariant index, can be contracted. The case where T is a vector and U is a dual vector is exactly the core operation introduced first in this article.
is a new tensor, which, if it has at least one covariant and one contravariant index, can be contracted. The case where T is a vector and U is a dual vector is exactly the core operation introduced first in this article.In abstract index notation, to contract two tensors with each other, one places them side by side (juxtaposed) as factors of the same term. This implements the tensor product, yielding a composite tensor. Contracting two indices in this composite tensor implements the desired contraction of the two tensors.
For example, matrices can be represented as tensors of type (1,1) with the first index being contravariant and the second index being covariant. Let
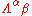 be the components of one matrix and let
be the components of one matrix and let 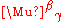 be the components of a second matrix. Then their multiplication is given by the following contraction, an example of the contraction of a pair of tensors:
be the components of a second matrix. Then their multiplication is given by the following contraction, an example of the contraction of a pair of tensors:-
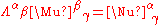 .
.
Also, the interior product of a vector with a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
is a special case of the contraction of two tensors with each other.
More general algebraic contexts
Let R be a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and let M be a finite free module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over R. Then contraction operates on the full (mixed) tensor algebra of M in exactly the same way as it does in the case of vector spaces over a field. (The key fact is that the natural pairing is still perfect in this case.)
More generally, let OX be a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of commutative rings over a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, e.g. OX could be the structure sheaf of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
, analytic space
Analytic space
An analytic space in the theory of functions of several complex variables is a generalization of the concept of an analytic manifold: heuristically, an analytic space is a set which is locally isomorphic to an analytic variety, while an analytic manifold is locally isomorphic to a complex euclidean...
, or scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. Let M be a locally free sheaf of modules over OX of finite rank. Then the dual of M is still well-behaved and contraction operations make sense in this context.
See also
- Tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
- Partial tracePartial traceIn linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
- Interior product
- Raising and lowering indicesRaising and lowering indicesIn mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
- Musical isomorphismMusical isomorphismIn mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....