Dirac large numbers hypothesis - AbsoluteAstronomy.com

The Dirac large numbers hypothesis (LNH) is an observation made by Paul Dirac

Paul Dirac

Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...

in 1937 relating ratios of size scales in the Universe

Universe

The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...

to that of force scales. The ratios constitute very large, dimensionless numbers: some 40 orders of magnitude in the present cosmological epoch. According to Dirac's hypothesis, the apparent equivalence of these ratios might not be a mere coincidence but instead could imply a cosmology

Physical cosmology

Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...

with these unusual features:

The strength of gravity, as represented by the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

, is inversely proportional to the age of the universe: ;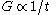
The mass of the universe is proportional to the square of the universe's age: .

Neither of these two features has gained acceptance in mainstream physics and, though some proponents of non-standard cosmologies

Non-standard cosmology

A non-standard cosmology is any physical cosmological model of the universe that has been, or still is, proposed as an alternative to the big bang model of standard physical cosmology...

refer to Dirac's cosmology as a foundational basis for their own ideas and studies, some physicists harshly dismiss the large numbers in LNH as mere coincidences more suited to numerology

Numerology

Numerology is any study of the purported mystical relationship between a count or measurement and life. It has many systems and traditions and beliefs...

than physics. A coincidence, however, may be defined optimally as 'an event that provides support for an alternative to a currently favoured causal theory, but not necessarily enough support to accept that alternative in light of its low prior probability.' Research into LNH, or the large number of coincidences that underpin it, appears to have gained new impetus from failures in standard cosmology to account for anomalies such as the recent discovery that the universe might be expanding at an accelerated rate.

Background

LNH was Dirac's personal response to a set of large number 'coincidences' that had intrigued other theorists at about the same time. The 'coincidences' began with Hermann Weyl

Hermann Weyl

Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...

(1919), who speculated that the observed radius of the universe might also be the hypothetical radius of a particle whose energy is equal to the gravitational self-energy of the electron:

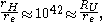
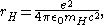
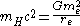
where r_e is the classical electron radius

Classical electron radius

The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...

, m_e is the mass of the electron, m_H denotes the mass of the hypothetical particle, r_H is its electrostatic radius and R_U is the radius of the observable universe.

The coincidence was further developed by Arthur Eddington (1931) who related the above ratios to N, the estimated number of charged particles in the Universe:

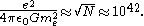
In addition to the examples of Weyl and Eddington, Dirac was influenced also by the primeval-atom hypothesis of Georges Lemaitre

Georges Lemaître

Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...

, who lectured on the topic in Cambridge in 1933. The notion of a varying-G cosmology first appears in the work of Edward Arthur Milne a few years before Dirac formulated LNH. Milne was inspired not by large number coincidences but by a dislike of Einstein's general theory of relativity. For Milne, space was not a structured object but simply a system of reference in which Einstein's conclusions could be accommodated by relations such as this:

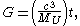
where M_U is the mass of the universe and t is the age of the universe in seconds. According to this relation, G increases over time.

Dirac's interpretation of the large number coincidences

The Weyl and Eddington ratios above can be rephrased in a variety of ways, as for instance in the context of time: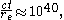

where t is the age of the universe,

is the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

and r_e is the classical electron radius. Hence, in atomic units where c=1 and r_e = 1, the age of the Universe is about 10⁴⁰ atomic units of time. This is the same order of magnitude

Order of magnitude

An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...

as the ratio of the electrical to the gravitational force

Force

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...

s between a proton

Proton

The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....

and an electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

Hence, interpreting the charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

of the electron

Electron

, the mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

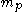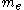of the proton/electron, and the permittivity factor

in atomic units (equal to 1), the value of the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

is approximately 10⁻⁴⁰. Dirac interpreted this to mean that

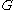varies with time as

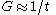, and thereby pointed to a cosmology

Physical cosmology

that seems 'designer-made' for a theory of quantum gravity

Quantum gravity

Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...

. According to general relativity, however, G is constant, otherwise the law of conserved energy is violated. Dirac met this difficulty by introducing into the Einstein equations a gauge function that describes the structure of spacetime in terms of a ratio of gravitational and electromagnetic units. He also provided alternative scenarios for the continuous creation of matter, one of the other significant issues in LNH:

'additive' creation (new matter is created uniformly throughout space) and
'multiplicative' creation (new matter is created where there are already concentrations of mass).

Later developments and interpretations

Dirac's theory has inspired and continues to inspire a significant body of scientific literature in a variety of disciplines. In the context of geophysics, for instance, Edward Teller

Edward Teller

Edward Teller was a Hungarian-American theoretical physicist, known colloquially as "the father of the hydrogen bomb," even though he did not care for the title. Teller made numerous contributions to nuclear and molecular physics, spectroscopy , and surface physics...

seemed to raise a serious objection to LNH in 1948 when he argued that variations in the strength of gravity are not consistent with paleontological data. However, George Gamow

George Gamow

George Gamow , born Georgiy Antonovich Gamov , was a Russian-born theoretical physicist and cosmologist. He discovered alpha decay via quantum tunneling and worked on radioactive decay of the atomic nucleus, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, cosmic microwave...

demonstrated in 1962 how a simple revision of the parameters (in this case, the age of the solar system) can invalidate Teller's conclusions. The debate is further complicated by the choice of LNH cosmologies

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

: In 1978, G. Blake argued that paleontological data is consistent with the 'multiplicative' scenario but not the 'additive' scenario. Arguments both for and against LNH are also made from astrophysical considerations. For example, D. Falik argued that LNH is inconsistent with experimental results for microwave background radiation whereas Canuto and Hsieh argued that it is consistent. One argument that has created significant controversy was put forward by Robert Dicke in 1961. Known as the anthropic coincidence or fine-tuned universe

Fine-tuned universe

The fine-tuned universe is the proposition that the conditions that allow life in the Universe can only occur when certain universal fundamental physical constants lie within a very narrow range, so that if any of several fundamental constants were only slightly different the universe would be...

, it simply states that the large numbers in LNH are a necessary coincidence for intelligent beings since they parametrize fusion

Nuclear fusion

Nuclear fusion is the process by which two or more atomic nuclei join together, or "fuse", to form a single heavier nucleus. This is usually accompanied by the release or absorption of large quantities of energy...

of hydrogen

Hydrogen

Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...

in star

Star

A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

s and hence carbon-based life

Life

Life is a characteristic that distinguishes objects that have signaling and self-sustaining processes from those that do not, either because such functions have ceased , or else because they lack such functions and are classified as inanimate...

would not arise otherwise.

Various authors have introduced new sets of numbers into the original 'coincidence' considered by Dirac and his contemporaries, thus broadening or even departing from Dirac's own conclusions. Jordan (1947) noted that the mass ratio for a typical star and an electron approximates to 10⁶⁰, an interesting variation on the 10⁴⁰ and 10⁸⁰ that are typically associated with Dirac and Eddington respectively. Various numbers of the order of 10⁶⁰ were arrived at by V. E. Shemi-Zadah (2002) through measuring cosmological entities in Planck units

Planck units

In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...

. P. Zizzi (1998) argued that there might be a modern mathematical interpretation of LNH in a Planck-scale setting in the context of quantum foam

Quantum foam

Quantum foam, also referred to as spacetime foam, is a concept in quantum mechanics, devised by John Wheeler in 1955. The foam is supposed to be the foundations of the fabric of the universe. Additionally, it can be used as a qualitative description of subatomic spacetime turbulence at extremely...

. The relevance of the Planck scale to LNH was further demonstrated by S. Caneiro and G. Marugan (2002) by reference to the holographic principle

Holographic principle

The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...

. Previously, Carneiro (1997) arrived at an intermediate scaling factor 10²⁰ when considering the possible quantization of cosmic structures and a rescaling of Planck's constant.

Several authors have recently identified and pondered the significance of yet another large number, approximately 120 orders of magnitude. This is for example the ratio of the theoretical and observational estimates of the energy density of the vacuum

Vacuum

In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...

, which Nottale (1993) and Matthews (1997) associated in an LNH context with a scaling law for the cosmological constant

Cosmological constant

In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...

. Carl Friedrich von Weizsaecker identified 10¹²⁰ with the ratio of the universe's volume to the volume of a typical nucleon bounded by its Compton wavelength, and he identified this ratio with the sum of elementary events or bit

Bit

A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...

s of information

Information

Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...

in the universe. T. Goernitz (1986), building on Weizsaecker's work, posited an explanation for large number 'coincidences' in the context of Bekenstein–Hawking entropy

Entropy

Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

. Genreith (1999) has sketched out a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

cosmology in which the smallest mass, which he identified as a neutrino

Neutrino

A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...

, is about 120 orders of magnitude smaller than the mass of the universe (note: this 'neutrino' approximates in scale to the hypothetical particle m_H mentioned above in the context of Weyl's work in 1919). Sidharth (2005) interpreted a typical electromagnetic particle such as the pion

Pion

In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....

as a collection of 10⁴⁰ Planck oscillators and the universe as a collection of 10¹²⁰ Planck oscillators. The fact that a number like 10¹²⁰ can be represented in a variety of ways has been interpreted by Funkhouser (2006) as a new large numbers coincidence. Funkhouser claimed to have 'resolved' the LNH coincidences without departing from the standard model

Standard Model

The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...

for cosmology. In a similar vein, Carneiro and Marugan (2002) claimed that the scaling relations in LNH can be explained entirely according to basic principles.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.