
Nondimensionalization
Encyclopedia
Nondimensionalization is the partial or full removal of unit
s from an equation involving physical quantities
by a suitable substitution of variables
. This technique can simplify and parameterize
problems where measured
units are involved. It is closely related to dimensional analysis
. In some physical system
s, the term scaling is used interchangeably with nondimensionalization, in order to suggest that certain quantities are better measured relative to some appropriate unit. These units refer to quantities intrinsic to the system, rather than units such as SI
units. Nondimensionalization is not the same as converting extensive quantities
in an equation to intensive quantities, since the latter procedure results in variables that still carry units.
Nondimensionalization can also recover characteristic properties of a system. For example, if a system has an intrinsic resonance frequency
, length
, or time constant
, nondimensionalization can recover these values. The technique is especially useful for systems that can be described by differential equation
s. One important use is in the analysis of control system
s.
One of the simplest characteristic units is the doubling time
of a system experiencing exponential growth
, or conversely the half-life
of a system experiencing exponential decay; a more natural pair of characteristic units is mean age/mean lifetime, which correspond to base e rather than base 2.
Many illustrative examples of nondimensionalization originate from simplifying differential equations. This is because a large body of physical problems can be formulated in terms of differential equations. Consider the following:
Although nondimensionalization is well adapted for these problems, it is not restricted to them. An example of a non-differential-equation application is dimensional analysis, while another is normalization
in statistics
.
Measuring device
s are practical examples of nondimensionalization occurring in everyday life. Measuring devices are calibrated relative to some known unit. Subsequent measurements are made relative to this standard. Then, the absolute value of the measurement is recovered by scaling with respect to the standard.
is swinging with a particular period
T. For such a system, it is advantageous to perform calculations relating to the swinging relative to T. In some sense, this is normalizing the measurement with respect to the period.
Measurements made relative to an intrinsic property of a system will apply to other systems which also have the same intrinsic property. It also allows one to compare a common property of different implementations of the same system. Nondimensionalization determines in a systematic manner the characteristic units of a system to use, without relying heavily on prior knowledge of the system's intrinsic properties
(one should not confuse characteristic units of a system with natural units
of nature). In fact, nondimensionalization can suggest the parameters which should be used for analyzing a system. However, it is necessary to start with an equation that describes the system appropriately.
The last three steps are usually specific to the problem where nondimensionalization is applied. However, almost all systems require the first two steps to be performed.
As an illustrative example, consider a first order differential equation with constant coefficients
:
of t. Both x and t represent quantities with units. To scale these two variables, assume there are two intrinsic units of measurement xc and tc with the same units as x and t respectively, such that these conditions hold:


These equations are used to replace x and t when nondimensionalizing. If differential operators are needed to describe the original system, their scaled counterparts become dimensionless differential operators.
In this article, the following conventions have been used:
A subscripted c added to a quantity's variable-name is used to denote the characteristic unit used to scale that quantity. For example, if x is a quantity, then xc is the characteristic unit used to scale it.

The dimensionless differential operators with respect to the independent variable becomes
f(t), then

Hence, the new forcing function F is made to be dependent on the dimensionless quantity τ.

The derivation of the characteristic units for this system gives



This new equation is not dimensionless, although all the variables with units are isolated in the coefficients. Dividing by the coefficient of the highest ordered term, the equation becomes

Now it is necessary to determine the quantities of xc and tc so that the coefficients become normalized. Since there are two free parameters, at most only two coefficients can be made to equal unity.
Both substitutions are valid. However, for pedagogical reasons, the latter substitution is used for second order systems. Choosing this substitution allows xc to be determined by normalizing the coefficient of the forcing function:

The differential equation becomes
The coefficient of the first order term is unitless. Define
The factor 2 is present so that the solutions can be parameterized in terms of ζ. In the context of mechanical or electrical systems, ζ is known as the damping ratio
, and is an important parameter required in the analysis of control system
s. 2ζ is also known as the linewidth of the system. The result of the definition is the universal oscillator equation.

The function f(t) is known as the forcing function
.
If the differential equation only contains real (not complex) coefficients, then the properties of such a system behaves as a mixture of first and second order systems only. This is because the roots of its characteristic polynomial
are either real
, or complex conjugate
pairs. Therefore, understanding how nondimensionalization applies to first and second ordered systems allows the properties of higher order systems to be determined through superposition
.
The number of free parameters in a nondimensionalized form of a system increases with its order. For this reason, nondimensionalization is rarely used for higher order differential equations. The need for this procedure has also been reduced with the advent of symbolic computation
.
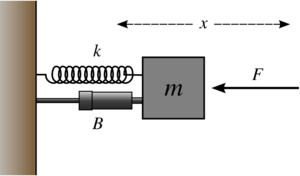 Suppose we have a mass attached to a spring and a damper, which in turn are attached to a wall, and a force acting on the mass along the same line.
Suppose we have a mass attached to a spring and a damper, which in turn are attached to a wall, and a force acting on the mass along the same line.
Define
Suppose the applied force is a sinusoid F = F0 cos(ωt), the differential equation that describes the motion of the block is

Nondimensionalizing this equation the same way as described under second order system yields several characteristics of the system.
The intrinsic unit xc corresponds to the distance the block moves per unit force

The characteristic variable tc is equal to the period of the oscillations

and the dimensionless variable 2ζ corresponds to the linewidth of the system. ζ itself is the damping ratio
.

For a series RC
attached to a voltage source

with substitutions
The first characteristic unit corresponds to the total charge
in the circuit. The second characteristic unit corresponds to the time constant
for the system.
For a series configuration of R,C,L components where Q is the charge in the system
with the substitutions
The first variable corresponds to the maximum charge stored in the circuit. The resonance frequency is given by the reciprocal of the characteristic time. The last expression is the linewidth of the system. The Ω can be considered as a normalized forcing function frequency.
for the one dimensional time independent quantum harmonic oscillator
is

The modulus square of the wavefunction
|ψ|^2 represents probability, which is in a sense already dimensionless and normalized. Therefore, there is no need to nondimensionalize the wavefunction. However, it should be rewritten as a function of a dimensionless variable. Furthermore, the variable x has units of length. Hence substitute
The differential equation becomes
To make the term in front of χ² unitless, set
Hence, the fully nondimensionalized equation is
The nondimensionalization factor for the energy is the same as the ground state
of the harmonic oscillator. Usually, the energy term is not made dimensionless because a primary emphasis of quantum mechanics is determining the energies of the states of a system. Rearranging the first equation, the familiar equation for the harmonic oscillator is

, the analogous process is usually dividing a difference (a distance) by a scale factor (a measure of statistical dispersion
), which yields a dimensionless number, which is called normalization
. Most often, this is dividing errors or residuals
by the standard deviation
or sample standard deviation, respectively, yielding standard score
s and studentized residual
s.
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
s from an equation involving physical quantities
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
by a suitable substitution of variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. This technique can simplify and parameterize
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
problems where measured
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
units are involved. It is closely related to dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
. In some physical system
System
System is a set of interacting or interdependent components forming an integrated whole....
s, the term scaling is used interchangeably with nondimensionalization, in order to suggest that certain quantities are better measured relative to some appropriate unit. These units refer to quantities intrinsic to the system, rather than units such as SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
units. Nondimensionalization is not the same as converting extensive quantities
Intensive and extensive properties
In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...
in an equation to intensive quantities, since the latter procedure results in variables that still carry units.
Nondimensionalization can also recover characteristic properties of a system. For example, if a system has an intrinsic resonance frequency
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
, length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, or time constant
Time constant
In physics and engineering, the time constant, usually denoted by the Greek letter \tau , is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant system.Concretely, a first-order LTI system is a system that can be modeled by a single first order...
, nondimensionalization can recover these values. The technique is especially useful for systems that can be described by differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. One important use is in the analysis of control system
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
s.
One of the simplest characteristic units is the doubling time
Doubling time
The doubling time is the period of time required for a quantity to double in size or value. It is applied to population growth, inflation, resource extraction, consumption of goods, compound interest, the volume of malignant tumours, and many other things which tend to grow over time...
of a system experiencing exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
, or conversely the half-life
Half-life
Half-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
of a system experiencing exponential decay; a more natural pair of characteristic units is mean age/mean lifetime, which correspond to base e rather than base 2.
Many illustrative examples of nondimensionalization originate from simplifying differential equations. This is because a large body of physical problems can be formulated in terms of differential equations. Consider the following:
- List of dynamical systems and differential equations topics
- List of partial differential equation topics
- Differential equations of mathematical physics
Although nondimensionalization is well adapted for these problems, it is not restricted to them. An example of a non-differential-equation application is dimensional analysis, while another is normalization
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
Measuring device
Measuring instrument
In the physical sciences, quality assurance, and engineering, measurement is the activity of obtaining and comparing physical quantities of real-world objects and events. Established standard objects and events are used as units, and the process of measurement gives a number relating the item...
s are practical examples of nondimensionalization occurring in everyday life. Measuring devices are calibrated relative to some known unit. Subsequent measurements are made relative to this standard. Then, the absolute value of the measurement is recovered by scaling with respect to the standard.
Rationale
Suppose a pendulumPendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
is swinging with a particular period
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
T. For such a system, it is advantageous to perform calculations relating to the swinging relative to T. In some sense, this is normalizing the measurement with respect to the period.
Measurements made relative to an intrinsic property of a system will apply to other systems which also have the same intrinsic property. It also allows one to compare a common property of different implementations of the same system. Nondimensionalization determines in a systematic manner the characteristic units of a system to use, without relying heavily on prior knowledge of the system's intrinsic properties
(one should not confuse characteristic units of a system with natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
of nature). In fact, nondimensionalization can suggest the parameters which should be used for analyzing a system. However, it is necessary to start with an equation that describes the system appropriately.
Nondimensionalization steps
To nondimensionalize a system of equations, one must do the following:- Identify all the independent and dependent variables;
- Replace each of them with a quantity scaled relative to a characteristic unit of measure to be determined;
- Divide through by the coefficient of the highest order polynomial or derivative term;
- Choose judiciously the definition of the characteristic unit for each variable so that the coefficients of as many terms as possible become 1;
- Rewrite the system of equations in terms of their new dimensionless quantities.
The last three steps are usually specific to the problem where nondimensionalization is applied. However, almost all systems require the first two steps to be performed.
As an illustrative example, consider a first order differential equation with constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
:
- In this equation the independent variable here is t, and the dependent variable is x.
- Set
 . This results in the equation
. This results in the equation
- The coefficient of the highest ordered term is in front of the first derivative term. Dividing by this gives
- The coefficient in front of χ only contains one characteristic variable tc, hence it is easiest to choose to set this to unity first:
 Subsequently,
Subsequently, 
- The final dimensionless equation in this case becomes completely independent of any parameters with units:
Substitutions
Suppose for simplicity that a certain system is characterized by two variables - a dependent variable x and an independent variable t, where x is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of t. Both x and t represent quantities with units. To scale these two variables, assume there are two intrinsic units of measurement xc and tc with the same units as x and t respectively, such that these conditions hold:


These equations are used to replace x and t when nondimensionalizing. If differential operators are needed to describe the original system, their scaled counterparts become dimensionless differential operators.
Conventions
There are no restrictions on the variable names used to replace "x" and "t". However, they are generally chosen so that it is convenient and intuitive to use for the problem at hand. For example, if "x" represented mass, the letter "m" might be an appropriate symbol to represent the dimensionless mass quantity.In this article, the following conventions have been used:
- t - represents the independent variable - usually a time quantity. Its nondimensionalized counterpart is τ.
- x - represents the dependent variable - can be mass, voltage, or any measurable quantity. Its nondimensionalized counterpart is χ.
A subscripted c added to a quantity's variable-name is used to denote the characteristic unit used to scale that quantity. For example, if x is a quantity, then xc is the characteristic unit used to scale it.
Differential operators
Consider the relationship
The dimensionless differential operators with respect to the independent variable becomes

Forcing function
If a system has a forcing functionForcing function (differential equations)
In a system of differential equations used to describe a time-dependent process, a forcing function is a function that appears in the equations and is only a function of time, not of any of the other variables. In effect, it is a constant for each value of t....
f(t), then

Hence, the new forcing function F is made to be dependent on the dimensionless quantity τ.
First order system
Let us consider the differential equation for a first order system:
The derivation of the characteristic units for this system gives

Second order system
A second order system has the form
Substitution step
Replace the variables x and t with their scaled quantities. The equation becomes
This new equation is not dimensionless, although all the variables with units are isolated in the coefficients. Dividing by the coefficient of the highest ordered term, the equation becomes

Now it is necessary to determine the quantities of xc and tc so that the coefficients become normalized. Since there are two free parameters, at most only two coefficients can be made to equal unity.
Determination of characteristic units
Consider the variable tc:- If
 the first order term is normalized.
the first order term is normalized. - If
 the zeroth order term is normalized.
the zeroth order term is normalized.
Both substitutions are valid. However, for pedagogical reasons, the latter substitution is used for second order systems. Choosing this substitution allows xc to be determined by normalizing the coefficient of the forcing function:

The differential equation becomes

The coefficient of the first order term is unitless. Define

The factor 2 is present so that the solutions can be parameterized in terms of ζ. In the context of mechanical or electrical systems, ζ is known as the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
, and is an important parameter required in the analysis of control system
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
s. 2ζ is also known as the linewidth of the system. The result of the definition is the universal oscillator equation.

Higher order systems
The general n-th order linear differential equation with constant coefficients has the form:
The function f(t) is known as the forcing function
Forcing function (differential equations)
In a system of differential equations used to describe a time-dependent process, a forcing function is a function that appears in the equations and is only a function of time, not of any of the other variables. In effect, it is a constant for each value of t....
.
If the differential equation only contains real (not complex) coefficients, then the properties of such a system behaves as a mixture of first and second order systems only. This is because the roots of its characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
are either real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, or complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
pairs. Therefore, understanding how nondimensionalization applies to first and second ordered systems allows the properties of higher order systems to be determined through superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
.
The number of free parameters in a nondimensionalized form of a system increases with its order. For this reason, nondimensionalization is rarely used for higher order differential equations. The need for this procedure has also been reduced with the advent of symbolic computation
Symbolic computation
Symbolic computation or algebraic computation, relates to the use of machines, such as computers, to manipulate mathematical equations and expressions in symbolic form, as opposed to manipulating the approximations of specific numerical quantities represented by those symbols...
.
Examples of recovering characteristic units
A variety of systems can be approximated as either first or second order systems. These include mechanical, electrical, fluidic, caloric, and torsional systems. This is because the fundamental physical quantities involved within each of these examples are related through first and second order derivatives.Mechanical oscillations

Define
- x = displacement from equilibrium [m]
- t = time [s]
- f = external force or "disturbance" applied to system [kg m s-2]
- m = mass of the block [kg]
- B = damping constant of dashpot [kg s-1]
- k = force constant of spring [kg s-2]
Suppose the applied force is a sinusoid F = F0 cos(ωt), the differential equation that describes the motion of the block is

Nondimensionalizing this equation the same way as described under second order system yields several characteristics of the system.
The intrinsic unit xc corresponds to the distance the block moves per unit force

The characteristic variable tc is equal to the period of the oscillations

and the dimensionless variable 2ζ corresponds to the linewidth of the system. ζ itself is the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
.

First-order series RC circuit
For a series RC
RC circuit
A resistor–capacitor circuit ', or RC filter or RC network, is an electric circuit composed of resistors and capacitors driven by a voltage or current source...
attached to a voltage source
Power supply
A power supply is a device that supplies electrical energy to one or more electric loads. The term is most commonly applied to devices that convert one form of electrical energy to another, though it may also refer to devices that convert another form of energy to electrical energy...

with substitutions

The first characteristic unit corresponds to the total charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
in the circuit. The second characteristic unit corresponds to the time constant
Time constant
In physics and engineering, the time constant, usually denoted by the Greek letter \tau , is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant system.Concretely, a first-order LTI system is a system that can be modeled by a single first order...
for the system.
Second-order series RLC circuit
For a series configuration of R,C,L components where Q is the charge in the system

with the substitutions

The first variable corresponds to the maximum charge stored in the circuit. The resonance frequency is given by the reciprocal of the characteristic time. The last expression is the linewidth of the system. The Ω can be considered as a normalized forcing function frequency.
Nonlinear differential equation example
Since there are no general methods of solving nonlinear differential equations, each case has to be considered on an individual basis when nondimensionalizing.Quantum harmonic oscillator
The Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for the one dimensional time independent quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
is

The modulus square of the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
|ψ|^2 represents probability, which is in a sense already dimensionless and normalized. Therefore, there is no need to nondimensionalize the wavefunction. However, it should be rewritten as a function of a dimensionless variable. Furthermore, the variable x has units of length. Hence substitute

The differential equation becomes

To make the term in front of χ² unitless, set

Hence, the fully nondimensionalized equation is

The nondimensionalization factor for the energy is the same as the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
of the harmonic oscillator. Usually, the energy term is not made dimensionless because a primary emphasis of quantum mechanics is determining the energies of the states of a system. Rearranging the first equation, the familiar equation for the harmonic oscillator is

Statistical analogs
In statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the analogous process is usually dividing a difference (a distance) by a scale factor (a measure of statistical dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
), which yields a dimensionless number, which is called normalization
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
. Most often, this is dividing errors or residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
by the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
or sample standard deviation, respectively, yielding standard score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
s and studentized residual
Studentized residual
In statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...
s.
See also
- Buckingham π theorem
- Dimensional analysisDimensional analysisIn physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
- Dimensionless number
- Natural unitsNatural unitsIn physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
- List of dynamical systems and differential equations topics
- List of partial differential equation topics
- Differential equations of mathematical physics
- System equivalenceSystem equivalenceIn the systems sciences the term system equivalence is the notion that a parameter or component of a system behaves in a similar way as a parameter or component of a different system. Similarity means that mathematically the parameters/components will be indistinguishable from each other...
- RLC circuitRLC circuitAn RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...
- RL circuitRL circuitA resistor-inductor circuit ', or RL filter or RL network, is one of the simplest analogue infinite impulse response electronic filters. It consists of a resistor and an inductor, either in series or in parallel, driven by a voltage source.-Introduction:The fundamental passive linear circuit...
- RC circuitRC circuitA resistor–capacitor circuit ', or RC filter or RC network, is an electric circuit composed of resistors and capacitors driven by a voltage or current source...
- Logistic equation
- Normalization (statistics)Normalization (statistics)In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
External links
- Analysis of differential equation models in biology: a case study for clover meristem populations (Application of nondimensionalization to a problem in biology).
- Course notes for Mathematical Modelling and Industrial Mathematics Jonathan Evans, Department of Mathematical Sciences, University of BathUniversity of BathThe University of Bath is a campus university located in Bath, United Kingdom. It received its Royal Charter in 1966....
. (see Chapter 3).





