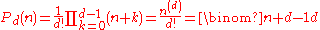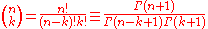Pascal's triangle
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Pascal's triangle is a triangular array
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s in a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. It is named after the French mathematician, Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
. It is known as Pascal's triangle in much of the Western world
Western world
The Western world, also known as the West and the Occident , is a term referring to the countries of Western Europe , the countries of the Americas, as well all countries of Northern and Central Europe, Australia and New Zealand...
, although other mathematicians studied it centuries before him in India
History of India
The history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
, Persia
History of Iran
The history of Iran has been intertwined with the history of a larger historical region, comprising the area from the Danube River in the west to the Indus River and Jaxartes in the east and from the Caucasus, Caspian Sea, and Aral Sea in the north to the Persian Gulf and the Gulf of Oman and Egypt...
, China
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Germany
History of Germany
The concept of Germany as a distinct region in central Europe can be traced to Roman commander Julius Caesar, who referred to the unconquered area east of the Rhine as Germania, thus distinguishing it from Gaul , which he had conquered. The victory of the Germanic tribes in the Battle of the...
, and Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
.
The rows of Pascal's triangle are conventionally enumerated starting with row n = 0 at the top. The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. A simple construction of the triangle proceeds in the following manner. On row 0, write only the number 1. Then, to construct the elements of following rows, add the number directly above and to the left with the number directly above and to the right to find the new value. If either the number to the right or left is not present, substitute a zero in its place. For example, the first number in the first row is 0 + 1 = 1, whereas the numbers 1 and 3 in the third row are added to produce the number 4 in the fourth row.
This construction is related to the binomial coefficients by Pascal's rule, which says that if
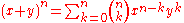
then
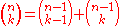
for any nonnegative integer n and any integer k between 0 and n.
Pascal's triangle has higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al generalizations. The three-dimensional version is called Pascal's pyramid
Pascal's pyramid
In mathematics, Pascal's Pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution. Pascal's Pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial...
or Pascal's tetrahedron, while the general versions are called Pascal's simplices
Pascal's simplex
In mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.- Induction of Pascal's simplices :...
.
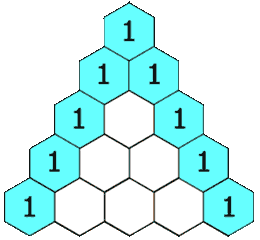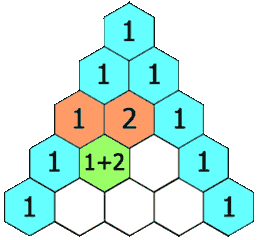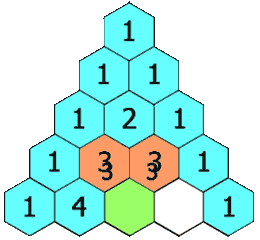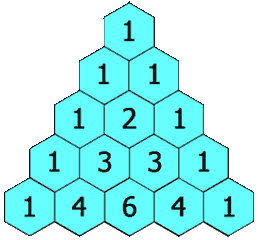
History

Treatise
A treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
, Traité du triangle arithmétique (1653). The numbers originally arose from Hindu studies of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and binomial numbers and the Greeks
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
' study of figurate numbers.
The earliest explicit depictions of a triangle of binomial coefficients occur in the 10th century in commentaries on the Chandas Shastra, an Ancient Indian
History of India
The history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
book on Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
prosody written by Pingala
Pingala
Pingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...
in or before the 2nd century BC. While Pingala's work only survives in fragments, the commentator Halayudha
Halayudha
Halayudha was a 10th century Indian mathematician who wrote the ', a commentary on Pingala's Chandah-shastra, containing a clear description of Pascal's triangle ....
, around 975, used the triangle to explain obscure references to Meru-prastaara, the "Staircase of Mount Meru". It was also realised that the shallow diagonals of the triangle sum to the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s. In 1068, four columns of the first sixteen rows were given by the mathematician Bhattotpala, who realized the combinatorial significance.
At around the same time, it was discussed in Persia
History of Iran
The history of Iran has been intertwined with the history of a larger historical region, comprising the area from the Danube River in the west to the Indus River and Jaxartes in the east and from the Caucasus, Caspian Sea, and Aral Sea in the north to the Persian Gulf and the Gulf of Oman and Egypt...
(Iran) by the Persian mathematician, Al-Karaji
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
(953–1029). It was later repeated by the Persian poet-astronomer-mathematician Omar Khayyám
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
(1048–1131); thus the triangle is referred to as the Khayyam-Pascal triangle or simply the Khayyam triangle in Iran. Several theorems related to the triangle were known, including the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. Khayyam used a method of finding nth roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
based on the binomial expansion, and therefore on the binomial coefficients.
In 13th century, Yang Hui
Yang Hui
Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
(1238–1298) presented the arithmetic triangle that is the same as Pascal's triangle. Pascal's triangle is called Yang Hui's triangle in China
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
. The "Yang Hui's triangle" was known in China in the early 11th century by the Chinese mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
(1010-1070).
Petrus Apianus
Petrus Apianus
Petrus Apianus , also known as Peter Apian, was a German humanist, known for his works in mathematics, astronomy and cartography.The lunar crater Apianus and minor planet 19139 Apian are named in his honour....
(1495–1552) published the triangle on the frontispiece
Book frontispiece
A frontispiece is a decorative illustration facing a book's title page. The frontispiece is the verso opposite the recto title page. Elaborate engraved frontispieces were in frequent use, especially in Bibles and in scholarly books, and many are masterpieces of engraving...
of his book on business calculations in the 16th century. This is the first record of the triangle in Europe.
In Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
, it is referred to as Tartaglia's triangle, named for the Italian algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ist Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
(1500–77). Tartaglia is credited with the general formula for solving cubic polynomials, (which may in fact be from Scipione del Ferro
Scipione del Ferro
Scipione del Ferro was an Italian mathematician who first discovered a method to solve the depressed cubic equation.-Life:Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro...
but was published by Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
1545).
Pascal's Traité du triangle arithmétique (Treatise on Arithmetical Triangle) was published posthumously in 1665. In this, Pascal collected several results then known about the triangle, and employed them to solve problems in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. The triangle was later named after Pascal by Pierre Raymond de Montmort
Pierre Raymond de Montmort
Pierre Rémond de Montmort, a French mathematician, was born in Paris on 27 October 1678, and died there on 7 October 1719. His name was originally just Pierre Rémond or Raymond...
(1708) who called it "Table de M. Pascal pour les combinaisons" (French: Table of Mr. Pascal for combinations) and Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
(1730) who called it "Triangulum Arithmeticum PASCALIANUM" (Latin: Pascal's Arithmetic Triangle), which became the modern Western name.
Binomial expansions
Pascal's triangle determines the coefficients which arise in binomial expansions. For an example, consider the expansion2 = x2 + 2xy + y2 = 1x2y0 + 2x1y1 + 1x0y2.
Notice the coefficients are the numbers in row two of Pascal's triangle: 1, 2, 1.
In general, when a binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
like x + y is raised to a positive integer power we have:
n = a0xn + a1xn−1y + a2xn−2y2 + ... + an−1xyn−1 + anyn,
where the coefficients ai in this expansion are precisely the numbers on row n of Pascal's triangle. In other words,
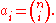
This is the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
.
Notice that the entire right diagonal of Pascal's triangle corresponds to the coefficient of yn in these binomial expansions, while the next diagonal corresponds to the coefficient of xyn−1 and so on.
To see how the binomial theorem relates to the simple construction of Pascal's triangle, consider the problem of calculating the coefficients of the expansion of (x + 1)n+1 in terms of the corresponding coefficients of (x + 1)n (setting y = 1 for simplicity). Suppose then that
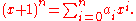
Now
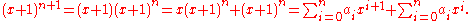
The two summations can be reorganized as follows:

(because of how raising a polynomial to a power works, a0 = an = 1).
We now have an expression for the polynomial (x + 1)n+1 in terms of the coefficients of (x + 1)n (these are the ais), which is what we need if we want to express a line in terms of the line above it. Recall that all the terms in a diagonal going from the upper-left to the lower-right correspond to the same power of x, and that the a-terms are the coefficients of the polynomial (x + 1)n, and we are determining the coefficients of (x + 1)n+1. Now, for any given i not 0 or n + 1, the coefficient of the xi term in the polynomial (x + 1)n+1 is equal to ai (the figure above and to the left of the figure to be determined, since it is on the same diagonal) + ai−1 (the figure to the immediate right of the first figure). This is indeed the simple rule for constructing Pascal's triangle row-by-row.
It is not difficult to turn this argument into a proof (by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
) of the binomial theorem. Since
(a + b)n = bn(a/b + 1)n, the coefficients are identical in the expansion of the general case.
An interesting consequence of the binomial theorem is obtained by setting both variables x and y equal to one. In this case, we know that (1 + 1)n = 2n, and so

In other words, the sum of the entries in the nth row of Pascal's triangle is the nth power of 2.
Combinations
A second useful application of Pascal's triangle is in the calculation of combinationCombination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s. For example, the number combinations of n things taken k at a time (called n choose k) can be found by the equation

But this is also the formula for a cell of Pascal's triangle. Rather than performing the calculation, one can simply look up the appropriate entry in the triangle. For example, suppose a basketball team has 10 players and wants to know how many ways there are of selecting 8. Provided we have the first row and the first entry in a row numbered 0, the answer is entry 8 in row 10: 45. That is, the solution of 10 choose 8 is 45.
Relation to binomial distribution and convolutions
When divided by 2n, the nth row of Pascal's triangle becomes the binomial distribution in the symmetric case where p = 1/2. By the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, this distribution approaches the normal distribution as n increases. This can also be seen by applying Stirling's formula to the factorials involved in the formula for combinations.
This is related to the operation of discrete convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
in two ways. First, polynomial multiplication exactly corresponds to discrete convolution, so that repeatedly convolving the sequence {..., 0, 0, 1, 1, 0, 0, ...} with itself corresponds to taking powers of 1 + x, and hence to generating the rows of the triangle. Second, repeatedly convolving the distribution function for a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with itself corresponds to calculating the distribution function for a sum of n independent copies of that variable; this is exactly the situation to which the central limit theorem applies, and hence leads to the normal distribution in the limit.
Patterns and properties
Pascal's triangle has many properties and contains many patterns of numbers.Rows
- When adding all the digits in a single row, each successive row has twice the value of the row preceding it. For example, row 1 has a value of 1, row 2 has a value of 2, row 3 has a value of 4, and so forth.
- The value of a row, if each entry is considered a decimal place (and numbers larger than 9 carried over accordingly) is a power of 11 ( 11n, for row n). Thus, in row two, '1,2,1' becomes 112, while '1,5,10,10,5,1' in row five becomes (after carrying) 161,051, which is 115. This property is explained by setting x = '10' in the binomial expansion of (x + 1)row=n, and adjusting values to the decimal system. But x can be chosen to allow rows to represent values in any base - such as base 3; 1 2 13 ['1,2,1'] = 42 (16), 2 1 0 13 ['1,3,3,1'] = 43 (64) - or base 9; 1 2 19 = 102 (100), 1 3 3 19 = 103 (1000) and 1 6 2 1 5 19 ['1,5,10,10,5,1'] = 105 (100,000). In particular (see next property), for x = 1 place value remains constant (1place=1). Thus entries can simply be added in interpreting the value of a row.
- The sum of the elements of row m is equal to 2m−1. For example, the sum of the elements of row 5 is 1 + 4 + 6 + 4 + 1 = 16, which is equal to 24 = 16. This follows from the binomial theorem proved above, applied to (1 + 1)m−1.
- If rows are numbered starting with n = 0, the sum of the elements in the row is simply 2n, so row 0 adds to 20 = 1, row 1 adds to 21 = 2, etc.
- Some of the numbers in Pascal's triangle correlate to numbers in Lozanić's triangleLozanic's triangleLozanić's triangle is a triangular array of binomial coefficients in a manner very similar to that of Pascal's triangle...
. - The sum of the squares of the elements of row n equals the middle element of row (2n − 1). For example, 12 + 42 + 62 + 42 + 12 = 70. In general form:
-
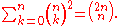
- Another interesting pattern is that on any row m, where m is odd, the middle term minus the term two spots to the left equals a Catalan numberCatalan numberIn combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
, specifically the (m + 1)/2 Catalan number. For example: on row 5, 6 − 1 = 5, which is the 3rd Catalan number, and (5 + 1)/2 = 3. - Another interesting property of Pascal's triangle is that in rows where the second number (immediately following '1') is prime, all the terms in that row except the 1s are multiples of that prime.
- Another interesting pattern is that on any row m, where m is odd, the middle term minus the term two spots to the left equals a Catalan number
- Parity: Start numbering the row from 0. To count odd terms in nth row, convert n to binary. Let x be the number of 1s in the binary representation. Then number of odd terms will be 2x.
Diagonals
The diagonals of Pascal's triangle contain the figurate numbers of simplices:- The diagonals going along the left and right edges contain only 1's.
- The diagonals next to the edge diagonals contain the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s in order. - Moving inwards, the next pair of diagonals contain the triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s in order. - The next pair of diagonals contain the tetrahedral numberTetrahedral numberA tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
s in order, and the next pair give pentatope numberPentatope numberA pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.The first few numbers of this kind are :...
s.
-

The symmetry of the triangle implies that the nth d-dimensional number is equal to the dth n-dimensional number.
An alternative formula that does not involve recursion is as follows:
- where n(d) is the rising factorialPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
.
The geometric meaning of a function Pd is: Pd(1) = 1 for all d. Construct a d-dimensional triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
(a 3-dimensional triangle is a tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
) by placing additional dots below an initial dot, corresponding to Pd(1) = 1. Place these dots in a manner analogous to the placement of numbers in Pascal's triangle. To find Pd(x), have a total of x dots composing the target shape. Pd(x) then equals the total number of dots in the shape. A 0-dimensional triangle is a point and a 1-dimensional triangle is simply a line, and therefore P0(x) = 1 and P1(x) = x, which is the sequence of natural numbers. The number of dots in each layer corresponds to Pd − 1(x).
Calculating an individual row or diagonal by itself
This algorithm is an alternative to the standard method of calculating individual cells with factorials. Starting at the left, the first cell's value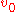 is 1. For each cell after, the value is determined by multiplying the value to its left by a slowly changing fraction:
is 1. For each cell after, the value is determined by multiplying the value to its left by a slowly changing fraction:
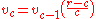
where r = row + 1, starting with 0 at the top, and c = the column, starting with 0 on the left. For example, to calculate row 5, r = 6. The first value is 1. The next value is 1 × 5/1 = 5. The numerator decreases by one, and the denominator increases by one with each step. So 5 × 4/2 = 10. Then 10 × 3/3 = 10. Then 10 × 2/4 = 5. Then 5 × 1/5 = 1. Notice that the last cell always equals 1, the final multiplication is included for completeness of the series.
A similar pattern exists on a downward diagonal. Starting with the one and the natural number in the next cell, form a fraction. To determine the next cell, increase the numerator and denominator each by one, and then multiply the previous result by the fraction. For example, the row starting with 1 and 7 form a fraction of 7/1. The next cell is 7 × 8/2 = 28. The next cell is 28 × 9/3 = 84. (Note that for any individual row it is only necessary to calculate half (rounded up) the terms in the row due to symmetry.)
Overall patterns and properties

- The pattern obtained by coloring only the odd numbers in Pascal's triangle closely resembles the fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
called the Sierpinski triangleSierpinski triangleThe Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
. This resemblance becomes more and more accurate as more rows are considered; in the limit, as the number of rows approaches infinity, the resulting pattern is the Sierpinski triangle, assuming a fixed perimeter. More generally, numbers could be colored differently according to whether or not they are multiples of 3, 4, etc.; this results in other similar patterns.
- Imagine each number in the triangle is a node in a grid which is connected to the adjacent numbers above and below it. Now for any node in the grid, count the number of paths there are in the grid (without backtracking) which connect this node to the top node (1) of the triangle. The answer is the Pascal number associated to that node. The interpretation of the number in Pascal's Triangle as the number of paths to that number from the tip means that on a PlinkoPlinkoPlinko is a pricing game on the American television game show The Price Is Right. The game involves guessing the prices of prizes to win "Plinko chips," which are later dropped down a large bean machine-style board to determine the contestant's cash prize...
game board shaped like a triangle, the probability of winning prizes nearer the center will be higher than winning prizes on the edges.
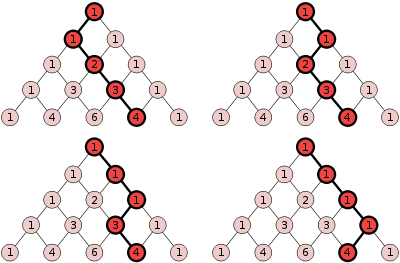
- One property of the triangle is revealed if the rows are left-justified. In the triangle below, the diagonal coloured bands sum to successive Fibonacci numberFibonacci numberIn mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
-
- {| style="align:center;"
|- align=center
|bgcolor=red|1
|- align=center
| style="background:orange;"|1
| style="background:yellow;"|1
|- align=center
| style="background:yellow;"|1
|bgcolor=lime|2
|bgcolor=aqua|1
|- align=center
|bgcolor=lime|1
|bgcolor=aqua|3
| style="background:violet;"|3
|bgcolor=red|1
|- align=center
|bgcolor=aqua|1
| style="background:violet;"|4
|bgcolor=red|6
| style="background:orange;"|4
| style="background:yellow;"|1
|- align=center
| style="background:violet;"|1
|bgcolor=red|5
| style="background:orange;"|10
| style="background:yellow;"|10
|bgcolor=lime|5
|bgcolor=aqua|1
|- align=center
|bgcolor=red|1
| style="background:orange;"|6
| style="background:yellow;"|15
|bgcolor=lime|20
|bgcolor=aqua|15
| style="background:violet;"|6
|bgcolor=red|1
|- align=center
| style="background:orange;"|1
| style="background:yellow;"|7
|bgcolor=lime|21
|bgcolor=aqua|35
| style="background:violet;"|35
|bgcolor=red|21
| style="background:orange;"|7
| style="background:yellow;"|1
|- align=center
| style="background:yellow; width:50px;"|1
| style="background:lime; width:50px;"|8
| style="background:aqua; width:50px;"|28
| style="background:violet; width:50px;"|56
| style="background:red; width:50px;"|70
| style="background:orange; width:50px;"|56
| style="background:yellow; width:50px;"|28
| style="background:lime; width:50px;"|8
| style="background:aqua; width:50px;"|1
|}
Construction as matrix exponential

Due to its simple construction by factorials, a very basic representation of Pascal's triangle in terms of the matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
can be given: Pascal's triangle is the exponential of the matrix which has the sequence 1, 2, 3, 4, … on its subdiagonal and zero everywhere else.
Number of elements of polytopes
Pascal's triangle can be used as a lookup tableLookup tableIn computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
for the number of elements (such as edges and corners) within a polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
(such as a triangle, a tetrahedron, a square and a cube).
Let's begin by considering the 3rd line of Pascal's triangle, with values 1, 3, 3, 1. A 2-dimensional triangle has one 2-dimensional element (itself), three 1-dimensional elements (lines, or edges), and three 0-dimensional elements (verticesVertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, or corners). The meaning of the final number (1) is more difficult to explain (but see below). Continuing with our example, a tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
has one 3-dimensional element (itself), four 2-dimensional elements (faces), six 1-dimensional elements (edges), and four 0-dimensional elements (vertices). Adding the final 1 again, these values correspond to the 4th row of the triangle (1, 4, 6, 4, 1). Line 1 corresponds to a point, and Line 2 corresponds to a line segment (dyad). This pattern continues to arbitrarily high-dimensioned hyper-tetrahedrons (known as simplicesSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
).
To understand why this pattern exists, one must first understand that the process of building an n-simplex from an (n − 1)-simplex consists of simply adding a new vertex to the latter, positioned such that this new vertex lies outside of the space of the original simplex, and connecting it to all original vertices. As an example, consider the case of building a tetrahedron from a triangle, the latter of whose elements are enumerated by row 3 of Pascal's triangle: 1 face, 3 edges, and 3 vertices (the meaning of the final 1 will be explained shortly). To build a tetrahedron from a triangle, we position a new vertex above the plane of the triangle and connect this vertex to all three vertices of the original triangle.
The number of a given dimensional element in the tetrahedron is now the sum of two numbers: first the number of that element found in the original triangle, plus the number of new elements, each of which is built upon elements of one fewer dimension from the original triangle. Thus, in the tetrahedron, the number of cells (polyhedral elements) is 0 (the original triangle possesses none) + 1 (built upon the single face of the original triangle) = 1; the number of faces is 1 (the original triangle itself) + 3 (the new faces, each built upon an edge of the original triangle) = 4; the number of edges is 3 (from the original triangle) + 3 (the new edges, each built upon a vertex of the original triangle) = 6; the number of new vertices is 3 (from the original triangle) + 1 (the new vertex that was added to create the tetrahedron from the triangle) = 4. This process of summing the number of elements of a given dimension to those of one fewer dimension to arrive at the number of the former found in the next higher simplex is equivalent to the process of summing two adjacent numbers in a row of Pascal's triangle to yield the number below. Thus, the meaning of the final number (1) in a row of Pascal's triangle becomes understood as representing the new vertex that is to be added to the simplex represented by that row to yield the next higher simplex represented by the next row. This new vertex is joined to every element in the original simplex to yield a new element of one higher dimension in the new simplex, and this is the origin of the pattern found to be identical to that seen in Pascal's triangle.
A similar pattern is observed relating to squaresSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, as opposed to triangles. To find the pattern, one must construct an analog to Pascal's triangle, whose entries are the coefficients of (x + 2)Row Number, instead of (x + 1)Row Number. There are a couple ways to do this. The simpler is to begin with Row 0 = 1 and Row 1 = 1, 2. Proceed to construct the analog triangles according to the following rule:
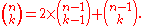
That is, choose a pair of numbers according to the rules of Pascal's triangle, but double the one on the left before adding. This results in:
1
1 2
1 4 4
1 6 12 8
1 8 24 32 16
1 10 40 80 80 32
1 12 60 160 240 192 64
1 14 84 280 560 672 448 128
The other way of manufacturing this triangle is to start with Pascal's triangle and multiply each entry by 2k, where k is the position in the row of the given number. For example, the 2nd value in row 4 of Pascal's triangle is 6 (the slope of 1s corresponds to the zeroth entry in each row). To get the value that resides in the corresponding position in the analog triangle, multiply 6 by 2Position Number = 6 × 22 = 6 × 4 = 24. Now that the analog triangle has been constructed, the number of elements of any dimension that compose an arbitrarily dimensioned cube (called a hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
) can be read from the table in a way analogous to Pascal's triangle. For example, the number of 2-dimensional elements in a 2-dimensional cube (a square) is one, the number of 1-dimensional elements (sides, or lines) is 4, and the number of 0-dimensional elements (points, or vertices) is 4. This matches the 2nd row of the table (1, 4, 4). A cube has 1 cube, 6 faces, 12 edges, and 8 vertices, which corresponds to the next line of the analog triangle (1, 6, 12, 8). This pattern continues indefinitely.
To understand why this pattern exists, first recognize that the construction of an n-cube from an (n − 1)-cube is done by simply duplicating the original figure and displacing it some distance (for a regular n-cube, the edge length) orthogonal to the space of the original figure, then connecting each vertex of the new figure to its corresponding vertex of the original. This initial duplication process is the reason why, to enumerate the dimensional elements of an n-cube, one must double the first of a pair of numbers in a row of this analog of Pascal's triangle before summing to yield the number below. The initial doubling thus yields the number of "original" elements to be found in the next higher n-cube and, as before, new elements are built upon those of one fewer dimension (edges upon vertices, faces upon edges, etc.). Again, the last number of a row represents the number of new vertices to be added to generate the next higher n-cube.
In this triangle, the sum of the elements of row m is equal to 3m − 1. Again, to use the elements of row 5 as an example: , which is equal to
, which is equal to  .
.
Fourier transform of sin(x)n+1/x
As stated previously, the coefficients of (x + 1)n are the nth row of the triangle. Now the coefficients of (x − 1)n are the same, except that the sign alternates from +1 to −1 and back again. After suitable normalization, the same pattern of numbers occurs in the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of sin(x)n+1/x. More precisely: if n is even, take the real part of the transform, and if n is odd, take imaginary part. Then the result is a step functionStep functionIn mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
, whose values (suitably normalized) are given by the nth row of the triangle with alternating signs. For example, the values of the step function that results from

compose the 4th row of the triangle, with alternating signs. This is a generalization of the following basic result (often used in electrical engineeringElectrical engineeringElectrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
):

is the boxcar functionBoxcar functionIn mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...
. The corresponding row of the triangle is row 0, which consists of just the number 1.
If n is congruentCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to 2 or to 3 mod 4, then the signs start with −1. In fact, the sequence of the (normalized) first terms corresponds to the powers of iImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, which cycle around the intersection of the axes with the unit circle in the complex plane:
Elementary cellular automaton
The pattern produced by an elementary cellular automatonElementary cellular automatonIn mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors....
using rule 60 is exactly Pascal's triangle of binomial coefficients reduced modulo 2 (black cells correspond to odd binomial coefficients). Rule 102 also produces this pattern when trailing zeros are omitted. Rule 90Rule 90Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value; in each time step all values are simultaneously replaced by the exclusive or of the two neighboring values...
produces the same pattern but with an empty cell separating each entry in the rows.
Extensions
Pascal's Triangle can be extended to negative row numbers.
First write the triangle in the following form:
m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ... n = 0 1 0 0 0 0 0 ... n = 1 1 1 0 0 0 0 ... n = 2 1 2 1 0 0 0 ... n = 3 1 3 3 1 0 0 ... n = 4 1 4 6 4 1 0 ...
Next, extend the column of 1s upwards:
m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ... n = -4 1 ... n = -3 1 ... n = -2 1 ... n = -1 1 ... n = 0 1 0 0 0 0 0 ... n = 1 1 1 0 0 0 0 ... n = 2 1 2 1 0 0 0 ... n = 3 1 3 3 1 0 0 ... n = 4 1 4 6 4 1 0 ...
Now the rule:

can be rearranged to:
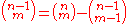
which allows calculation of the other entries for negative rows:
m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ... n = −4 1 −4 10 −20 35 −56 ... n = −3 1 −3 6 −10 15 −21 ... n = −2 1 −2 3 −4 5 −6 ... n = −1 1 −1 1 −1 1 −1 ... n = 0 1 0 0 0 0 0 ... n = 1 1 1 0 0 0 0 ... n = 2 1 2 1 0 0 0 ... n = 3 1 3 3 1 0 0 ... n = 4 1 4 6 4 1 0 ...
This extension preserves the property that the values in the mth column viewed as a function of n are fit by an order m polynomial, namely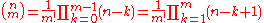 .
.
This extension also preserves the property that the values in the nth row correspond to the coefficients of :
:
For example: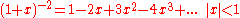
Another option for extending Pascal's triangle to negative rows comes from extending the other line of 1s:m = -4 m = -3 m = -2 m = -1 m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ... n = -4 1 0 0 0 0 0 0 0 0 0 ... n = -3 1 0 0 0 0 0 0 0 0 ... n = -2 1 0 0 0 0 0 0 0 ... n = -1 1 0 0 0 0 0 0 ... n = 0 0 0 0 0 1 0 0 0 0 0 ... n = 1 0 0 0 0 1 1 0 0 0 0 ... n = 2 0 0 0 0 1 2 1 0 0 0 ... n = 3 0 0 0 0 1 3 3 1 0 0 ... n = 4 0 0 0 0 1 4 6 4 1 0 ...
Applying the same rule as before leads tom = -4 m = -3 m = -2 m = -1 m = 0 m = 1 m = 2 m = 3 m = 4 m = 5 ... n = -4 1 0 0 0 0 0 0 0 0 0 ... n = -3 -3 1 0 0 0 0 0 0 0 0 ... n = -2 3 -2 1 0 0 0 0 0 0 0 ... n = -1 -1 1 -1 1 0 0 0 0 0 0 .. n = 0 0 0 0 0 1 0 0 0 0 0 ... n = 1 0 0 0 0 1 1 0 0 0 0 ... n = 2 0 0 0 0 1 2 1 0 0 0 ... n = 3 0 0 0 0 1 3 3 1 0 0 ... n = 4 0 0 0 0 1 4 6 4 1 0 ...
Note that this extension also has the properties that just as ,
,
we have

Also, just as summing along the lower-left to upper-right diagonals of the Pascal matrix yields the Fibonacci numbers, this second type of extension still sums to the Fibonacci numbers for negative index.
Either of these extensions can be reached if we define
and take certain limits of the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, .
.
See also
- Bean machineBean machineThe bean machine, also known as the quincunx or Galton box, is a device invented by Sir Francis Galton to demonstrate the central limit theorem, in particular that the normal distribution is approximate to the binomial distribution....
, Francis Galton's "quincunx" - Binomial expansion
- Euler triangle
- Floyd's triangleFloyd's triangleFloyd's triangle is a right-angled triangular array of natural numbers, used in computer science education. It is named after Robert Floyd. It is defined by filling the rows of the triangle with consecutive numbers, starting with a 1 in the top left corner:1...
- Leibniz harmonic triangleLeibniz harmonic triangleThe Leibniz harmonic triangle is a triangular arrangement of fractions in which the outermost diagonals consist of the reciprocals of the row numbers and each inner cell is the absolute value of the cell above minus the cell to the left...
- Multiplicities of entries in Pascal's triangleMultiplicities of entries in Pascal's triangleIn combinatorial number theory, Singmaster's conjecture, named after David Singmaster, says there is a finite upper bound on the multiplicities of entries in Pascal's triangle...
(Singmaster's conjecture) - Pascal matrixPascal matrixIn mathematics, particularly matrix theory and combinatorics, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. There are three ways to achieve this: as either an upper-triangular matrix, a lower-triangular matrix, or a symmetric matrix...
- Pascal's tetrahedron
- Pascal's simplexPascal's simplexIn mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.- Induction of Pascal's simplices :...
- Proton NMRProton NMRProton NMR is the application of nuclear magnetic resonance in NMR spectroscopy with respect to hydrogen-1 nuclei within the molecules of a substance, in order to determine the structure of its molecules. In samples where natural hydrogen is used, practically all of the hydrogen consists of the...
, one application of Pascal's triangle - Star of David theoremStar of David theoremThe Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by H.W. Gould in 1972.- Statement :...
- Trinomial expansion
External links
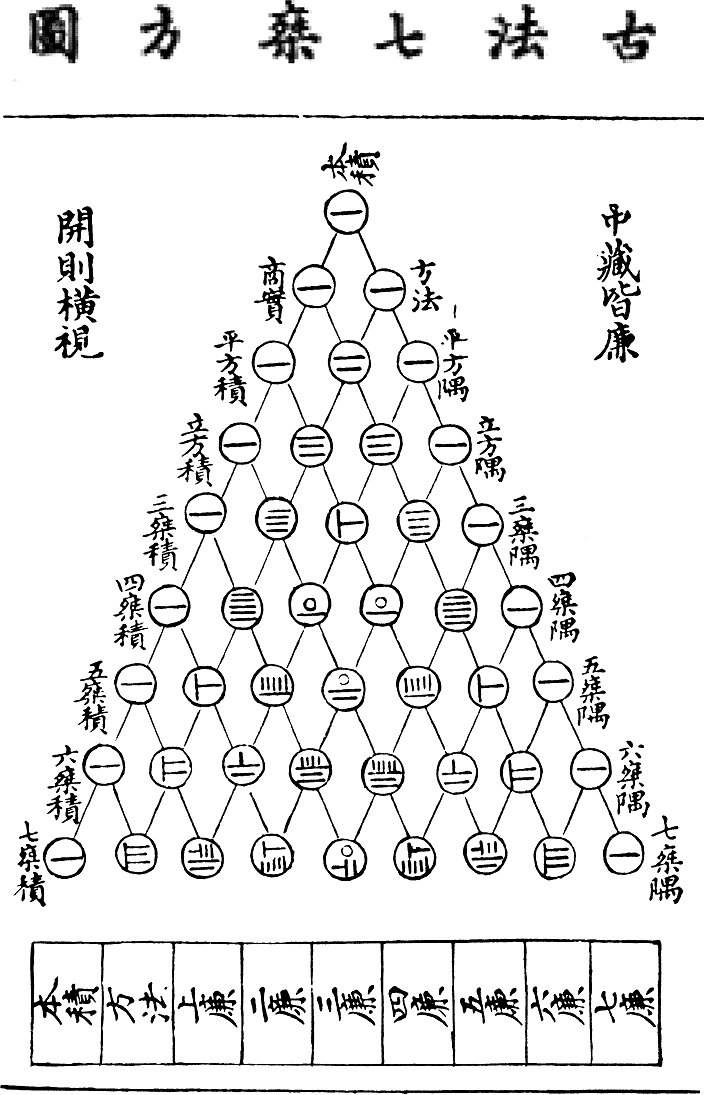
- The Old Method Chart of the Seven Multiplying Squares (from the Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303, depicting the first nine rows of Pascal's triangle)
- Implementation of Pascal Triangle in Java – with conversion of higher digits to single digits.
- Pascal's Treatise on the Arithmetic Triangle (page images of Pascal's treatise, 1655; summary)
- Earliest Known Uses of Some of the Words of Mathematics (P)
- Leibniz and Pascal triangles
- Dot Patterns, Pascal's Triangle, and Lucas' Theorem
- Omar Khayyam the mathematician
- Info on Pascal's Triangle
- Explanation of Pascal's Triangle and common occurrences, including link to interactive version specifying # of rows to view
- Implementation of Pascal Triangle in SQL
-