
Triangular number
Encyclopedia
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural number
s from 1 to n. The sequence of triangular numbers is:
The triangle numbers are given by the following explicit formulas:
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s from 1 to n. The sequence of triangular numbers is:
- 1, 3, 6, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 1515 (number)15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 2121 (number)21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 2828 (number)28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14....
, 3636 (number)36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number...
, 4545 (number)45 is the natural number following 44 and followed by 46.- In mathematics :Forty-five is a triangular number, a hexagonal and 16-gonal number, a Kaprekar number, and a Harshad number....
, 5555 (number)55 is the natural number following 54 and preceding 56.-Albania:*Gazeta 55, a newspaper*Constitution law 55, a law during Communist Albania.-Mathematics:...
, ....
The triangle numbers are given by the following explicit formulas:
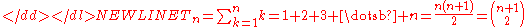
The rightmost expression, consisting of "n + 1" and "2" within parentheses, is a binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. It represents the number of distinct pairs that can be selected from n + 1 objects, and it is read aloud as "n plus one choose two". In this form, the triangular number Tn solves the handshake problem of counting the number of handshakes if each person in a room full of n + 1 total people shakes hands once with each other person.
Triangle numbers are the additive analog of the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s, which are the products of integers from 1 to n.
The number of lines you can draw between each of the dots can be represented with the following recurrence relation:

The ratio between the two numbers, dots and lines also has the interesting property of:
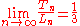
Relations to other figurate numbers
Triangular numbers have a wide variety of relations to other figurate numberFigurate numberThe term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...
s.
Most simply, the sum of two consecutive triangular numbers is a square numberSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, with the sum being the square of the difference between the two. Algebraically,
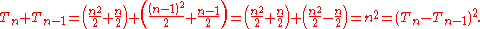
Alternatively, the same fact can be demonstrated graphically:6 + 10 = 16 
10 + 15 = 25 
There are infinitely many triangular numbers that are also square numbers; e.g., 1, 36. Some of them can be generated by a simple recursive formula:
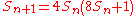 with
with 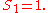
All square triangular numberSquare triangular numberIn mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
s are found from the recursion
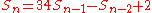 with
with 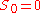 and
and 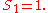
Also, the square of the nth triangular number is the same as the sum of the cubes of the integers 1 to n.
The sum of the all triangular numbers up to the nth triangular number is the nth tetrahedral numberTetrahedral numberA tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
,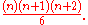
More generally, the difference between the nth m-gonal numberPolygonal numberIn mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
and the nth (m + 1)-gonal number is the (n - 1)th triangular number. For example, the sixth heptagonal number (81) minus the sixth hexagonal numberHexagonal numberA hexagonal number is a figurate number. The nth hexagonal number will be the number of points in a hexagon with n regularly spaced points on a side.The formula for the nth hexagonal number...
(66) equals the fifth triangular number, 15. Every other triangular number is a hexagonal number. Knowing the triangular numbers, one can reckon any centered polygonal numberCentered numberThe centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers with a constant number of sides...
: the nth centered k-gonal number is obtained by the formula
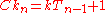
where T is a triangular number.
The positive difference of two triangular numbers is a trapezoidal number.
Other properties
Triangular numbers correspond to the 1st-order case of Faulhaber's formula.
Every even perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
is triangular, given by the formula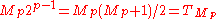
- where Mp is a Mersenne primeMersenne primeIn mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
. No odd perfect numbers are known, hence all known perfect numbers are triangular. - For example, the 3rd triangular number is 3x2 = 6; the 7th is 7x4 = 28; the 31st is 31x16 = 496; and the 127th is 127x64 = 8128.
In base 10, the digital rootDigital rootThe digital root of a number is the value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum...
of a triangular number is always 1, 3, 6, or 9. Hence every triangular number is either divisible by three or has a remainder of 1 when divided by nine:- 1 = 9×0+1,
- 3 = 3×1,
- 6 = 3×2,
- 10 = 9×1+1,
- 15 = 3×5,
- 21 = 3×7,
- 28 = 9×3+1,
- 36 = 9×4,
- 45 = 9×5,
- 55 = 9×6+1,
- ...
- The digital root pattern, repeating every nine terms, is "1 3 6 1 6 3 1 9 9".
The inverse of the statement above is, however, not always true. For example, the digital root of 12, which is not a triangular number, is 3 and divisible by three.
If x is a triangular number, then ax+b is also a triangular number, given the following conditions are satisfied:
a=an odd square, b=(a-1)/8
Note that b will always be a triangular number, because 8Tn+1=(2n+1)2, which yields all the odd squares are revealed by multiplying a triangular number by 8 and adding 1, and the process for b given a is an odd square is the inverse of this operation.
The first several pairs of this form (not counting 1x+0) are: 9x+1, 25x+3, 49x+6, 81x+10, 121x+15, 169x+21,.... . Given x is equal to Tn, these formulas yield T3n+1, T5n+2, T7n+3, T9n+4, and so on.
The sum of the reciprocalsMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of all the triangular numbers is:
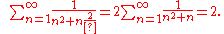
This can be shown by using the basic sum of a telescoping series:

Two other interesting formulas regarding triangular numbers are:

and

both of which can easily be established either by looking at dot patterns (see above) or with some simple algebra.
In 1796, German mathematician and scientist Carl Friedrich GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
discovered that every positive integer is representable as a sum of at most three triangular numbers, writing in his diary his famous words, "EΥΡHKA!Eureka (word)"Eureka" is an interjection used to celebrate a discovery, a transliteration of a word attributed to Archimedes.-Etymology:The word comes from ancient Greek εὕρηκα heúrēka "I have found ", which is the 1st person singular perfect indicative active of the verb heuriskō "I find"...
num = Δ + Δ + Δ" Note that this theorem does not imply that the triangular numbers are different (as in the case of 20=10+10), nor that a solution with three nonzero triangular numbers must exist. This is a special case of Fermat's Polygonal Number TheoremFermat polygonal number theoremIn additive number theory, the Fermat polygonal number theorem states that every positive integer is a sum of at most -gonal numbers. That is, every positive number can be written as the sum of three or fewer triangular numbers, and as the sum of four or fewer square numbers, and as the sum of...
.
The largest triangular number of the form 2k-1 is 4095, see Ramanujan–Nagell equation.
Wacław Franciszek Sierpiński posed the question as to the existence of four distinct triangular numbers in geometric progressionGeometric progressionIn mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. It was conjectured by Polish mathematician Kazimierz Szymiczek to be impossible. This conjecture was proven by Fang and Chen in 2007.
Triangular roots and tests for triangular numbers
By analogy with the square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of , one can define the (positive) triangular root of as the number n such that :

An integer is triangular if and only if is a square. Equivalently, if the positive triangular root of is an integer, then is the th triangular number.
See also
- 1 + 2 + 3 + 4 + …
- Metcalfe's lawMetcalfe's lawMetcalfe's law states that the value of a telecommunications network is proportional to the square of the number of connected usersof the system...
, that the complexity of communication between a group of people grows with the number of pairs of people, a triangular number. - Miraculous Draught of Fish, an episode from the GospelGospelA gospel is an account, often written, that describes the life of Jesus of Nazareth. In a more general sense the term "gospel" may refer to the good news message of the New Testament. It is primarily used in reference to the four canonical gospels of Matthew, Mark, Luke, and John...
s involving the triangular number 153153 (number)One hundred fifty-three is the natural number following one hundred fifty-two and preceding one hundred fifty-four.-Mathematical properties:...
; the triangular form of this number was thought by Saint Augustine to be important in interpreting this passage. - Pentagonal numberPentagonal numberA pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
- Hexagonal numberHexagonal numberA hexagonal number is a figurate number. The nth hexagonal number will be the number of points in a hexagon with n regularly spaced points on a side.The formula for the nth hexagonal number...
External links
- Triangular numbers at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- There exist triangular numbers that are also square at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Triangular numbers via 12 days of Christmas by Vi HartVi HartVi Hart is a "full-time recreational mathemusician", a creator of mathematical videos on YouTube.She is the daughter of mathematical sculptor George W. Hart and his former wife Carol Hart, and has collaborated with MIT computer science professor Erik Demaine.-External links:**...
- where Mp is a Mersenne prime

