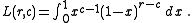Leibniz harmonic triangle
Encyclopedia
The Leibniz harmonic triangle is a triangular
arrangement of fractions
in which the outermost diagonals consist of the reciprocal
s of the row numbers and each inner cell is the absolute value
of the cell above minus the cell to the left. To put it algebra
ically, (where is the number of the row, starting from 1, and is the column number, never more than r) and
The first eight rows are:
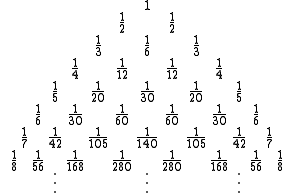
The denominators are listed in , while the numerators are all 1s.
Whereas each entry in Pascal's triangle
is the sum of the two entries in the above row, each entry in the Leibniz triangle is the sum of the two entries in the row below it. For example, in the 5th row, the entry (1/30) is the sum of the two (1/60)s in the 6th row.
Just as Pascal's triangle can be computed by using binomial coefficients, so can Leibniz's: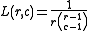 . Furthermore, the entries of this triangle can be computed from Pascal's, "the terms in each row are the initial term divided by the corresponding Pascal triangle entries."
. Furthermore, the entries of this triangle can be computed from Pascal's, "the terms in each row are the initial term divided by the corresponding Pascal triangle entries."
This triangle can be used to obtain examples for the Erdős–Straus conjecture
when n is divisible by 4.
If one takes the denominators of the nth row and adds them, then the result will equal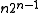 . For example, for the 3rd row, we have 3 + 6 + 3 = 12 = 3 × 22.
. For example, for the 3rd row, we have 3 + 6 + 3 = 12 = 3 × 22.
It is worth noting that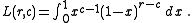
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
arrangement of fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
in which the outermost diagonals consist of the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s of the row numbers and each inner cell is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the cell above minus the cell to the left. To put it algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ically, (where is the number of the row, starting from 1, and is the column number, never more than r) and
The first eight rows are:

The denominators are listed in , while the numerators are all 1s.
Whereas each entry in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
is the sum of the two entries in the above row, each entry in the Leibniz triangle is the sum of the two entries in the row below it. For example, in the 5th row, the entry (1/30) is the sum of the two (1/60)s in the 6th row.
Just as Pascal's triangle can be computed by using binomial coefficients, so can Leibniz's:
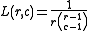 . Furthermore, the entries of this triangle can be computed from Pascal's, "the terms in each row are the initial term divided by the corresponding Pascal triangle entries."
. Furthermore, the entries of this triangle can be computed from Pascal's, "the terms in each row are the initial term divided by the corresponding Pascal triangle entries."This triangle can be used to obtain examples for the Erdős–Straus conjecture
Erdos–Straus conjecture
In number theory, the Erdős–Straus conjecture states that for all integers n ≥ 2, the rational number 4/n can be expressed as the sum of three unit fractions. Paul Erdős and Ernst G...
when n is divisible by 4.
If one takes the denominators of the nth row and adds them, then the result will equal
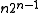 . For example, for the 3rd row, we have 3 + 6 + 3 = 12 = 3 × 22.
. For example, for the 3rd row, we have 3 + 6 + 3 = 12 = 3 × 22.It is worth noting that