
Rule 90
Encyclopedia

Elementary cellular automaton
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors....
based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value; in each time step all values are simultaneously replaced by the exclusive or of the two neighboring values. call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram
Stephen Wolfram
Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
's 2002 book A New Kind of Science
A New Kind of Science
A New Kind of Science is a book by Stephen Wolfram, published in 2002. It contains an empirical and systematic study of computational systems such as cellular automata...
. When started from a random initial configuration, its configuration remains random at each time step; however, any configuration with only finitely many nonzero cells becomes a replicator that eventually fills all of the cells with copies of itself.
Rules
An elementary cellular automatonElementary cellular automaton
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors....
consists of a one-dimensional array of cells, each of which holds a single binary value, either 0 or 1. An assignment of values to all of the cells is called a configuration. The automaton is given an initial configuration, after which its configuration repeatedly changes in a sequence of discrete time steps. At each step, all cells are updated simultaneously, according to a pre-specified rule which determines the new value as a function of each cell's previous value and of the values in its two neighboring cells. All cells obey the same rule, which may be given either as a formula or as a rule table that specifies the new value for each possible combination of neighboring values.
In the case of Rule 90, each cell's new value is the exclusive or of the two neighboring values. Equivalently, the next state of this particular automaton is governed by the following rule table:
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| new state for center cell | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Naming
The name of Rule 90 comes from Stephen WolframStephen Wolfram
Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
's binary-decimal notation
Wolfram code
Wolfram code is a naming system often used for one-dimensional cellular automaton rules, introduced by Stephen Wolfram in a 1983 paper and used in his book A New Kind of Science....
for one-dimensional cellular automaton rules. To calculate the notation for the rule, concatenate the new states in the rule table into a single binary number, and convert the number into decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
: 010110102 = 9010. Rule 90 has also been called the Sierpiński automaton, due to the characteristic Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
shape it generates, and the Martin–Odlyzko–Wolfram cellular automaton after the early research of on this automaton.
Additivity, superposition, and decomposition
A configuration in Rule 90 can be partitioned into two subsets of cells that do not interact with each other. One of these two subsets consists of the cells in even positions at even time steps and the cells in odd positions in odd time steps; the other subset consists of the cells in even positions at odd time steps and the cells in odd positions at even time steps. Each of these two subsets can be viewed as emulating a cellular automaton with only its half of the cells.Rule 90 is an additive cellular automaton: if two initial states are combined by computing the exclusive or of each their states, then their subsequent configurations will be combined in the same way. Thus, more generally, one can partition any configuration into two subsets with disjoint nonzero cells, evolve the two subsets separately, and compute the behavior of the original automaton by superposing configurations derived from the two subsets.
Stunted trees and triangular clearings
The Rule 90 automaton (in its equivalent form on one of the two independent subsets of alternating cells) was investigated in the early 1970s, in an attempt to gain additional insight into Gilbreath's conjectureGilbreath's conjecture
Gilbreath's conjecture is a hypothesis, or a conjecture, in number theory regarding the sequences generated by applying the forward difference operator to consecutive prime numbers and leaving the results unsigned, and then repeating this process on consecutive terms in the resulting sequence, and...
on the differences of consecutive prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s: in the triangle of numbers generated from the primes by repeatedly applying the forward difference operator, most values are either 0 or 2, and Rule 90 describes the pattern of nonzeros that arises once all other values have been eliminated. explained the rule by a metaphor of tree growth in a forest: each time step represents a height above the ground (with the initial configuration representing the ground level) and each nonzero cell represents a growing tree branch. At each successive level, a branch can grow into one of the cells only when there is no other branch competing for the same cell.
From any initial configuration of Rule 90, one may form a mathematical forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
in which every node has at most one outgoing edge, by creating a node for each pair such that cell is nonzero at time , and by connecting each such node (with ) to the unique nonzero neighbor of in time step . Miller observed that these forests develop triangular "clearings", regions of the time-space diagram with no nonzero cells bounded by a flat bottom edge and diagonal sides. For random initial conditions, the boundaries between the trees formed in this way themselves shift in a seemingly random pattern, and trees frequently die out altogether. But by means of the theory of shift register
Shift register
In digital circuits, a shift register is a cascade of flip flops, sharing the same clock, which has the output of any one but the last flip-flop connected to the "data" input of the next one in the chain, resulting in a circuit that shifts by one position the one-dimensional "bit array" stored in...
s he and others were able to find initial conditions in which the trees all remain alive forever, the pattern of growth repeats periodically, and all of the clearings can be guaranteed to remain bounded in size.
Additionally, Miller used these regular patterns to form the designs of tapestries
Tapestry
Tapestry is a form of textile art, traditionally woven on a vertical loom, however it can also be woven on a floor loom as well. It is composed of two sets of interlaced threads, those running parallel to the length and those parallel to the width ; the warp threads are set up under tension on a...
depicting physical trees as well as abstract patterns of triangles.
Sierpiński triangle
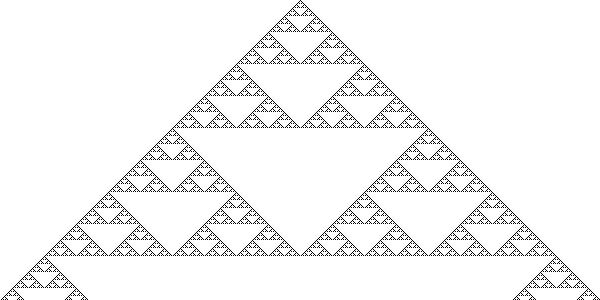
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
when responding to an initial state with a single nonzero cell. Rules 18, 22, 26, 82, 146, 154, 210 and 218 generate the same sequence. In Rule 90, each cell is the exclusive or of its two neighbors. Because this is equivalent to modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
-2 addition, this generates the modulo-2 version of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, which is a discrete version of the Sierpiński triangle.
The number of live cells in the th row of this pattern is , where is the number of nonzero digits in the binary representation of the number . The sequence of these numbers of live cells,
- 1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, 4, 8, 4, 8, 8, 16, 4, 8, 8, 16, 8, 16, 16, 32, ...
known as Gould's sequence or Dress's sequence, has a characteristic exponentially growing sawtooth
Sawtooth wave
The sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
shape that can be used to recognize physical processes that behave similarly to Rule 90.
The Sierpiński triangle also occurs in a more subtle way in the evolution of any configuration in Rule 90. At any time step in the Rule's evolution, each cell has a state that is the exclusive or of a subset of the cells in the initial configuration; that subset has the same shape as the th row of the Sierpiński triangle.
Replication
In the Sierpiński triangle, for any integer , the rows with positions that are multiples of consist of some number of nonzero cells spaced units apart. Therefore, because of the additive property of Rule 90, if an initial configuration consists of a finite pattern of nonzero cells with width less than , then in steps that are multiples of , the configuration will consist of copies of spaced units from start to start; this spacing is wide enough to prevent the copies from interfering with each other. The number of copies is the same as the number of nonzero cells in the corresponding row of the Sierpiński triangle. Thus, in this rule, every pattern is a replicator: it generates multiple copies of itself that spread out across the configuration, eventually filling the whole array. However, unlike the replicators in more complex rules such as the Von Neumann universal constructorVon Neumann universal constructor
John von Neumann's Universal Constructor is a self-replicating machine in a cellular automata environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in...
, Codd's cellular automaton
Codd's cellular automaton
Codd's cellular automaton is a cellular automaton devised by the British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29...
, or Langton's loops
Langton's loops
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm" , which will become the daughter loop...
, the replication in Rule 90 is trivial and automatic, rather than requiring each replicator pattern to carry and copy a sequence of instructions for building itself.
Predecessors and Gardens of Eden
In Rule 90, on an infinite one-dimensional lattice, every configuration has exactly four predecessor configurations: in the predecessor, any two consecutive cells may have any combination of states, but once those two cells' states are chosen, there is only one consistent choice for the states of the remaining cells. Therefore, this rule provides an example of a cellular automaton that is surjectiveSurjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
(each configuration has a predecessor, so there is no Garden of Eden) but not injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
(unlike injective rules, Rule 90 has pairs of configurations with the same successor). The Garden of Eden theorem of Moore and Myhill implies that every injective cellular automaton must be surjective, but this example shows that the converse is not true.
Because each state has a bounded number of predecessors, the evolution of Rule 90 preserves the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of any configuration. In particular, if an infinite initial configuration is selected by choosing the state of each cell independently at random, with each of the two states being equally likely to be selected, then each subsequent configuration can be described by exactly the same probability distribution.
The Rule 90 configuration consisting of a single nonzero cell (with all other cells zero) has no predecessor that have finitely many nonzeros, but it is not a Garden of Eden because it has predecessors with infinitely many nonzeros.
Emulation by other systems

Tag system
A tag system is a deterministic computational model published by Emil Leon Post in 1943 as a simple form of Post canonical system. A tag system may also be viewed as an abstract machine, called a Post tag machine —briefly, a finite state machine whose only tape is a FIFO queue of unbounded length,...
s, and in two-dimensional cellular automata including Wireworld. Rule 90 can also simulate itself in the same way: if each cell of a Rule 90 configuration is replaced by a pair of consecutive cells, in which the first cell in the pair contains the original cell's value, and the second contains a zero, then this doubled configuration has the same behavior as the original configuration at half the speed.
Various other cellular automata are known to support replicators, patterns that make copies of themselves, with the same behavior as in the tree growth model for Rule 90: a new copy is placed to either side of the replicator pattern, as long as the space there is empty, but if two replicators both attempt to copy themselves into the same position, then the space remains blank, and in either case the replicators themselves vanish, leaving their copies to carry on the replication. A standard example of this behavior is the "bowtie pasta" pattern in the two-dimensional HighLife
HighLife
HighLife is a cellular automaton similar to Conway's Game of Life. It was devised in 1994 by Nathan Thompson. It is a two-dimensional, two-state cellular automaton in the "Life family" and is described by the rule B36/S23; that is, a cell is born if it has 3 or 6 neighbors and survives if it has 2...
rule, a rule that except for the behavior of this pattern behaves in many ways like Conway's Game of Life. Whenever a pattern supports replicators with this growth pattern, one-dimensional arrays of replicators can be used to simulate Rule 90. Rule 90 (on finite rows of cells) can also be simulated by the block oscillators of the two-dimensional Life-like cellular automaton
Life-like cellular automaton
A cellular automaton is Life-like if it meets the following criteria:* The array of cells of the automaton has two dimensions....
B36/S125, also called "2x2", and the behavior of Rule 90 can be used to characterize the possible periods of these oscillators.

