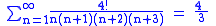
Pentatope number
Encyclopedia
A pentatope number is a number in the fifth cell of any row of Pascal's triangle
starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.
The first few numbers of this kind are :
Pentatope numbers belong in the class of figurate number
s, which can be represented as regular, discrete geometric patterns. The formula for the nth pentatopic number is:
Two of every three pentatope numbers are also pentagonal number
s. To be precise, the (3k − 2)th pentatope number is always the ((3k2 − k)/2)th pentagonal number and the (3k − 1)th pentatope number is always the ((3k2 + k)/2)th pentagonal number. The 3kth pentatope number is the generalized pentagonal number
obtained by taking the negative index −(3k2 + k)/2 in the formula for pentagonal numbers. (These expressions always give integers).
The infinite sum of the reciprocals of all pentatopal numbers is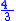
. This can be derived using telescoping series.
Pentatopal numbers can also be represented as the sum of the first n tetrahedral number
s.
If the corners of a polygon of size n are all connected to one another, the number of intersections created will be a pentatope number. For example, a triangle has 0 intersections, a square has 1, a pentagon has 5, a hexagon has 15, and a heptagon has 35.
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.
The first few numbers of this kind are :
- 1, 5, 1515 (number)15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 3535 (number)35 is the natural number following 34 and preceding 36.- In mathematics :35 is the sum of the first five triangular numbers, making it a tetrahedral number....
, 7070 (number)70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the...
, 126126 (number)126 is the natural number following 125 and preceding 127.-In mathematics:One hundred [and] twenty-six is a pentagonal pyramidal number, and a decagonal number as well as a pentatope number....
, 210, 330, 495495 (number)495 is the integer after 494 and before 496. It is a pentatope number.- Kaprekar transformation :The Kaprekar transformation is defined as follows for three-digit numbers:# Start with a three-digit number with at least two digits different....
, 715, 10011001 (number)1001 is the natural number following 1000 and followed by 1002.- In mathematics :One thousand and one is a sphenic number, a pentagonal number, a pentatope number and the first four-digit palindromic number.- In other fields :...
, 1365
Figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...
s, which can be represented as regular, discrete geometric patterns. The formula for the nth pentatopic number is:
Two of every three pentatope numbers are also pentagonal number
Pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
s. To be precise, the (3k − 2)th pentatope number is always the ((3k2 − k)/2)th pentagonal number and the (3k − 1)th pentatope number is always the ((3k2 + k)/2)th pentagonal number. The 3kth pentatope number is the generalized pentagonal number
Pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
obtained by taking the negative index −(3k2 + k)/2 in the formula for pentagonal numbers. (These expressions always give integers).
The infinite sum of the reciprocals of all pentatopal numbers is
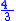. This can be derived using telescoping series.
Pentatopal numbers can also be represented as the sum of the first n tetrahedral number
Tetrahedral number
A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
s.
If the corners of a polygon of size n are all connected to one another, the number of intersections created will be a pentatope number. For example, a triangle has 0 intersections, a square has 1, a pentagon has 5, a hexagon has 15, and a heptagon has 35.