
Newton's theorem of revolving orbits
Encyclopedia
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
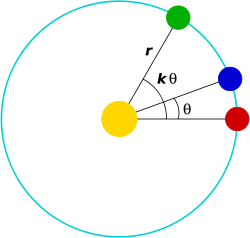
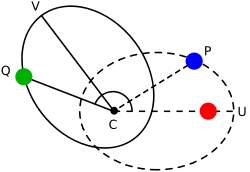
, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s. The term "radial motion" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.
Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.
As noted by astrophysicist Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar, FRS ) was an Indian origin American astrophysicist who, with William A. Fowler, won the 1983 Nobel Prize for Physics for key discoveries that led to the currently accepted theory on the later evolutionary stages of massive stars...
in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell
Donald Lynden-Bell
Donald Lynden-Bell CBE FRS is an English astrophysicist, best known for his theories that galaxies contain massive black holes at their centre, and that such black holes are the principal source of energy in quasars. He was a co-recipient, with Maarten Schmidt, of the inaugural Kavli Prize for...
and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.
Historical context

The motion of astronomical bodies has been studied systematically for thousands of years. The stars were observed to rotate uniformly, always maintaining the same relative positions to one another. However, other bodies were observed to wander against the background of the fixed stars; most such bodies were called planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s after the Greek word "πλανήτοι" (planētoi) for "wanderers". Although they generally move in the same direction along a path across the sky (the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
), individual planets sometimes reverse their direction briefly, exhibiting retrograde motion
Retrograde motion
Retrograde motion is motion in the direction opposite to the movement of something else, and is the contrary of direct or prograde motion. This motion can be the orbit of one body about another body or about some other point, or the rotation of a single body about its axis, or other phenomena such...
.
To describe this forward-and-backward motion, Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
developed the concept of deferents and epicycles
Deferent and epicycle
In the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
, according to which the planets are carried on rotating circles that are themselves carried on other rotating circles, and so on. Any orbit can be described with a sufficient number of judiciously chosen epicycles, since this approach corresponds to a modern Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. Roughly 350 years later, Claudius Ptolemaeus
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
published his Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
, in which he developed this system to match the best astronomical observations of his era. To explain the epicycles, Ptolemy adopted the geocentric
Geocentric model
In astronomy, the geocentric model , is the superseded theory that the Earth is the center of the universe, and that all other objects orbit around it. This geocentric model served as the predominant cosmological system in many ancient civilizations such as ancient Greece...
cosmology of Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
, according to which planets were confined to concentric rotating spheres. This model of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
was authoritative for nearly 1500 years.
The modern understanding of planetary motion arose from the combined efforts of astronomer Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
and physicist Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
in the 16th century. Tycho is credited with extremely accurate measurements of planetary motions, from which Kepler was able to derive his laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. According to these laws, planets move on ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s (not epicycles) about the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
(not the Earth). Kepler's second and third laws make specific quantitative predictions: planets sweep out equal areas in equal time, and the square of their orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
s equals a fixed constant times the cube of their semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
. Subsequent observations of the planetary orbits showed that the long axis of the ellipse (the so-called line of apsides) rotates gradually with time; this rotation is known as apsidal precession. The apses
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
of an orbit are the points at which the orbiting body is closest or furthest away from the attracting center; for planets orbiting the Sun, the apses correspond to the perihelion (closest) and aphelion (furthest).
With the publication of his Principia roughly eighty years later (1687), Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
provided a physical theory that accounted for all three of Kepler's laws, a theory based on Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and his law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
. In particular, Newton proposed that the gravitational force between any two bodies was a central force F(r) that varied as the inverse square
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
of the distance r between them. Arguing from his laws of motion, Newton showed that the orbit of any particle acted upon by one such force is always a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, specifically an ellipse if it does not go to infinity. However, this conclusion holds only when two bodies are present (the two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
); the motion of three bodies or more acting under their mutual gravitation (the n-body problem
N-body problem
The n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
) remained unsolved for centuries after Newton, although solutions to a few special cases
Euler's three-body problem
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
were discovered. Newton proposed that the orbits of planets about the Sun are largely elliptical because the Sun's gravitation is dominant; to first approximation
Orders of approximation
In science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
, the presence of the other planets can be ignored. By analogy, the elliptical orbit of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
about the Earth was dominated by the Earth's gravity; to first approximation, the Sun's gravity and those of other bodies of the Solar System can be neglected. However, Newton stated that the gradual apsidal precession of the planetary and lunar orbits was due to the effects of these neglected interactions; in particular, he stated that the precession of the Moon's orbit was due to the perturbing effects of gravitational interactions with the Sun.
Newton's theorem of revolving orbits was his first attempt to understand apsidal precession quantitatively. According to this theorem, the addition of a particular type of central force—the inverse-cube force—can produce a rotating orbit; the angular speed is multiplied by a factor k, whereas the radial motion is left unchanged. However, this theorem is restricted to a specific type of force that may not be relevant; several perturbing inverse-square interactions (such as those of other planets) seem unlikely to sum exactly to an inverse-cube force. To make his theorem applicable to other types of forces, Newton found the best approximation of an arbitrary central force F(r) to an inverse-cube potential in the limit of nearly circular orbits, that is, elliptical orbits of low eccentricity, as is indeed true for most orbits in the Solar System. To find this approximation, Newton developed an infinite series that can be viewed as the forerunner of the Taylor expansion. This approximation allowed Newton to estimate the rate of precession for arbitrary central forces. Newton applied this approximation to test models of the force causing the apsidal precession of the Moon's orbit. However, the problem of the Moon's motion is dauntingly complex, and Newton never published an accurate gravitational model of the Moon's apsidal precession. After a more accurate model by Clairaut in 1747, analytical models of the Moon's motion were developed in the late 19th century by Hill
George William Hill
George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
, Brown, and Delaunay
Charles-Eugène Delaunay
Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
.
However, Newton's theorem is more general than merely explaining apsidal precession. It describes the effects of adding an inverse-cube force to any central force F(r), not only to inverse-square forces such as Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
and Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. Newton's theorem simplifies orbital problems in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
by eliminating inverse-cube forces from consideration. The radial and angular motions, r(t) and θ1(t), can be calculated without the inverse-cube force; afterwards, its effect can be calculated by multiplying the angular speed of the particle
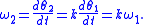
Mathematical statement
Consider a particle moving under an arbitrary central force F1(r) whose magnitude depends only on the distance r between the particle and a fixed center. Since the motion of a particle under a central force always lies in a plane, the position of the particle can be described by polar coordinatesPolar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
(r, θ1), the radius and angle of the particle relative to the center of force (Figure 1). Both of these coordinates, r(t) and θ1(t), change with time t as the particle moves.
Imagine a second particle with the same mass m and with the same radial motion r(t), but one whose angular speed is k times faster than that of the first particle, where k is any constant. In other words, the azimuthal angles of the two particles are related by the equation θ2(t) = k θ1(t). Newton showed that the motion of the second particle can be produced by adding an inverse-cube central force to whatever force F1(r) acts on the first particle

where L1 is the magnitude of the first particle's angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, which is a constant of motion
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
(conserved) for central forces.
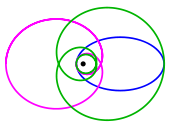
If k2 is greater than one, F2 − F1 is a negative number; thus, the added inverse-cube force is attractive, as observed in the green planet of Figures 1–4 and 9. By contrast, if k2 is less than one, F2−F1 is a positive number; the added inverse-cube force is repulsive, as observed in the green planet of Figures 5 and 10, and in the red planet of Figures 4 and 5.
Alteration of the particle path
The addition of such an inverse-cube force also changes the path followed by the particle. The path of the particle ignores the time dependencies of the radial and angular motions, such as r(t) and θ1(t); rather, it relates the radius and angle variables to one another. For this purpose, the angle variable is unrestricted and can increase indefinitely as the particle revolves around the central point multiple times. For example, if the particle revolves twice about the central point and returns to its starting position, its final angle is not the same as its initial angle; rather, it has increased by . Formally, the angle variable is defined as the integral of the angular speed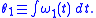
A similar definition holds for θ2, the angle of the second particle.
If the path of the first particle is described in the form , the path of the second particle is given by the function , since . For example, let the path of the first particle be an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
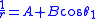
where A and B are constants; then, the path of the second particle is given by
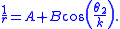
Orbital precession
If k is close, but not equal, to one, the second orbit resembles the first, but revolves gradually about the center of force; this is known as orbital precession (Figure 3). If k is greater than one, the orbit precesses in the same direction as the orbit (Figure 3); if k is less than one, the orbit precesses in the opposite direction.Although the orbit in Figure 3 may seem to rotate uniformly, i.e., at a constant angular speed, this is true only for circular orbits. If the orbit rotates at an angular speed Ω, the angular speed of the second particle is faster or slower than that of the first particle by Ω; in other words, the angular speeds would satisfy the equation . However, Newton's theorem of revolving orbits states that the angular speeds are related by multiplication: , where k is a constant. Combining these two equations shows that the angular speed of the precession equals . Hence, Ω is constant only if ω1 is constant. According to the conservation of angular momentum, ω1 changes with the radius r

where m and L1 are the first particle's mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, respectively, both of which are constant. Hence, ω1 is constant only if the radius r is constant, i.e., when the orbit is a circle. However, in that case, the orbit does not change as it precesses.
Illustrative example: Cotes' spirals
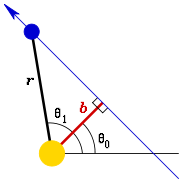
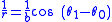
where θ0 is the angle at which the distance is minimized (Figure 6). The distance r begins at infinity (when θ1 – ), and decreases gradually until θ1 – , when the distance reaches a minimum, then gradually increases again to infinity at θ1 – . The minimum distance b is the impact parameter
Impact parameter
The impact parameter b is defined as the perpendicular distance between the path of a projectile and the center of the field U created by an object that the projectile is approaching...
, which is defined as the length of the perpendicular from the fixed center to the line of motion. The same radial motion is possible when an inverse-cube central force is added.

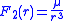
where the numerator μ may be positive (repulsive) or negative (attractive). If such an inverse-cube force is introduced, Newton's theorem says that the corresponding solutions have a shape called Cotes' spirals. These are curves defined by the equation
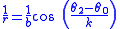
where the constant k equals
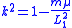
When the right-hand side of the equation is a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, the solution corresponds to an epispiral. When the argument θ1 – θ0 equals ±90°×k, the cosine goes to zero and the radius goes to infinity. Thus, when k is less than one, the range of allowed angles becomes small and the force is repulsive (red curve on right in Figure 7). On the other hand, when k is greater than one, the range of allowed angles increases, corresponding to an attractive force (green, cyan and blue curves on left in Figure 7); the orbit of the particle can even wrap around the center several times. The possible values of the parameter k may range from zero to infinity, which corresponds to values of μ ranging from negative infinity up to the positive upper limit, L12/m. Thus, for all attractive inverse-cube forces (negative μ) there is a corresponding epispiral orbit, as for some repulsive ones (μ < L12/m), as illustrated in Figure 7. Stronger repulsive forces correspond to a faster linear motion.


where the constant λ satifies

This form of Cotes' spirals corresponds to one of the two Poinsot's spirals (Figure 8). The possible values of λ range from zero to infinity, which corresponds to values of μ greater than the positive number L12/m. Thus, Poinsot spiral motion only occurs for repulsive inverse-cube central forces, and applies in the case that L is not too large for the given μ.
Taking the limit of k or λ going to zero yields the third form of a Cotes' spiral, the so-called reciprocal spiral or hyperbolic spiral
Hyperbolic spiral
thumb|200px|right|Hyperbolic spiral for a=2A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral. A hyperbolic spiral is the opposite of an Archimedean spiral and are a type of Cotes' spiral.It has the polar equation:...
, as a solution

where A and ε are arbitrary constants. Such curves result when the strength μ of the repulsive force exactly balances the angular momentum-mass term
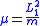
Closed orbits and inverse-cube central forces
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
, and inverse-square forces, , such as Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
and Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
—have a very unusual property. A particle moving under either type of force always returns to its starting place with its initial velocity, provided that it lacks sufficient energy to move out to infinity. In other words, the path of a bound particle is always closed and its motion repeats indefinitely, no matter what its initial position or velocity. As shown by Bertrand's theorem, this property is not true for other types of forces; in general, a particle will not return to its starting point with the same velocity.
However, Newton's theorem shows that an inverse-cubic force may be applied to a particle moving under a linear or inverse-square force such that its orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
remains closed, provided that k equals a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. (A number is called "rational" if it can be written as a fraction m/n, where m and n are integers.) In such cases, the addition of the inverse-cubic force causes the particle to complete m rotations about the center of force in the same time that the original particle completes n rotations. This method for producing closed orbits does not violate Bertrand's theorem, because the added inverse-cubic force depends on the initial velocity of the particle.

Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of an integer, i.e., if in the formula . For example, if (green planet in Figure 5, green orbit in Figure 10), the resulting orbit is called the third subharmonic of the original orbit. Although such orbits are unlikely to occur in nature, they are helpful for illustrating Newton's theorem.
Limit of nearly circular orbits
In Proposition 45 of his Principia, Newton applies his theorem of revolving orbits to develop a method for finding the force laws that govern the motions of planets. Johannes KeplerJohannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
had noted that the orbits of most planets and the Moon seemed to be ellipses, and the long axis of those ellipses can determined accurately from astronomical measurements. The long axis is defined as the line connecting the positions of minimum and maximum distances to the central point, i.e., the line connecting the two apses
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
. For illustration, the long axis of the planet Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
is defined as the line through its successive positions of perihelion and aphelion. Over time, the long axis of most orbiting bodies rotates gradually, generally no more than a few degrees per complete revolution, because of gravitational perturbations from other bodies, oblateness in the attracting body, general relativistic effects, and other effects. Newton's method uses this apsidal precession as a sensitive probe of the type of force being applied to the planets.
Newton's theorem describes only the effects of adding an inverse-cube central force. However, Newton extends his theorem to an arbitrary central forces F(r) by restricting his attention to orbits that are nearly circular, such as ellipses with low orbital eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
(ε ≤ 10%), which is true of seven of the eight planetary orbits in the solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
. Newton also applied his theorem to the planet Mercury, which has an eccentricity ε of roughly 21%, and suggested that it may pertain to Halley's comet, whose orbit has an eccentricity of roughly 97%.
A qualitative justification for this extrapolation of his method has been suggested by Valluri, Wilson and Harper. According to their argument, Newton considered the apsidal precession angle α (the angle between the vectors of successive minimum and maximum distance from the center) to be a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of the orbital eccentricity ε. For the inverse-square force, α equals 180°; the vectors to the positions of minimum and maximum distances lie on the same line. If α is initially not 180° at low ε (quasi-circular orbits) then, in general, α will equal 180° only for isolated values of ε; a randomly chosen value of ε would be very unlikely to give α = 180°. Therefore, the observed slow rotation of the apsides of planetary orbits suggest that the force of gravity is an inverse-square law.
Quantitative formula
To simplify the equations, Newton writes F(r) in terms of a new function C(r)
where R is the average radius of the nearly circular orbit. Newton expands C(r) in a series—now known as a Taylor expansion—in powers of the distance r, one of the first appearances of such a series. By equating the resulting inverse-cube force term with the inverse-cube force for revolving orbits, Newton derives an equivalent angular scaling factor k for nearly circular orbits

In other words, the application of an arbitrary central force F(r) to a nearly circular elliptical orbit can accelerate the angular motion by the factor k without affecting the radial motion significantly. If an elliptical orbit is stationary, the particle rotates about the center of force by 180° as it moves from one end of the long axis to the other (the two apse
Apse
In architecture, the apse is a semicircular recess covered with a hemispherical vault or semi-dome...
s). Thus, the corresponding apsidal angle α for a general central force equals k×180°, using the general law .
Examples
Newton illustrates his formula with three examples. In the first two, the central force is a power lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
, and, hence,C(r) is proportional to rn. The formula above indicates that the angular motion is multiplied by a factor , so that the apsidal angle α equals 180°/√n.
This angular scaling can be seen in the apsidal precession, i.e., in the gradual rotation of the long axis of the ellipse (Figure 3). As noted above, the orbit as a whole rotates with a mean angular speed Ω=(k−1)ω, where ω equals the mean angular speed of the particle about the stationary ellipse. If the particle requires a time T to move from one apse to the other, this implies that, in the same time, the long axis will rotate by an angle β = ΩT = (k − 1)ωT = (k − 1)×180°. For an inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
such as Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, where n equals 1, there is no angular scaling (k = 1), the apsidal angle α is 180°, and the elliptical orbit is stationary (Ω = β = 0).
As a final illustration, Newton considers a sum of two power laws
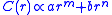
which multiplies the angular speed by a factor

Newton applies both of these formulae (the power law and sum of two power laws) to examine the apsidal precession of the Moon's orbit.
Precession of the Moon's orbit

Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
can be measured accurately, and is noticeably more complex than that, of the planets. The ancient Greek astronomers, Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
and Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
, had noted several periodic variations in the Moon's orbit, such as small oscillations in its orbital eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
and the inclination
Inclination
Inclination in general is the angle between a reference plane and another plane or axis of direction.-Orbits:The inclination is one of the six orbital parameters describing the shape and orientation of a celestial orbit...
of its orbit to the plane of the ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
. These oscillations generally occur on a once-monthly or twice-monthly time-scale. The line of its apses
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
precesses gradually with a period of roughly 8.85 years, while its line of nodes
Longitude of the ascending node
The longitude of the ascending node is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a reference direction, called the origin of longitude, to the direction of the ascending node, measured in a reference plane...
turns a full circle in roughly double that time, 18.6 years. This accounts for the roughly 18-year periodicity of eclipse
Eclipse
An eclipse is an astronomical event that occurs when an astronomical object is temporarily obscured, either by passing into the shadow of another body or by having another body pass between it and the viewer...
s, the so-called Saros cycle
Saros cycle
The saros is a period of 223 synodic months , that can be used to predict eclipses of the Sun and Moon. One saros after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle...
. However, both lines experience small fluctuations in their motion, again on the monthly time-scale.
In 1673, Jeremiah Horrocks
Jeremiah Horrocks
Jeremiah Horrocks , sometimes given as Jeremiah Horrox , was an English astronomer who was the only person to predict, and one of only two people to observe and record, the transit of Venus of 1639.- Life and work :Horrocks was born in Lower Lodge, in...
published a reasonably accurate model of the Moon's motion in which the Moon was assumed to follow a precessing elliptical orbit. An sufficiently accurate and simple method for predicting the Moon's motion would have solved the navigational problem of determining a ship's longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
; in Newton's time, the goal was to predict the Moon's position to 2' (two arc-minutes
Minute of arc
A minute of arc, arcminute, or minute of angle , is a unit of angular measurement equal to one sixtieth of one degree. In turn, a second of arc or arcsecond is one sixtieth of one minute of arc....
), which would correspond to a 1° error in terrestrial longitude. Horrocks' model predicted the lunar position with errors no more than 10 arc-minutes; for comparison, the diameter of the Moon is roughly 30 arc-minutes.
Newton used his theorem of revolving orbits in two ways to account for the apsidal precession of the Moon. First, he showed that the Moon's observed apsidal precession could be accounted for by changing the force law of gravity
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
from an inverse-square law to a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
in which the exponent was (roughly 2.0165)
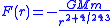
In 1894, Asaph Hall
Asaph Hall
Asaph Hall III was an American astronomer who is most famous for having discovered the moons of Mars in 1877...
adopted this approach of modifying the exponent in the inverse-square law slightly to explain an anomalous orbital precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, which had been observed in 1859 by Urbain Le Verrier. Ironically, Hall's theory was ruled out by careful astronomical observations of the Moon. The currently accepted explanation for this precession involves the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, which (to first approximation
Orders of approximation
In science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
) adds an inverse-quartic force, i.e., one that varies as the inverse fourth power of distance.
As a second approach to explaining the Moon's precession, Newton suggested that the perturbing influence of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
on the Moon's motion might be approximately equivalent to an additional linear force

The first term corresponds to the gravitational attraction between the Moon and the Earth, where r is the Moon's distance from the Earth. The second term, so Newton reasoned, might represent the average perturbing force of the Sun's gravity of the Earth-Moon system. Such a force law could also result if the Earth were surrounded by a spherical dust cloud of uniform density. Using the formula for k for nearly circular orbits, and estimates of A and B, Newton showed that this force law could not account for the Moon's precession, since the predicted apsidal angle α was (≈ 180.76°) rather than the observed α (≈ 181.525°). For every revolution, the long axis would rotate 1.5°, roughly half of the observed 3.0°
Generalization
Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
first published his theorem in 1687, as Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica. However, as astrophysicist Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar, FRS ) was an Indian origin American astrophysicist who, with William A. Fowler, won the 1983 Nobel Prize for Physics for key discoveries that led to the currently accepted theory on the later evolutionary stages of massive stars...
noted in his 1995 commentary on Newton's Principia, the theorem remained largely unknown and undeveloped for over three centuries.
The first generalization of Newton's theorem was discovered by Mahomed and Vawda in 2000. As Newton did, they assumed that the angular motion of the second particle was k times faster than that of the first particle, . In contrast to Newton, however, Mahomed and Vawda did not require that the radial motion of the two particles be the same, . Rather, they required that the inverse radii be related by a linear equation
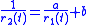
This transformation of the variables changes the path of the particle. If the path of the first particle is written , the second particle's path can be written as

If the motion of the first particle is produced by a central force F1(r), Mahomed and Vawda showed that the motion of the second particle can be produced by the following force
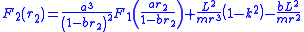
According to this equation, the second force F2(r) is obtained by scaling the first force and changing its argument, as well as by adding inverse-square and inverse-cube central forces.
For comparison, Newton's theorem of revolving orbits corresponds to the case and , so that . In this case, the original force is not scaled, and its argument is unchanged; the inverse-cube force is added, but the inverse-square term is not. Also, the path of the second particle is , consistent with the formula given above.
Newton's derivation
Newton's derivation is found in Section IX of his Principia, specifically Propositions 43–45. His derivations of these Propositions are based largely on geometry.Proposition 43; Problem 30
- It is required to make a body move in a curve that revolves about the center of force in the same manner as another body in the same curve at rest.
Newton's derivation of Proposition 43 depends on his Proposition 2, derived earlier in the Principia. Proposition 2 provides a geometrical test for whether the net force acting on a point mass (a particle) is a central force. Newton showed that a force is central if and only if the particle sweeps out equal areas in equal times as measured from the center.
Newton's derivation begins with a particle moving under an arbitrary central force F1(r); the motion of this particle under this force is described by its radius r(t) from the center as a function of time, and also its angle θ1(t). In an infinitesimal time dt, the particle sweeps out an approximate right triangle whose area is
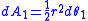
Since the force acting on the particle is assumed to be a central force, the particle sweeps out equal angles in equal times, by Newton's Proposition 2. Expressed another way, the rate of sweeping out area is constant
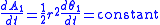
This constant areal velocity can be calculated as follows. At the apapsis and periapsis
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
, the positions of closest and furthest distance from the attracting center, the velocity and radius vectors are perpendicular; therefore, the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
L1 per mass m of the particle (written as h1) can be related to the rate of sweeping out areas

Now consider a second particle whose orbit is identical in its radius, but whose angular variation is multiplied by a constant factor k
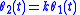
The areal velocity of the second particle equals that of the first particle multiplied by the same factor k

Since k is a constant, the second particle also sweeps out equal areas in equal times. Therefore, by Proposition 2, the second particle is also acted upon by a central force F2(r). This is the conclusion of Proposition 43.
Proposition 44
- The difference of the forces, by which two bodies may be made to move equally, one in a fixed, the other in the same orbit revolving, varies inversely as the cube of their common altitudes.
To find the magnitude of F2(r) from the original central force F1(r), Newton calculated their difference using geometry and the definition of centripetal acceleration. In Proposition 44 of his Principia, he showed that the difference is proportional to the inverse cube of the radius, specifically by the formula given above, which Newtons writes in terms of the two constant areal velocities, h1 and h2

Proposition 45; Problem 31
- To find the motion of the apsides in orbits approaching very near to circles.
In this Proposition, Newton derives the consequences of his theorem of revolving orbits in the limit of nearly circular orbits. This approximation is generally valid for planetary orbits and the orbit of the Moon about the Earth. This approximation also allows Newton to consider a great variety of central force laws, not merely inverse-square and inverse-cube force laws.
Modern derivation
Modern derivations of Newton's theorem have been published by WhittakerE. T. Whittaker
Edmund Taylor Whittaker FRS FRSE was an English mathematician who contributed widely to applied mathematics, mathematical physics and the theory of special functions. He had a particular interest in numerical analysis, but also worked on celestial mechanics and the history of physics...
(1937) and Chandrasekhar
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar, FRS ) was an Indian origin American astrophysicist who, with William A. Fowler, won the 1983 Nobel Prize for Physics for key discoveries that led to the currently accepted theory on the later evolutionary stages of massive stars...
(1995). By assumption, the second angular speed is k times faster than the first
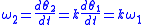
Since the two radii have the same behavior with time, r(t), the conserved angular momenta are related by the same factor k

The equation of motion for a radius r of a particle of mass m moving in a central potential V(r) is given by Lagrange's equations

Applying the general formula to the two orbits yields the equation

which can be re-arranged to the form

This equation relating the two radial forces can be understood qualitatively as follows. The difference in angular speeds (or equivalently, in angular momenta) causes a difference in the centripetal force
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
requirement; to offset this, the radial force must be altered with an inverse-cube force.
Newton's theorem can be expressed equivalently in terms of potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, which is defined for central forces
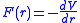
The radial force equation can be written in terms of the two potential energies
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

Integrating with respect to the distance r, Newtons's theorem states that a k-fold change in angular speed results from adding an inverse-square potential energy to any given potential energy V1(r)
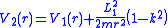
See also
- Kepler problemKepler problemIn classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
- Laplace–Runge–Lenz vector
- Bertrand's theorem
- Two-body problem in general relativity
- Newton's theorem about ovalsNewton's theorem about ovalsIn mathematics, Newton's theorem about ovals states that the area cut off by a secant of a smooth convex oval is not an algebraic function of the secant....
Further reading
(séance du lundi 20 Octobre 1873) Alternative translation of earlier (2nd) edition of Newton's Principia.External links
- Three-body problem discussed by Alain Chenciner at ScholarpediaScholarpediaScholarpedia is an English-language online wiki-based encyclopedia that uses the same MediaWiki software as Wikipedia, but has features more commonly associated with open-access online academic journals....

