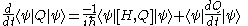Constant of motion
Encyclopedia
In mechanics
, a constant of motion is a quantity that is conserved
throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion
, rather than a physical constraint
(which would require extra constraint forces). Common examples include energy
, linear momentum, angular momentum and the Laplace–Runge–Lenz vector (for inverse-square force laws
).
. In fortunate cases, even the trajectory
of the motion can be derived as the intersection
of isosurface
s corresponding to the constants of motion. For example, Poinsot's construction shows that the torque-free rotation
of a rigid body
is the intersection of a sphere (conservation of total angular momentum) and an ellipsoid (conservation of energy), a trajectory that might be otherwise hard to derive and visualize. Therefore, the identification of constants of motion is an important objective in mechanics
.
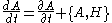
Another useful result is Poisson's theorem, which states that if two quantities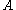
and 
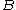are constants of motion, so is their Poisson bracket 
.
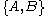A system with n degrees of freedom, and n constants of motion, such that the Poisson bracket of any pair of constants of motion vanishes, is known as a completely integrable system
. Such a collection of constants of motion are said to be in involution with each other.
with the hamiltonian
, H, and it does not itself depend explicitly on time. This is because
Where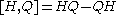
is the commutator relation.
And also, that there is a wave function which obeys Schrödinger's equation
Taking the time derivative of the expectation value of Q requires use of the product rule
, and results in
|
|
|-
|
|
|-
|
|
|-
|
|
|-
|
|
|}
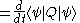
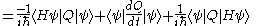
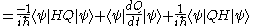
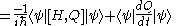
So finally,
|
|}
and Q is not explicitly dependent on time , then
But if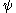
is an eigenstate of Hamiltonian, then even if
provided Q is not explicitly dependent on time.
|-
|
|}
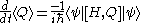
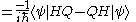
Since
This is the reason why Eigen states of Hamiltonian are also called as stationary states.
has constants of motion other than the energy. By contrast, energy
is the only constant of motion in a non-integrable system
; such systems are termed chaotic. In general, a classical mechanical system can be quantized
only if it is integrable; as of 2006, there is no known consistent method for quantizing chaotic dynamical systems.
coordinates (position and velocity, or position and momentum) and time that is constant throughout a trajectory. A subset of the constants of motion are the integrals of motion, defined as any functions of only the phase-space coordinates that are constant along an orbit. Every integral of motion is a constant of motion, but the converse is not true because a constant of motion may depend on time. Examples of integrals of motion are the angular momentum vector,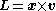
, or a Hamiltonian without time dependence, such as 
. An example of a function that is a constant of motion but not an integral of motion would be the function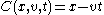 
for an object moving at a constant speed in one dimension.
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, a constant of motion is a quantity that is conserved
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
, rather than a physical constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
(which would require extra constraint forces). Common examples include energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
, linear momentum, angular momentum and the Laplace–Runge–Lenz vector (for inverse-square force laws
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
).
Applications
Constants of motion are useful because they allow properties of the motion to be derived without solving the equations of motionEquation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
. In fortunate cases, even the trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
of the motion can be derived as the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of isosurface
Isosurface
An isosurface is a three-dimensional analog of an isoline. It is a surface that represents points of a constant value within a volume of space; in other words, it is a level set of a continuous function whose domain is 3D-space.Isosurfaces are normally displayed using computer graphics, and are...
s corresponding to the constants of motion. For example, Poinsot's construction shows that the torque-free rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
is the intersection of a sphere (conservation of total angular momentum) and an ellipsoid (conservation of energy), a trajectory that might be otherwise hard to derive and visualize. Therefore, the identification of constants of motion is an important objective in mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
.
Methods for identifying constants of motion
There are several methods for identifying constants of motion.- The simplest but least systematic approach is the intuitive ("psychic") derivation, in which a quantity is hypothesized to be constant (perhaps because of experimental dataExperimental dataExperimental data in science is data produced by a measurement, test method, experimental design or quasi-experimental design. In clinical research any data produced as a result of clinical trial...
) and later shown mathematically to be conserved throughout the motion.
- The Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s provide a commonly used and straightforward method for identifying constants of motion, particularly when the HamiltonianHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
adopts recognizable functional forms in orthogonal coordinatesOrthogonal coordinatesIn mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
- Another approach is to recognize that a conserved quantityConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
corresponds to a symmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
. Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
provides a systematic way of deriving such quantities from the symmetry. For example, conservation of energyConservation of energyThe nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
results from the invariance of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
under shifts in the origin of timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, conservation of linear momentum results from the invariance of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
under shifts in the origin of spaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
(translational symmetry) and conservation of angular momentum results from the invariance of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
under rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s. The converse is also true; every symmetry of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
corresponds to a constant of motion, often called a conserved charge or current.
- A quantity
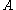is conserved if it is not explicitly time-dependent and if its Poisson bracketPoisson bracketIn mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
with the HamiltonianHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is zero
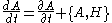
Another useful result is Poisson's theorem, which states that if two quantities
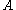and 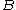are constants of motion, so is their Poisson bracket 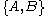.A system with n degrees of freedom, and n constants of motion, such that the Poisson bracket of any pair of constants of motion vanishes, is known as a completely integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
. Such a collection of constants of motion are said to be in involution with each other.
In quantum mechanics
An observable quantity Q will be a constant of motion if it commutesCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
with the hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, H, and it does not itself depend explicitly on time. This is because
Where
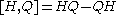
is the commutator relation.
Derivation
Say there is some observable quantity Q which depends on position, momentum and time,
And also, that there is a wave function which obeys Schrödinger's equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
Taking the time derivative of the expectation value of Q requires use of the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, and results in
|
|
|-
|
|
|-
|
|
|-
|
|
|-
|
|
|}
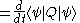
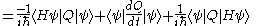
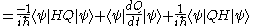
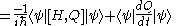
So finally,
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
|}
Comment
For an arbitrary state of a Quantum Mechanical system, if H and Q commute, i.e. if
and Q is not explicitly dependent on time , then
But if
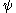is an eigenstate of Hamiltonian, then even if
provided Q is not explicitly dependent on time.
Derivation
||-
|
|}
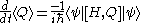
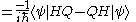
Since
 |
This is the reason why Eigen states of Hamiltonian are also called as stationary states.
Relevance for quantum chaos
In general, an integrable systemIntegrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
has constants of motion other than the energy. By contrast, energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is the only constant of motion in a non-integrable system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
; such systems are termed chaotic. In general, a classical mechanical system can be quantized
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
only if it is integrable; as of 2006, there is no known consistent method for quantizing chaotic dynamical systems.
Integral of motion
A constant of motion may be defined in a given force field as any function of phase-spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
coordinates (position and velocity, or position and momentum) and time that is constant throughout a trajectory. A subset of the constants of motion are the integrals of motion, defined as any functions of only the phase-space coordinates that are constant along an orbit. Every integral of motion is a constant of motion, but the converse is not true because a constant of motion may depend on time. Examples of integrals of motion are the angular momentum vector,
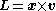, or a Hamiltonian without time dependence, such as . An example of a function that is a constant of motion but not an integral of motion would be the function 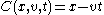for an object moving at a constant speed in one dimension.