Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal

Orthogonality

Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...

 to the velocity of the body, toward the instantaneous center of curvature

Osculating circle

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...

 of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens. Isaac Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

's description was: "A centripetal force is that by which bodies are drawn or impelled, or in any way tend, towards a point as to a center."
The magnitude of the centripetal force on an object of mass m moving at a speed v along a path with radius of curvature

Osculating circle

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...

 r is:

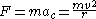
where 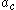is the centripetal acceleration.
The direction of the force is toward the center of the circle in which the object is moving, or the osculating circle

Osculating circle

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...

, the circle that best fits the local path of the object, if the path is not circular.
This force is also sometimes written in terms of the angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

 ω of the object about the center of the circle:


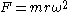
Expressed using the period for one revolution of the circle, T, the equation becomes:

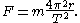
For a satellite

Satellite

In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....

 in orbit

Orbit

In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...

 around a planet

Planet

A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...

, the centripetal force is supplied by gravity.