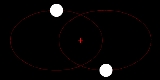
Two-body problem
Encyclopedia
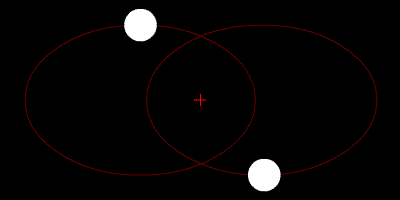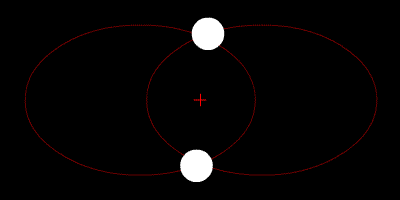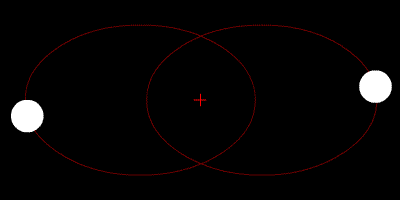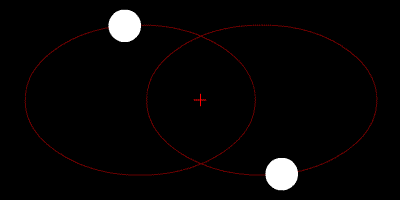
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
orbiting a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
, a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
orbiting a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
, two star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s orbiting each other (a binary star
Binary star
A binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
), and a classical electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
orbiting an atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
(although to solve this system correctly a quantum mechanical approach must be used).
The two-body problem can be re-formulated as two independent one-body problems, a trivial one and one that involves solving for the motion of one particle in an external potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
. Since many one-body problems can be solved exactly, the corresponding two-body problem can also be solved. By contrast, the three-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
(and, more generally, the n-body problem for n ≥ 3) cannot be solved, except in special cases.
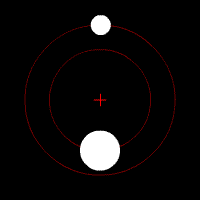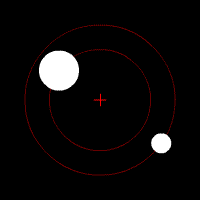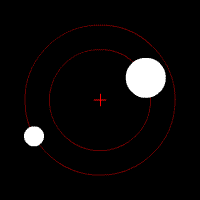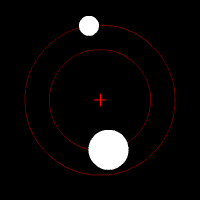
Reduction to two independent, one-body problems
Let x1 and x2 be the positions of the two bodies, and m1 and m2 be their masses. The goal is to determine the trajectories x1(t) and x2(t) for all times t, given the initial positions x1(t = 0) and x2(t = 0) and the initial velocities v1(t = 0) and v2(t = 0).When applied to the two masses, Newton's second law states that

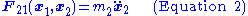
where F12 is the force on mass 1 due to its interactions with mass 2, and F21 is the force on mass 2 due to its interactions with mass 1.
Adding and subtracting these two equations decouples them into two one-body problems, which can be solved independently. Adding equations (1) and (2) results in an equation describing the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
(barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
) motion. By contrast, subtracting equation (2) from equation (1) results in an equation that describes how the vector r = x1 − x2 between the masses changes with time. The solutions of these independent one-body problems can be combined to obtain the solutions for the trajectories x1(t) and x2(t).
Center of mass motion (1st one-body problem)
Addition of the force equations (1) and (2) yields
where we have used Newton's third law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
F12 = −F21 and where
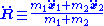
 is the position of the center of mass
is the position of the center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
(barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
) of the system.
The resulting equation:
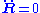
shows that the velocity V = dR/dt of the center of mass is constant, from which follows that the total momentum m1 v1 + m2 v2 is also constant (conservation of momentum). Hence, the position R (t) of the center of mass can be determined at all times from the initial positions and velocities.
Displacement vector motion (2nd one-body problem)
Dividing both force equations by the respective masses, subtracting the second equation from the first and rearranging gives the equation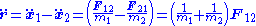
where we have again used Newton's third law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
F12 = −F21 and where r is the displacement vector
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
from mass 2 to mass 1, as defined above.
The force between the two objects, which originates in the two objects, should only be a function of their separation r and not of their absolute positions x1 and x2; otherwise, there would not be translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
, and the laws of physics would have to change from place to place. The subtracted equation can therefore be written:
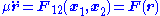
where
 is the reduced mass
is the reduced massReduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
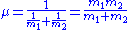
Solving the equation for r(t) is the key to the two-body problem; general solution methods are described below.
Once R (t) and r(t) have been determined, the original trajectories may be obtained

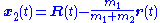
as may be verified by substituting the definitions of R and r into the right-hand sides of these two equations.
Two-body motion is planar
The motion of two bodies with respect to each other always lies in a plane (in the center of mass frame). Defining the linear momentum p and the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
L by the equations
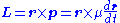
the rate of change of the angular momentum L equals the net torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
N

and using the property of the vector cross product that v × w = 0 for any vectors v and w pointing in the same direction,
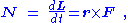
with F = μ d 2r / dt 2.
Introducing the assumption (true of most physical forces, as they obey Newton's strong third law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
) that the force between two particles acts along the line between their positions, it follows that r × F = 0 and the angular momentum vector L is constant (conserved). Therefore, the displacement vector r and its velocity v are always in the plane perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the constant vector L.
Central forces
For many physical problems, the force F(r) is a central force, i.e., it is of the form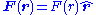
where r = |r| and r̂ = r/r is the corresponding unit vector. We now have:
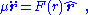
where F(r) is negative in the case of an attractive force.
Work
The total work done in a given time interval by the forces exerted by two bodies on each other is the same as the work done by one force applied to the total relative displacement.See also
- Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
- Energy driftEnergy driftIn molecular dynamics, orbit, and particle simulations, energy drift is the gradual change in the total energy of a closed system. According to the laws of mechanics, the energy should be a constant of motion and should not change...
- Equation of the centerEquation of the centerFor further closely related mathematical developments see also Two-body problem, also Gravitational two-body problem, also Kepler orbit, and Kepler problem...
- Euler's three-body problemEuler's three-body problemIn physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
- Gravitational two-body problemGravitational two-body problemFor further relevant mathematical developments see also Two-body problem, also Kepler orbit, and Kepler problem, and Equation of the center – Analytical expansions...
- Kepler problemKepler problemIn classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
- n-body problemN-body problemThe n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
- Virial theorem
External links
- Two-body problem at Eric Weisstein's World of PhysicsScienceWorldScienceWorld, also known as Eric Weisstein's World of Science, is a Web site that opened to the general public in January 2002. As of November 2007, ScienceWorld includes more than 4,000 entries in fields of science including astronomy, chemistry, physics, as well as biographies of many scientists...

