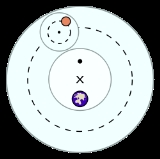
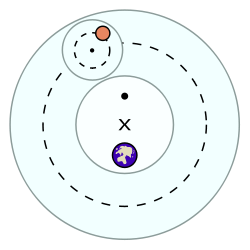
Deferent and epicycle
Encyclopedia
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, the epicycle (literally: on the circle in Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
) was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, and planets. It was first proposed by Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
at the end of the 3rd century BC and formalized by Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
of the Thebaid
Thebaid
The Thebaid or Thebais is the region of ancient Egypt containing the thirteen southernmost nomes of Upper Egypt, from Abydos to Aswan. It acquired its name from its proximity to the ancient Egyptian capital of Thebes....
in his 2nd-century AD astronomical treatise the Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
. In particular it explained the retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from Earth.
It is called Ptolemaic after the Greek astronomer Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
, although it had been developed by previous Greek astronomers such as Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
and Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
of Rhodes, who used it extensively, almost five centuries before Ptolemy. Epicyclical motion is used in the Antikythera Mechanism
Antikythera mechanism
The Antikythera mechanism is an ancient mechanical computer designed to calculate astronomical positions. It was recovered in 1900–1901 from the Antikythera wreck. Its significance and complexity were not understood until decades later. Its time of construction is now estimated between 150 and 100...
, an ancient Greek astronomical device for computing the phase and position of the Moon using four gears, two of them engaged in an eccentric way that closely approximates Kepler's second law, i.e. the Moon moves faster at perigee and slower at apogee.
In the Ptolemaic system, the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s are assumed to move in a small circle called an epicycle, which in turn moves along a larger circle called a deferent. Both circles rotate eastward and are roughly parallel to the plane of the Sun's orbit (ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
). The orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s of planets in this system are epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
s.
Despite the fact that the Ptolemaic system is considered geocentric, the planets' motion was not thought to be actually centered on the Earth. Instead, the deferent was centered on a point halfway between the Earth and another point called the equant
Equant
Equant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of heavenly bodies....
. The epicycle, meanwhile, rotated and revolved along the deferent with uniform motion. The rate at which the planet moved on the epicycle was fixed such that the angle between the center of the epicycle and the planet was the same as the angle between the earth and the sun.
Ptolemy did not predict the relative sizes of the planetary deferents in the Almagest. All of his calculations were done with respect to a normalized deferent. This is not to say that he believed the planets were all equidistant. He did guess at an ordering of the planets. Later he calculated their distances in the Planetary Hypotheses.
For superior planets the planet would typically move through in the night sky slower than the stars. Each night the planet would "lag" a little behind the star. This is prograde motion. Occasionally, near opposition, the planet would appear to move through in the night sky faster than the stars. This is retrograde motion. Ptolemy's model, in part, sought to explain this behavior.
The inferior planets were always observed to be near the sun, appearing only shortly before sunrise or shortly after sunset. To accommodate this, Ptolemy's model fixed the motion of Mercury and Venus so that the line from the equant point to the center of the epicycle was always parallel to the earth-sun line.
History
When ancient astronomers viewed the sky, they saw the Sun, Moon, and stars moving overhead in a regular fashion. They also saw the "wanderers" or "planetai" (our planetPlanet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s). The regularity in the motions of the wandering bodies suggested that their positions might be predictable.
The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions.
The ancients worked from a geocentric perspective for the simple reason that the Earth was where they stood and observed the sky, and it is the sky which appears to move while the ground seems still and steady underfoot. Some Greek astronomers (e.g., Aristarchus of Samos
Aristarchus of Samos
Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...
) speculated that the planets (Earth included) orbited the Sun, but the optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
(and the specific mathematics – Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's Law of Gravitation for example) necessary to provide data that would convincingly support the heliocentric model did not exist in Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
's time and would not come around for over fifteen hundred years after his death. Furthermore, Aristotelian Physics
Aristotelian physics
Aristotelian Physics the natural sciences, are described in the works of the Greek philosopher Aristotle . In the Physics, Aristotle established general principles of change that govern all natural bodies; both living and inanimate, celestial and terrestrial—including all motion, change in respect...
was not designed with these sorts of calculations in mind, and Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
's philosophy regarding the heavens was entirely at odds with the concept of heliocentrism. It was not until Galileo Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
observed the moons of Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
on January 7, 1610, and the phases of Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
in September, 1610 that the heliocentric model began to receive broad support among astronomers, who also came to accept the notion that the planets are individual worlds orbiting the Sun (that is, that Earth is a planet and is one among several.) The effects the telescope had on astronomy came quickly and were both controversial and profound. Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
was able to formulate his famous three laws of planetary motion, which described the orbits of the planets in our solar system with incredible accuracy; Kepler's three laws are still taught today in University physics and astronomy classes, and the wording of these laws has not changed since Kepler first formulated them four hundred years ago.
The apparent motion of the heavenly bodies with respect to time is cyclical
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
in nature. Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
realized that this cyclical variation could be represented visually by circles, or epicycles (mini circular orbits), revolving on larger circular orbits, or deferents. Deferents and epicycles in the ancient models did not represent orbits in the modern sense. The ancients did not know about orbits.
Claudius Ptolemy refined the deferent/epicycle concept and introduced the equant
Equant
Equant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of heavenly bodies....
as a mechanism for accounting for velocity variations in the motions of the planets. The empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
methodology he developed proved to be extraordinarily accurate for its day and was still in use at the time of Copernicus and Kepler.
Owen Gingerich
Owen Gingerich
Dr. Owen Jay Gingerich is a former Research Professor of Astronomy and of the History of Science at Harvard University, and a senior astronomer emeritus at the Smithsonian Astrophysical Observatory...
describes a planetary conjunction that occurred in 1504 that was apparently observed by Copernicus. In notes bound with his copy of the Alfonsine Tables, Copernicus commented that "Mars surpasses the numbers by more than two degrees. Saturn is surpassed by the numbers by one and a half degrees." Using modern computer programs, Gingerich discovered that, at the time of the conjunction, Saturn indeed lagged behind the tables by a degree and a half and Mars led the predictions by nearly two degrees. Moreover, he found that Ptolemy's predictions for Jupiter at the same time were quite accurate. Copernicus and his contemporaries were therefore using Ptolemy's methods and finding them trustworthy well over a thousand years after Ptolemy's original work was published.
When Copernicus transformed Earth-based observations to heliocentric coordinates, he was confronted with an entirely new problem. The Sun-centered positions displayed a cyclical motion with respect to time but without retrograde loops in the case of the outer planets. In principle, the heliocentric motion was simpler but with new subtleties due to the yet-to-be-discovered elliptical shape of the orbits. Another complication was caused by a problem that Copernicus never solved: correctly accounting for the motion of the Earth in the coordinate transformation. In keeping with past practice, Copernicus used the deferent/epicycle model in his theory but his epicycles were small and were called "epicyclets".
In the Ptolemaic system the models for each of the planets were different and so it was with Copernicus' initial models. As he worked through the mathematics, however, Copernicus discovered that his models could be combined in a unified system. Furthermore, if they were scaled so that Earth's orbit was the same in all of them, the ordering of the planets we recognize today easily followed from the math. Mercury orbited closest to the Sun and the rest of the planets fell into place in order outward, arranged in distance by their periods of revolution.
Although Copernicus' models reduced the magnitude of the epicycles considerably, whether they were simpler than Ptolemy's is moot. Copernicus eliminated Ptolemy's somewhat-maligned equant but at a cost of additional epicycles. Various 16th-century books based on Ptolemy and Copernicus use about equal numbers of epicycles. The idea that Copernicus used only 34 circles in his system comes from his own statement in a preliminary unpublished sketch called the Commentariolus. By the time he published De revolutionibus orbium coelestium
De revolutionibus orbium coelestium
De revolutionibus orbium coelestium is the seminal work on the heliocentric theory of the Renaissance astronomer Nicolaus Copernicus...
, he had added more circles. Counting the total number is difficult, but estimates are that he created a system just as complicated, or even more so. The popular total of about 80 circles for the Ptolemaic system seems to have appeared in 1898. It may have been inspired by the non-Ptolemaic system of Girolamo Fracastoro
Girolamo Fracastoro
Girolamo Fracastoro was an Italian physician, poet, and scholar in mathematics, geography and astronomy. Fracastoro subscribed to the philosophy of atomism, and rejected appeals to hidden causes in scientific investigation....
, who used either 77 or 79 orbs in his system inspired by Eudoxus of Cnidus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
.
Copernicus' theory was at least as accurate as Ptolemy's but never achieved the stature and recognition of Ptolemy's theory. What was needed was Kepler's elliptical theory, not published till 1609. Copernicus' work provided explanations for phenomena like retrograde motion, but really didn't prove that the planets actually orbited the Sun.
Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today and might still be in use had Isaac Newton not invented Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and the Calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
The first planetary model without any epicycles was that of Ibn Bajjah
Ibn Bajjah
Abū-Bakr Muhammad ibn Yahya ibn al-Sāyigh , known as Ibn Bājjah , was an Andalusian polymath: an astronomer, logician, musician, philosopher, physician, physicist, psychologist, botanist, poet and scientist. He was known in the West by his Latinized name, Avempace...
(Avempace) in 12th century Andalusian Spain
Al-Andalus
Al-Andalus was the Arabic name given to a nation and territorial region also commonly referred to as Moorish Iberia. The name describes parts of the Iberian Peninsula and Septimania governed by Muslims , at various times in the period between 711 and 1492, although the territorial boundaries...
, but epicycles were not eliminated in Europe until the 17th century, when Johannes Kepler's model of elliptical orbits gradually replaced Copernicus' model based on perfect circles.
Newtonian or Classical Mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
eliminated the need for deferent/epicycle methods altogether and produced theories many times more powerful. By treating the Sun and planets as point masses and using Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, equations of motion were derived that could be solved by various means to compute predictions of planetary orbital velocities and positions. Simple two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
s, for example, can be solved analytically. More-complex n-body problem
N-body problem
The n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
s require numerical methods for solution.
The power of Newtonian mechanics to solve problems in orbital mechanics is illustrated by the discovery of Neptune
Neptune
Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times...
. Analysis of observed perturbations in the orbit of Uranus
Uranus
Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...
produced estimates of the suspected planet's position within a degree of where it was found. This could not have been accomplished with deferent/epicycle methods. Still, Newton in 1702 published Theory of the Moon's Motion which employed an epicycle and remained in use in China into the ninetheenth century. Subsequent tables based on Newton's Theory could have approached arcminute accuracy.
Epicycles on epicycles
According to one school of thought in the history of astronomy, minor imperfections in the original Ptolemaic system were discovered through observations accumulated over time. It was mistakenly believed that more levels of epicycles (circles within circles) were added to the models to match more accurately the observed planetary motions. The multiplication of epicycles is believed to have led to a nearly unworkable system by the 16th century, and that Copernicus created his heliocentric system in order to simplify the Ptolemaic astronomy of his day, thus succeeding in drastically reducing the number of circles.- With better observations additional epicycles and eccentrics were used to represent the newly observed phenomena till in the later Middle Ages the universe became a 'Sphere/With Centric and Eccentric scribbled o'er,/Cycle and Epicycle, Orb in Orb' –
As a measure of complexity, the number of circles is given as 80 for Ptolemy, versus a mere 34 for Copernicus. The highest number appeared in the Encyclopaedia Britannica on Astronomy during the 1960s, in a discussion of King Alfonso X of Castile
Alfonso X of Castile
Alfonso X was a Castilian monarch who ruled as the King of Castile, León and Galicia from 1252 until his death...
's interest in astronomy during the 13th century. (Alfonso is credited with commissioning the Alfonsine Tables
Alfonsine tables
The Alfonsine tables provided data for computing the position of the Sun, Moon and planets relative to the fixed stars....
.)
- By this time each planet had been provided with from 40 to 60 epicycles to represent after a fashion its complex movement among the stars. Amazed at the difficulty of the project, Alfonso is credited with the remark that had he been present at the Creation he might have given excellent advice.
As it turns out, a major difficulty with this epicycles-on-epicycles theory is that historians examining books on Ptolemaic astronomy from the Middle Ages and the Renaissance have found absolutely no trace of multiple epicycles being used for each planet. The Alfonsine Tables, for instance, were apparently computed using Ptolemy's original unadorned methods.
Another problem is that the models themselves discouraged tinkering. In a deferent/epicycle model, the parts of the whole are interrelated. A change in a parameter to improve the fit in one place would throw off the fit somewhere else. Ptolemy's model is probably optimal in this regard. On the whole it gave good results but missed a little here and there. Experienced astronomers would have recognized these shortcomings and allowed for them.
Slang for bad science
In part, due to misunderstandings about how deferent/epicycle models worked, "adding epicycles" has come to be used as a derogatory comment in modern scientific discussion. The term might be used, for example, to describe continuing to try to adjust a theory to make its predictions match the facts. According to this notion, epicycles are regarded by some as the paradigmatic example of Bad Science. Part of the problem may be due to the misconception of the epicycle as an explanation of a body's motion rather than merely a description. Toomer explains as follows,- "Whereas we use 'hypothesis' to denote a tentative theory which is still to be verified, Ptolemy usually means by ύπόθεσις something more like 'model', 'system of explanation', often indeed referring to 'the hypotheses which we have demonstrated'."
Legacy
Much of the content of the epicycle system was taken over by its successors and is still in use today. Some of the terms used in modern astronomy are anomalyTrue anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
, equation
Equation of time
The equation of time is the difference between apparent solar time and mean solar time. At any given instant, this difference will be the same for every observer...
, mean motion
Mean motion
Mean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
, eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
, apogee and perigee
Perigee
Perigee is the point at which an object makes its closest approach to the Earth.. Often the term is used in a broader sense to define the point in an orbit where the orbiting body is closest to the body it orbits. The opposite is the apogee, the farthest or highest point.The Greek prefix "peri"...
.
Mathematical formalism
According to the historian of scienceHistory of science
The history of science is the study of the historical development of human understandings of the natural world and the domains of the social sciences....
Norwood Russell Hanson:
There is no bilaterally-symmetrical, nor excentrically-periodic curve used in any branch of astrophysics or observational astronomy which could not be smoothly plotted as the resultant motion of a point turning within a constellation of epicycles, finite in number, revolving around a fixed deferent.Any path—periodic or not, closed or open—can be represented with an infinite number of epicycles.
This is because epicycles can be represented as a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
; so, with a large number epicycles, very complicated paths can be represented in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
Let the complex number
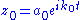 ,
,where
 and
and 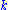 are constants,
are constants, 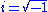 is an imaginary number
is an imaginary numberImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, and
 is time, correspond to a deferent centered on the origin of the complex plane
is time, correspond to a deferent centered on the origin of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and revolving with a radius
 and angular velocity
and angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
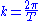 ,
,where
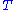 is the period
is the periodPeriod
Period may mean a full stop: a punctuation in American-English.Period or periodic may also refer to:-Science:* Orbital period, a concept in astronomy...
.
If
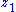 is the path of an epicycle, then the deferent plus epicycle is represented as the sum
is the path of an epicycle, then the deferent plus epicycle is represented as the sum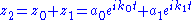 .
.Generalizing to
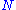 epicycles yields
epicycles yields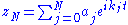 ,
,which is a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. Finding the coefficients
 to represent a time-dependent path in the complex plane
to represent a time-dependent path in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
,
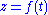 , is the goal of reproducing an orbit with deferent and epicycles, and this is a way of "saving the phenomena" (σώζειν τα φαινόμενα).
, is the goal of reproducing an orbit with deferent and epicycles, and this is a way of "saving the phenomena" (σώζειν τα φαινόμενα).Pertinent to the Copernican Revolution
Copernican Revolution
The Copernican Revolution refers to the paradigm shift away from the Ptolemaic model of the heavens, which postulated the Earth at the center of the galaxy, towards the heliocentric model with the Sun at the center of our Solar System...
debate of "saving the phenomena" versus offering explanations, one can understand why Thomas Aquinas, in the 13th century, wrote:
Reason may be employed in two ways to establish a point: firstly, for the purpose of furnishing sufficient proof of some principle [...]. Reason is employed in another way, not as furnishing a sufficient proof of a principle, but as confirming an already established principle, by showing the congruity of its results, as in astronomy the theory of eccentrics and epicyclesDeferent and epicycleIn the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
is considered as established, because thereby the sensible appearances of the heavenly movements can be explained; not, however, as if this proof were sufficient, forasmuch as some other theory might explain them. [...]
External links
- Ptolemaic System – at Rice University's Galileo Project
Animated illustrations
- Java simulation of the Ptolemaic System – at Paul Stoddard's Animated Virtual Planetarium, Northern Illinois University
- Epicycle and Deferent Demo – at Rosemary Kennett's website at the University of Syracuse
- A flash animation showing epicycles with adjustable parameters and presets for various planets.
- An Applet showing the principle of the epicycle, with a side-by-side comparison of the geocentric and heliocentric models.

