Methods of contour integration - AbsoluteAstronomy.com

In the mathematical field of complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, contour integration is a method of evaluating certain integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

s along paths in the complex plane.

Contour integration is closely related to the calculus of residues

Residue theorem

The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...

, a methodology of complex analysis

Complex analysis

.

One use for contour integrals is the evaluation of integrals along the real line that are not readily found by using only real variable methods.

Contour integration methods include

direct integration of a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

-valued function along a curve in the complex plane (a contour)
application of the Cauchy integral formula
application of the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...

.

One method can be used, or a combination of these methods, or various limiting processes, for the purpose of finding these integrals or sums.

Direct methods

Direct methods involve the calculation of the integral by means of methods similar to those in calculating line integrals in several-variable calculus. This means that we use the following method:

parametrizing the contour

The contour is parametrized by a differentiable complex-valued function of real variables, or the contour is broken up into pieces and parametrized separately

substitution of the parametrization into the integrand

Substituting the parametrization into the integrand transforms the integral into an integral of one real variable.

direct evaluation

The integral is evaluated in a method akin to a real-variable integral.

Example

A fundamental result in complex analysis is that the contour integral of z⁻¹ is 2πi, where the path of the contour is taken to be the unit circle traversed counterclockwise (or any Jordan curve about 0). In the case of the unit circle there is a direct method to evaluate the integral

In evaluating this integral, use the unit circle |z| = 1 as contour, parametrized by z(t) = e^it, with t ∈ [0, 2π], then dz / dt = i e^it and

which is the value of the integral.

Applications of integral theorems

Applications of integral theorems are also often used to evaluate the contour integral along a contour, which means that the real-valued integral is calculated simultaneously along with calculating the contour integral.

Integral theorems such as the Cauchy integral formula or residue theorem

Residue theorem

are generally used in the following method:

a specific contour is chosen:

The contour is chosen so that the contour follows the part of the complex plane that describes the real-valued integral, and also encloses singularities of the integrand so application of the Cauchy integral formula or residue theorem

Residue theorem

is possible

application of the Cauchy–Goursat theorem

The integral is reduced to only an integration around a small circle about each pole.

application of the Cauchy integral formula or residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...

Application of these integral formula gives us a value for the integral around the whole of the contour.

division of the contour into a contour along the real part and imaginary part

The whole of the contour can be divided into the contour that follows the part of the complex plane that describes the real-valued integral as chosen before (call it R), and the integral that crosses the complex plane (call it I). The integral over the whole of the contour is the sum of the integral over each of these contours.

demonstration that the integral that crosses the complex plane plays no part in the sum

If the integral I can be shown to be zero, or if the real-valued integral that is sought is improper, then if we demonstrate that the integral I as described above tends to 0, the integral along R will tend to the integral around the contour R + I.

conclusion

If we can show the above step, then we can directly calculate R, the real-valued integral.

Example (I)

Consider

To evaluate this integral, we look at the complex-valued function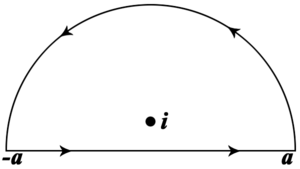

which has singularities at i and −i. However, we will want to choose a contour that will enclose the real-valued integral, so we choose a semicircle like the one shown on the left, which we will let expand as to contain the whole real axis (a will tend to infinity). Call this contour C.

Now, there are two ways of proceeding, using the Cauchy integral formula or by the method of residues.

Using the Cauchy integral formula

Note that:

thus

Furthermore observe that

Since the only singularity in the contour is the one at i, then we can write

which puts the function in the form for direct application of the formula.
Then, by Cauchy's integral formula,

(We take the first derivative, in the above steps, because the pole is a second-order pole. That is, is taken to the second power, so we employ the first derivative of ƒ(z). If it were taken to the third power, we would use the second derivative and divide by 2!, etc. The case of to the first power corresponds to a zero order derivative—just ƒ(x) itself.)

If we call the arc of the semicircle Arc, we need to show that the integral over Arc tends to zero as a tends to infinity — using the estimation lemma

Estimation lemma

In mathematics, the estimation lemma gives an upper bound for a contour integral. If f is a complex-valued, continuous function on the contour \Gamma and if its absolute value |f| is bounded by a constant M for all z on \Gamma, then...

where M is an upper bound on |ƒ(z)| along the Arc and L the length of Arc. Now,

Using the method of residues

Consider the Laurent series

Laurent series

In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...

of f(z) about i, the only singularity we need to consider. We then have

(See Sample Laurent Calculation from Laurent series

Laurent series

for the derivation of this series.)

It is clear by inspection that the residue is −i/4 (to see this, imagine that the above equation were multiplied by z − i, then both sides integrated via the Cauchy integral formula—only the second term would integrate to a non-zero quantity), so, by the residue theorem

Residue theorem

, we have

Thus we get the same result as before.

Contour note

As an aside, a question can arise whether we do not take the semicircle to include the other singularity, enclosing −i. To have the integral along the real axis moving in the correct direction, the contour must travel clockwise, i.e., in a negative direction, reversing the sign of the integral overall.

This does not affect the use of the method of residues by series.

Example (II) – Cauchy distribution

The integral

(which arises in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

as (a scalar multiple
of) the characteristic function

Characteristic function (probability theory)

In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...

of the Cauchy distribution

Cauchy distribution

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

)
resists the techniques of elementary calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

. We will
evaluate it by expressing it as a limit of contour integrals
along the contour C that goes along the real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

line from −a to a and then counterclockwise along
a semicircle centered at 0 from a to −a. Take
a to be greater than 1, so that the imaginary

Imaginary number

An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...

unit i is enclosed within the curve. The contour integral is

Since e^itz is an entire function

Entire function

In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

(having no singularities

Mathematical singularity

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

at any point in the complex plane), this function has
singularities only where the denominator
z² + 1 is zero. Since
z² + 1 = (z + i)(z − i),
that happens only where z = i or z = −i.
Only one of those points is in the region bounded by this
contour. The residue

Residue (complex analysis)

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...

of
f(z) at z = i is

According to the residue theorem

Residue theorem

, then, we have

The contour C may be split into a "straight"
part and a curved arc, so that

and thus

It can be shown that if t > 0 then

Therefore if t > 0 then

A similar argument with an arc that winds around −i
rather than i shows that if t < 0 then

and finally we have this:

(If t = 0 then the integral yields immediately to real-valued calculus methods and its value is π.)

Example (III) – trigonometric integrals

Certain substitutions can be made to integrals involving trigonometric functions, so the integral is transformed into a rational function of a complex variable and then the above methods can be used in order to evaluate the integral.

As an example, consider

We seek to make a substitution of z = e^it.

Now, recall

and

Taking C to be the unit circle, we substitute to get:

We use the Cauchy integral formula. Factorize the denominator:

The singularities then to be considered are at 3^−1/2i, −3^−1/2i. We can now reduce the integral:

where C₁ is a small circle about 3^−1/2i, and C₂ is a small circle about −3^−1/2i. We can now apply the formula:

Example (IIIa) trigonometric integrals, the general procedure

The above method may be applied to all integrals of the type

where P and Q are polynomials, i.e. a rational function in trigonometric terms is being integrated.

The trick is to use the substitution

where

and hence

This substitution maps the interval

to the unit circle. Furthermore,

and

so that a rational function ƒ(z) in z results from the substitution, and the integral becomes

which is in turn computed by summing the residues of ƒ(z) inside the unit circle.

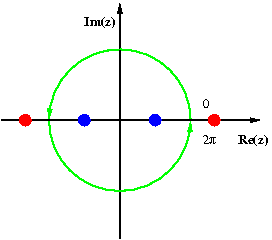
The image at right illustrates this for

which we now compute. The first step is to recognize that

The substitution yields

The poles of this function are at 1 ± √2 and −1 ± √2. Of these, 1 + √2 and −1 −√2 are outside the unit circle (shown in red, not to scale), whereas 1 − √2 and −1 + √2 are inside the unit circle (shown in blue). The corresponding residues are both equal to −i√2/16, so that the value of the integral is

Example (IV) – branch cuts

Consider

We can begin by formulating the complex integral

We can use the Cauchy integral formula or residue theorem again to obtain the relevant residues. However, the important thing to note is that z^1/2 = e^1/2·Log(z), so z^1/2 has a branch cut. This affects our choice of the contour C. Normally the logarithm branch cut is defined as the negative real axis, however, this makes the calculation of the integral slightly more complex, so we define it to be the positive real axis.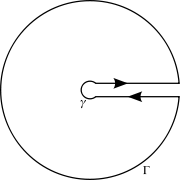

Then, we use the so-called keyhole contour, which consists of a small circle about the origin of radius ε say, extending to a line segment parallel and close to the positive real axis but not touching it, to an almost full circle, returning to a line segment parallel, close, and below the positive real axis in the negative sense, returning to the small circle in the middle.

Note that z = −2 and z = −4 are inside the big circle. These are the two remaining poles, derivable by factoring the denominator of the integrand. The branch point at z = 0 was avoided by detouring around the origin.

Let γ be the small circle of radius ε, Γ the larger, with radius r, then

Since z^1/2 = e^1/2 Log(z), on the contour outside the branch cut, we have gained 2π in argument along γ (by Euler's Identity,

represents the unit vector, which therefore has

as its log. This

is what is meant by the argument of z. The coefficient of 1/2 forces us to use 2 times

), so

simplifying,

and then

It can be shown that the integrals over Γ and γ both tend to zero as ε tends to zero and R tends to infinity, by an estimation argument above. Thus, then,

By using the residue theorem or the Cauchy integral formula (first employing the partial fractions method to derive a sum of two simple contour integrals) one obtains

Example (V) – the square of the logarithm

This section treats a type of integral of which

is an example.

To calculate this integral, one uses the function

and the branch of the logarithm corresponding to

.

We will calculate the integral of ƒ(z) along the keyhole contour shown at right. As it turns out this integral is a multiple of the initial integral that we wish to calculate.

Let R be the radius of the large circle, and r the radius of the small one. We will denote the upper line by M, and the lower line by N. As before we take the limit when R goes to infinity and r to zero. The two contributions from the two circles vanish. For example, one has the following upper bound with the ML-lemma:

By the Cauchy residue theorem we thus have

It remains to calculate the contributions of M and N. We set

on M and

on N, with

This gives

To conclude, one observes that

and thus

which gives

Example (VI) – logarithms and the residue at infinity

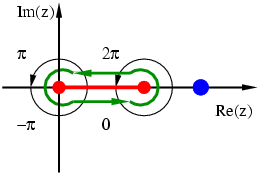
We seek to evaluate

This requires a close study of

We will construct f(z) so that it has a branch cut on [0, 3],
shown in red in the diagram. To do this, we choose two branches of the logarithm, setting

and

The cut of z^3/4 is therefore

and the cut of

.
It is easy to see that the cut of the product of the two, i.e.

, is

, because f(z) is actually continuous across

This is because when

and we approach
the cut from above, f(z) has the value

When we approach from below, f(z) has the value

But

so that we have continuity across the cut. This is illustrated in the diagram, where the two black oriented circles are labelled
with the corresponding value of the argument of the logarithm used in

and

We will use the contour shown in green in the diagram.
To do this we must compute the value of ƒ(z) along the line segments just above and just below the cut.

Let