
Functional integration
Encyclopedia
Functional integration is a collection of results in mathematics
and physics
where the domain
of an integral
is no longer a region of space
, but a space of functions
. Functional integrals arise in probability
, in the study of partial differential equations and in Feynman's approach
to the quantum mechanics
of particles and fields.
In an ordinary integral
there is a function to be integrated—the integrand—and a region of space over which to integrate the function—the domain of integration. The process of integration consists of adding the values of the integrand at each point of the domain of integration. Making this procedure rigorous requires a limiting procedure, where the domain of integration is divided into smaller and smaller regions. For each small region the value of the integrand cannot vary much so it may be replaced by a single value. In a functional integral the domain of integration is a space of functions. For each function the integrand returns a value to add up. Making this procedure rigorous poses challenges that are the topic of research in the beginning of the 21st century.
Functional integration was developed by P. J. Daniell
in a paper of 1919 and Wiener
in a series of studies culminating in his papers of 1921 on Brownian motion
. They developed a rigorous method —now known as the Wiener measure— for assigning a probability to a particle's random path. Feynman
developed another functional integral, the path integral
, useful for computing the quantum properties of systems. In Feynman's path integral, the classical notion of a unique trajectory for a particle is replaced by an infinite sum of classical paths, each weighted differently according to its classical properties.
Functional integration is central to quantization techniques in theoretical physics. The algebraic properties of functional integrals are used to develop series used to calculate properties in quantum electrodynamics
and the standard model
.
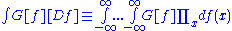
However in most cases the functions f(x) can be written in terms of an infinite series of orthogonal functions such as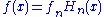 and then the definition becomes:
and then the definition becomes:
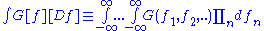
which is slightly more understandable. The integral is shown to be a functional integral with a capital D. Sometimes it is written in square brackets [Df] or D[f] to indicate f is a function.
of two functional integrals can be finite. The functional integrals that can be solved exactly usually start with the following Gaussian integral
:
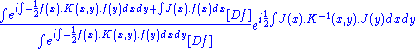
By functionally differentiating this with respect to J(x) and then setting J to 0 this becomes an exponential multiplied by a polynomial in f. For example setting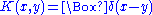 we find:
we find:
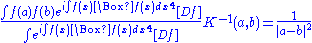
where a,b and x are 4-dimensional vectors. This comes from the formula for the propagation of a photon in quantum electrodynamics. Another useful integral is the functional delta function:
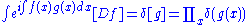
which is useful to specify constraints. Functional integrals can also be done over grasmman valued functions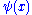 where
where 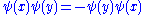 which is useful in quantum electrodynamics for calculations involving fermions.
which is useful in quantum electrodynamics for calculations involving fermions.
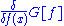
yield an integral based on a measure
; whereas the constructions following Feynman's path integral do not. Even within these two broad divisions, the integrals are not identical, that is, they are defined for different classes of functions.
a probability is assigned to a class of Brownian motion
paths. The class consists of the paths w that are known to go through a small region of space at a given time. The passage through different regions of space is assumed independent of each other and the distance between any two points of the Brownian path is assumed to be Gaussian distributed with a variance
that depends on the time t and on a diffusion constant D:
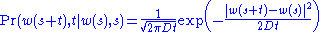
The probability for the class of paths can be found by multiplying the probabilities of starting in one region and then being at the next. The Wiener measure can be developed by considering the limit of many small regions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
where the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is no longer a region of space
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, but a space of functions
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. Functional integrals arise in probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, in the study of partial differential equations and in Feynman's approach
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
to the quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
of particles and fields.
In an ordinary integral
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
there is a function to be integrated—the integrand—and a region of space over which to integrate the function—the domain of integration. The process of integration consists of adding the values of the integrand at each point of the domain of integration. Making this procedure rigorous requires a limiting procedure, where the domain of integration is divided into smaller and smaller regions. For each small region the value of the integrand cannot vary much so it may be replaced by a single value. In a functional integral the domain of integration is a space of functions. For each function the integrand returns a value to add up. Making this procedure rigorous poses challenges that are the topic of research in the beginning of the 21st century.
Functional integration was developed by P. J. Daniell
Percy John Daniell
Percy John Daniell was a pure and applied mathematician. In a series of papers published between 1918 and 1928, he developed and expanded a generalized theory of integration and differentiation, which is today known as the Daniell integral.Daniell was born in Valparaiso, Chile. His family...
in a paper of 1919 and Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
in a series of studies culminating in his papers of 1921 on Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. They developed a rigorous method —now known as the Wiener measure— for assigning a probability to a particle's random path. Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
developed another functional integral, the path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
, useful for computing the quantum properties of systems. In Feynman's path integral, the classical notion of a unique trajectory for a particle is replaced by an infinite sum of classical paths, each weighted differently according to its classical properties.
Functional integration is central to quantization techniques in theoretical physics. The algebraic properties of functional integrals are used to develop series used to calculate properties in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
and the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
Functional Integration
Whereas normal integration sums a function, f(x), over a continuous range of values of x, functional integration sums a functional, G[f], over a continuous range of functions, f. Most functional integrals cannot be solved exactly but must be solved using perturbation methods. The formal definition is: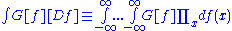
However in most cases the functions f(x) can be written in terms of an infinite series of orthogonal functions such as
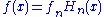 and then the definition becomes:
and then the definition becomes: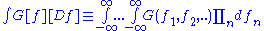
which is slightly more understandable. The integral is shown to be a functional integral with a capital D. Sometimes it is written in square brackets [Df] or D[f] to indicate f is a function.
Examples
Most functional integrals are actually infinite but the quotientQuotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of two functional integrals can be finite. The functional integrals that can be solved exactly usually start with the following Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
:
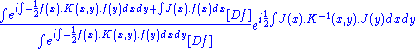
By functionally differentiating this with respect to J(x) and then setting J to 0 this becomes an exponential multiplied by a polynomial in f. For example setting
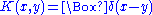 we find:
we find: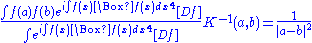
where a,b and x are 4-dimensional vectors. This comes from the formula for the propagation of a photon in quantum electrodynamics. Another useful integral is the functional delta function:
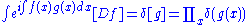
which is useful to specify constraints. Functional integrals can also be done over grasmman valued functions
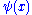 where
where 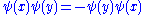 which is useful in quantum electrodynamics for calculations involving fermions.
which is useful in quantum electrodynamics for calculations involving fermions.Inverse of functional derivative
Functional integration can be thought of as the inverse operation to functional differentiation. The functional derivative of the functional G is written as: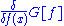
In symbolic algebra software
Most symbolic algebra packages such as Maple or Mathematica do not support functional (path) integration as standard although additional packages can be constructed for them.Approaches to path integrals
Functional integrals where the space of integration are paths (ν = 1) can be defined in many different ways. The definitions fall in two different classes: the constructions derived from Wiener's theoryWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
yield an integral based on a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
; whereas the constructions following Feynman's path integral do not. Even within these two broad divisions, the integrals are not identical, that is, they are defined for different classes of functions.
The Wiener integral
In the Wiener integralWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
a probability is assigned to a class of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
paths. The class consists of the paths w that are known to go through a small region of space at a given time. The passage through different regions of space is assumed independent of each other and the distance between any two points of the Brownian path is assumed to be Gaussian distributed with a variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
that depends on the time t and on a diffusion constant D:
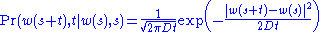
The probability for the class of paths can be found by multiplying the probabilities of starting in one region and then being at the next. The Wiener measure can be developed by considering the limit of many small regions.
- Ito and Stratonovich calculus
The Feynman integral
- Trotter formula
- The Kac idea of Wick rotations.
- Using x-dot-dot-squared or i S[x] + x-dot-squared.
- The Cartier DeWitt-Morette relies on integrators rather than measures
The Lévy integral
- Fractional quantum mechanicsFractional quantum mechanicsIn physics, fractional quantum mechanics is a generalization of standard quantum mechanics. The term fractional quantum mechanics was coined by Nick Laskin...
- Fractional Schrödinger equationFractional Schrödinger equationThe fractional Schrödinger equation is a fundamental equation of fractional quantum mechanics. It was discovered by Nick Laskin as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by...
- Lévy processLévy processIn probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
- Fractional statistical mechanics
Further reading
- Kleinert, HagenHagen KleinertHagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004); Paperback ISBN 981-238-107-4 (also available online: PDF-files) - Nick Laskin, (2000), "Fractional Quantum Mechanics," Physical Review E62: 3135-3145. Fractional Quantum Mechanics
- Nick Laskin, (2002), "Fractional Schrödinger equation," Physical Review E66: 056108 [7 pages]. Fractional Schrödinger equation
- O.G. Smolyanov, E.T.Shavgulidze. Сontinual integrals. Moscow, Moscow State University Press, 1990. (in Russian). http://lib.mexmat.ru/books/5132

