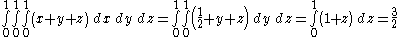Volume integral
Encyclopedia
In mathematics
— in particular, in multivariable calculus
— a volume integral refers to an integral
over a 3-dimension
al domain.
Volume
integral is a triple integral of the constant function 1, which gives the volume of the region D, that is, the integral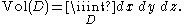
It can also mean a triple integral
within a region D in R3 of a function
and is usually written as:
A volume integral in cylindrical coordinates is
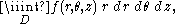
and a volume integral in spherical coordinates (using the standard convention for angles, i.e. with φ as the azimuth) has the form
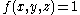over a unit cube yields the following result:
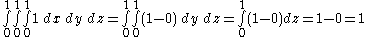
So the volume of the unit cube is 1 as expected. This is rather trivial however and a volume integral is far more powerful. For instance if we have a scalar function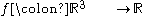
describing the density of the cube at a given point 
by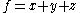 
then performing the volume integral will give the total mass of the cube:
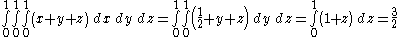
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— in particular, in multivariable calculus
Multivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
— a volume integral refers to an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over a 3-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al domain.
Volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
integral is a triple integral of the constant function 1, which gives the volume of the region D, that is, the integral
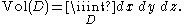
It can also mean a triple integral
Multiple integral
The multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
within a region D in R3 of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and is usually written as:A volume integral in cylindrical coordinates is
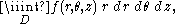
and a volume integral in spherical coordinates (using the standard convention for angles, i.e. with φ as the azimuth) has the form
Example
Integrating the function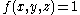 over a unit cube yields the following result: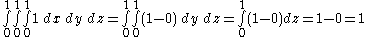So the volume of the unit cube is 1 as expected. This is rather trivial however and a volume integral is far more powerful. For instance if we have a scalar function
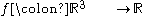describing the density of the cube at a given point by 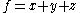then performing the volume integral will give the total mass of the cube: