
Lattice of subgroups
Encyclopedia
In mathematics
, the lattice of subgroups of a group
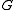 is the lattice
is the lattice
whose elements are the subgroup
s of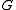 , with the partial order relation
, with the partial order relation
being set inclusion.
In this lattice, the join of two subgroups is the subgroup generated
by their union
, and the meet of two subgroups is their intersection
.
Lattice theoretic information about the lattice of subgroups can sometimes be used to infer information about the original group, an idea that goes back to the work of . For instance, as Ore proved, a group is locally cyclic
if and only if its lattice of subgroups is distributive
. Lattice-theoretic characterizations of this type also exist for solvable group
s and perfect group
s .
Dih4 has ten subgroups, counting itself and the trivial subgroup
. Five of the eight group elements generate subgroups of order two, and two others generate the same cyclic group
C4. In addition, there are two groups of the form C2×C2
, generated by pairs of order-two elements. The lattice formed by these ten subgroups is shown in the illustration.
However, neither finite subgroups nor torsion subgroups form a lattice: for instance, the free product
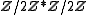 is generated by two torsion elements, but is infinite and contains elements of infinite order.
is generated by two torsion elements, but is infinite and contains elements of infinite order.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the lattice of subgroups of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
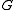 is the lattice
is the latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
whose elements are the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of
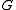 , with the partial order relation
, with the partial order relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
being set inclusion.
In this lattice, the join of two subgroups is the subgroup generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by their union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, and the meet of two subgroups is their intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
Lattice theoretic information about the lattice of subgroups can sometimes be used to infer information about the original group, an idea that goes back to the work of . For instance, as Ore proved, a group is locally cyclic
Locally cyclic group
In group theory, a locally cyclic group is a group in which every finitely generated subgroup is cyclic.-Some facts:*Every cyclic group is locally cyclic, and every locally cyclic group is abelian....
if and only if its lattice of subgroups is distributive
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
. Lattice-theoretic characterizations of this type also exist for solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s and perfect group
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
s .
Example
The dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dih4 has ten subgroups, counting itself and the trivial subgroup
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. Five of the eight group elements generate subgroups of order two, and two others generate the same cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C4. In addition, there are two groups of the form C2×C2
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
, generated by pairs of order-two elements. The lattice formed by these ten subgroups is shown in the illustration.
Characteristic lattices
Subgroups with certain properties form lattices, but other properties do not.- NilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s form a lattice, which is (part of) the content of Fitting's theoremFitting's theoremFitting's theorem is a mathematical theorem proved by Hans Fitting. It can be stated as follows:By induction it follows also that the subgroup generated by a finite collection of nilpotent normal subgroups is nilpotent. This can be used to show that the Fitting subgroup of certain types of groups ...
. - In general, for any Fitting class F, both the subnormalSubnormal subgroupIn mathematics, in the field of group theory, a subgroup H of a given group G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal in the next, beginning at H and ending at G....
F-subgroups and the normal F-subgroups form lattices. This includes the above with F the class of nilpotent groups, as well as other examples such as F the class of solvable groupSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s. A class of groups is called a Fitting class if it is closed under isomorphism, subnormal subgroups, and products of subnormal subgroups. - Central subgroups form a lattice.
However, neither finite subgroups nor torsion subgroups form a lattice: for instance, the free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
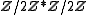 is generated by two torsion elements, but is infinite and contains elements of infinite order.
is generated by two torsion elements, but is infinite and contains elements of infinite order.See also
- Zassenhaus lemmaZassenhaus lemmaIn mathematics, the butterfly lemma or Zassenhaus lemma, named after Hans Julius Zassenhaus, is a technical result on the lattice of subgroups of a group or the lattice of submodules of a module, or more generally for any modular lattice....
, an isomorphism between certain quotients in the lattice of subgroups - Complemented groupComplemented groupIn mathematics, in the realm of group theory, the term complemented group is used in two distinct, but similar ways.In , a complemented group is one in which every subgroup has a group-theoretic complement...
, a group with a complemented latticeComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
of subgroups - Lattice theoremLattice theoremIn mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...
, a Galois connectionGalois connectionIn mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between the lattice of subgroups of a group and of its quotient - Example: Lattice of subgroups of the symmetric group S4

