Nine lemma
Encyclopedia
In mathematics
, the nine lemma is a statement about commutative diagram
s and exact sequence
s valid in any abelian category
, as well as in the category of group
s. It states: if
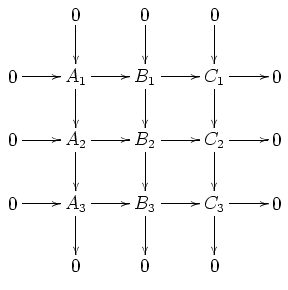
is a commutative diagram and all columns as well as the two bottom rows are exact, then the top row is exact as well. Likewise, if all columns as well as the two top rows are exact, then the bottom row is exact as well.
The nine lemma can be proved by direct diagram chasing, or by applying the snake lemma
(to the two bottom rows in the first case, and to the two top rows in the second case).
Linderholm (p. 201) offers a satirical view of the nine lemma:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the nine lemma is a statement about commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
s and exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s valid in any abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, as well as in the category of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s. It states: if
is a commutative diagram and all columns as well as the two bottom rows are exact, then the top row is exact as well. Likewise, if all columns as well as the two top rows are exact, then the bottom row is exact as well.
The nine lemma can be proved by direct diagram chasing, or by applying the snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
(to the two bottom rows in the first case, and to the two top rows in the second case).
Linderholm (p. 201) offers a satirical view of the nine lemma:
- "Draw a noughts-and-crossesTic-tac-toeTic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
board... Do not fill it in with noughts and crosses... Instead, use curved arrows... Wave your hands about in complicated patterns over this board. Make some noughts, but not in the squares; put them at both ends of the horizontal and vertical lines. Make faces. You have now proved:- (a) the Nine Lemma
- (b) the Sixteen Lemma
- (c) the Twenty-five Lemma..."