Lattice theorem
Encyclopedia
In mathematics
, the lattice theorem, sometimes referred to as the fourth isomorphism theorem
or the correspondence theorem, states that if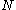
is a normal subgroup
of a group
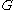, then there exists a bijection
from the set of all subgroups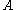
of 
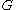such that 
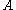contains 
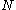, onto the set of all subgroups of the quotient group
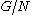. The structure of the subgroups of 
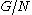is exactly the same as the structure of the subgroups of 
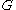containing 
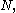with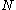 
collapsed to the identity element
.
This establishes a monotone Galois connection
between the lattice of subgroups
of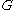
and the lattice of subgroups of 
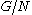, where the associated closure operator
on subgroups of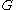
is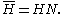 
Specifically, If
then there is a bijective map
such that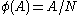
for all 
One further has that if A and B are in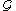
, and A' = A/N and B' = B/N, then
This list is far from exhaustive. In fact, most properties of subgroups are preserved in their images under the bijection onto subgroups of a quotient group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the lattice theorem, sometimes referred to as the fourth isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
or the correspondence theorem, states that if
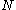is a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
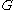, then there exists a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from the set of all subgroups
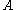of 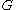such that 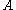contains 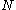, onto the set of all subgroups of the quotient groupQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
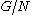. The structure of the subgroups of 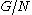is exactly the same as the structure of the subgroups of 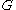containing 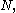with 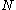collapsed to the identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
This establishes a monotone Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between the lattice of subgroups
Lattice of subgroups
In mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....
of
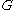and the lattice of subgroups of 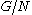, where the associated closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
on subgroups of
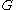is 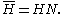Specifically, If
- G is a group,
- N is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G,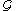
is the set of all subgroups A of G such that 
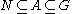, and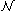
is the set of all subgroups of G/N,
then there is a bijective map
such that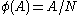 for all One further has that if A and B are in
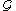, and A' = A/N and B' = B/N, then
if and only if 
;- if
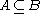then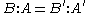 
, where B:A is the index of A in B (the number of cosetCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s bA of A in B);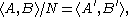 
where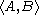 
is the subgroup of 
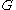generatedGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by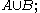
-
and -
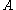is a normal subgroup of 
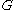if and only if 
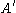is a normal subgroup of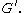 
This list is far from exhaustive. In fact, most properties of subgroups are preserved in their images under the bijection onto subgroups of a quotient group.