
Irreducible (mathematics)
Encyclopedia
In mathematics
, the concept of irreducibility is used in several ways.
The notions of irreducibility in algebra and manifold theory are related. An n-manifold is called prime
, if it cannot be written as a connected sum
of two n-manifolds (neither of which is an n-sphere). An irreducible manifold is thus prime, although the converse does not hold. From an algebraist's perspective, prime manifolds should be called "irreducible"; however, the topologist (in particular the 3-manifold
topologist) finds the definition above more useful. The only compact, connected 3-manifolds that are prime but not irreducible are the trivial 2-sphere bundle over S1 and the twisted 2-sphere bundle over S1. See, for example, Prime decomposition (3-manifold)
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the concept of irreducibility is used in several ways.
- In abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, irreducible can be an abbreviation for irreducible elementIrreducible elementIn abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
; for example an irreducible polynomialIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
.
- In representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, an irreducible representation is a nontrivial representationRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
with no nontrivial proper subrepresentations. Similarly, an irreducible module is another name for a simple moduleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
.
- Absolutely irreducibleAbsolutely irreducibleIn mathematics, absolutely irreducible is a term applied to linear representations or algebraic varieties over a field. It means that the object in question remains irreducible, even after any finite extension of the field of coefficients...
is a term applied to mean irreducible, even after any finite extension of the fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of coefficients. It applies in various situations, for example to irreducibility of a linear representation, or of an algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
; where it means just the same as irreducible over an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
.
- In commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R is irreducible if its prime spectrum, that is, the topological space Spec R, is an irreducible topological space.
- A directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
is irreducible if, given any two vertices, there exists a path from the first vertex to the second (see also connectivity in graphsConnectivity (graph theory)In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
). A digraph is irreducible if and only if its adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
is irreducible.
- In a related notion, a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is irreducible if it is not similar to a block upper triangular matrix with two blocks via a permutationPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
. (Replacing non-zero entries in the matrix by one, and viewing the matrix as an adjacency matrix of a graph, the matrix is irreducible if and only if the graph is irreducible.)
- Also, a Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
is irreducible if there is a non-zero probability of transitioning (even if in more than one step) from any state to any other state.
- In the theory of manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, an n-manifold is irreducible if any embedded (n − 1)-sphere bounds an embedded n-ball. Implicit in this definition is the use of a suitable categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, such as the category of differentiable manifolds or the category of piecewise-linear manifolds.
The notions of irreducibility in algebra and manifold theory are related. An n-manifold is called prime
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
, if it cannot be written as a connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of two n-manifolds (neither of which is an n-sphere). An irreducible manifold is thus prime, although the converse does not hold. From an algebraist's perspective, prime manifolds should be called "irreducible"; however, the topologist (in particular the 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
topologist) finds the definition above more useful. The only compact, connected 3-manifolds that are prime but not irreducible are the trivial 2-sphere bundle over S1 and the twisted 2-sphere bundle over S1. See, for example, Prime decomposition (3-manifold)
Prime decomposition (3-manifold)
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
.
- A topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is irreducible if it is not the union of two proper closed subsets. This notion is used in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, where spaces are equipped with the Zariski topologyZariski topologyIn algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
; it is not of much significance for Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s. See also irreducible componentIrreducible componentIn mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
, algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
- In universal algebraUniversal algebraUniversal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, irreducible can refer to the inability to represent an algebraic structureAlgebraic structureIn abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
as a composition of simpler structures using a product construction; for example subdirectly irreducible.
- A 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
is P²-irreducibleP²-irreducibleIn mathematics, a 3-manifold is P2-irreducible if it is irreducible and contains no 2-sided \mathbb RP^2 ....
if it is irreducibleIrreducible (mathematics)In mathematics, the concept of irreducibility is used in several ways.* In abstract algebra, irreducible can be an abbreviation for irreducible element; for example an irreducible polynomial....
and contains no 2-sided2-sidedIn topology, a compact codimension one submanifold F of a manifold M is said to be 2-sided in M when there is an embeddingwith h=x for each x\in F andIn other words, if its normal bundle is trivial....
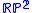 (real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
(real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
).
- An Irreducible fractionIrreducible fractionAn irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
(or fraction in lowest terms) is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent fraction.

