
Irreducible component
Encyclopedia
In mathematics
, the concept of irreducible component is used to make formal the idea that a set such as defined by the equation
is the union of the two lines
and
The notion of irreducibility is stronger than connectedness
.
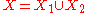 of two closed
of two closed
proper subsets
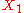 ,
, 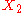 of
of  .
.
A topological space is irreducible (or hyperconnected
) if it is not reducible. Equivalently, all non empty open
subsets of X are dense
or any two nonempty open sets have nonempty intersection
.
A subset F of a topological space X is called irreducible or reducible, if F considered as a topological space via the subspace topology
has the corresponding property in the above sense. That is, is reducible if it can be written as a union
is reducible if it can be written as a union  where
where 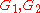 are closed subsets of
are closed subsets of  , neither of which contains
, neither of which contains  .
.
An irreducible component of a topological space
is a maximal
irreducible
subset. If a subset is irreducible, its closure
is, so irreducible components are closed
.
or scheme
X is the union of its irreducible components Xi. In most cases occurring in "practice", namely for all noetherian schemes, there are finitely many irreducible components. There is the following description of irreducible affine varieties or schemes X = Spec A: X is irreducible iff
the coordinate ring A of X has one minimal prime ideal
. This follows from the definition of the Zariski topology
. In particular, if A has no zero divisor
s, Spec A is irreducible, because then the zero-ideal is the minimal prime ideal.
As a matter of commutative algebra
, the primary decomposition of an ideal gives rise to the decomposition into irreducible components; and is somewhat finer in the information it gives, since it is not limited to radical ideals.
An affine variety or scheme X = Spec A is connected
iff A has no nontrivial (i.e. ≠0 or 1) idempotents. Geometrically, a nontrivial idempotent e corresponds to the function on X which is equal to 1 on some connected component(s) and 0 on others.
Irreducible components serve to define the dimension
of schemes.
However, the notion is fundamental and more meaningful in algebraic geometry
: consider the variety
(a subset of the affine plane, x and y are the variables) endowed with the Zariski topology
. It is reducible, its irreducible components are its closed subsets {x = 0} and {y = 0}.
This can also be read off the coordinate ring k[x, y]/(xy) (if the variety is defined over a field
k), whose minimal prime ideals are (x) and (y).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the concept of irreducible component is used to make formal the idea that a set such as defined by the equation
- XY = 0
is the union of the two lines
- X = 0
and
- Y = 0.
The notion of irreducibility is stronger than connectedness
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
.
Definition
A topological space X is reducible if it can be written as a union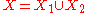 of two closed
of two closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
proper subsets
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
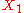 ,
, 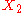 of
of  .
.A topological space is irreducible (or hyperconnected
Hyperconnected space
In mathematics, a hyperconnected space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry....
) if it is not reducible. Equivalently, all non empty open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subsets of X are dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
or any two nonempty open sets have nonempty intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
A subset F of a topological space X is called irreducible or reducible, if F considered as a topological space via the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
has the corresponding property in the above sense. That is,
 is reducible if it can be written as a union
is reducible if it can be written as a union  where
where 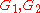 are closed subsets of
are closed subsets of  , neither of which contains
, neither of which contains  .
.An irreducible component of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a maximal
Maximal
Maximal may refer to:*Maximal element, a mathematical definition*Maximal , a faction of Transformers*Maximalism, an artistic style*Maximal set*Maxim , a men's magazine marketed as Maximal in several countriesSee also...
irreducible
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
subset. If a subset is irreducible, its closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
is, so irreducible components are closed
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
Use in algebraic geometry
In general algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
or scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X is the union of its irreducible components Xi. In most cases occurring in "practice", namely for all noetherian schemes, there are finitely many irreducible components. There is the following description of irreducible affine varieties or schemes X = Spec A: X is irreducible iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
the coordinate ring A of X has one minimal prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
. This follows from the definition of the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
. In particular, if A has no zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, Spec A is irreducible, because then the zero-ideal is the minimal prime ideal.
As a matter of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the primary decomposition of an ideal gives rise to the decomposition into irreducible components; and is somewhat finer in the information it gives, since it is not limited to radical ideals.
An affine variety or scheme X = Spec A is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
iff A has no nontrivial (i.e. ≠0 or 1) idempotents. Geometrically, a nontrivial idempotent e corresponds to the function on X which is equal to 1 on some connected component(s) and 0 on others.
Irreducible components serve to define the dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of schemes.
Examples
The irreducibility depends much on actual topology on some set. For example, possibly contradicting the intuition, the real numbers (with their usual topology) are reducible: for example the open interval (−1, 1) is not dense, its closure is the closed interval [−1, 1].However, the notion is fundamental and more meaningful in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
: consider the variety
- X := {x · y = 0}
(a subset of the affine plane, x and y are the variables) endowed with the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
. It is reducible, its irreducible components are its closed subsets {x = 0} and {y = 0}.
This can also be read off the coordinate ring k[x, y]/(xy) (if the variety is defined over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k), whose minimal prime ideals are (x) and (y).

