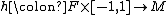2-sided
Encyclopedia
In topology
, a compact codimension
one submanifold
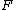 of a manifold
of a manifold
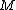 is said to be 2-sided in
is said to be 2-sided in 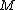 when there is an embedding
when there is an embedding
with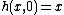 for each
for each 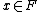 and
and
In other words, if its normal bundle
is trivial.
This means, for example that a curve in a surface is 2-sided if it has a tubular neighborhood
which is a cartesian product of the curve times an interval.
A submanifold which is not 2-sided is called 1-sided.
. This can be determined from the class of the curve in the fundamental group
of the surface and the orientation character on the fundamental group, which identifies which curves reverse orientation.
has been done – but need not, such as cutting along a curve on the torus
.
Cutting along a (connected) 1-sided manifold does not separate a manifold, as a point that is locally on one side of the manifold can be connected to a point that is locally on the other side (i.e., just across the submanifold) by passing along an orientation-reversing path.
Cutting along a 1-sided manifold may make a non-orientable manifold orientable – such as cutting along an equator of the real projective plane – but may not, such as cutting along a 1-sided curve in a higher genus non-orientable surface,
maybe the simplest example of this is seen when one cut a mobius band
along its core curve.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a compact codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
one submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
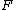 of a manifold
of a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
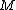 is said to be 2-sided in
is said to be 2-sided in 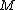 when there is an embedding
when there is an embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
with
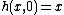 for each
for each 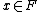 and
and
-
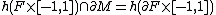 .
.
In other words, if its normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
is trivial.
This means, for example that a curve in a surface is 2-sided if it has a tubular neighborhood
Tubular neighborhood
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
which is a cartesian product of the curve times an interval.
A submanifold which is not 2-sided is called 1-sided.
Surfaces
For curves on surfaces, a curve is 2-sided if and only if it preserves orientation, and 1-sided if and only if it reverses orientation: a tubular neighborhood is then a Möbius stripMöbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. This can be determined from the class of the curve in the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the surface and the orientation character on the fundamental group, which identifies which curves reverse orientation.
- An embedded circle in the plane is 2-sided.
- An embedded circle generating the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
(such as an "equator" of the projective plane – the image of an equator for the sphere) is 1-sided, as it is orientation-reversing.
Properties
Cutting along a 2-sided manifold can separate a manifold into two pieces – such as cutting along the equator of a sphere or around the sphere on which a connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
has been done – but need not, such as cutting along a curve on the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
.
Cutting along a (connected) 1-sided manifold does not separate a manifold, as a point that is locally on one side of the manifold can be connected to a point that is locally on the other side (i.e., just across the submanifold) by passing along an orientation-reversing path.
Cutting along a 1-sided manifold may make a non-orientable manifold orientable – such as cutting along an equator of the real projective plane – but may not, such as cutting along a 1-sided curve in a higher genus non-orientable surface,
maybe the simplest example of this is seen when one cut a mobius band
Mobius Band
Mobius Band is an electronic rock trio from Brooklyn, New York consisting of Noam Schatz , Peter Sax , and Ben Sterling .-History:...
along its core curve.