Inverse function theorem
Encyclopedia
In mathematics
, specifically differential calculus
, the inverse function theorem gives sufficient conditions for a function
to be invertible in a neighborhood
of a point in its domain
. The theorem also gives a formula
for the derivative
of the inverse function
.
In multivariable calculus
, this theorem can be generalized to any vector-valued function
whose Jacobian determinant
is nonzero at a point in its domain. In this case, the theorem gives a formula for the Jacobian matrix
of the inverse. There are also versions of the inverse function theorem for complex holomorphic function
s, for differentiable maps between manifold
s, for differentiable functions between Banach space
s, and so forth.
, the theorem states that if ƒ is a continuously differentiable function with nonzero derivative at the point a, then ƒ is invertible in a neighborhood of a, the inverse is continuously differentiable, and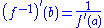
where b = ƒ(a).
For functions of more than one variable, the theorem states that if the total derivative of a continuously differentiable function F defined from an open set U of Rn into Rn is invertible at a point p (i.e., the Jacobian determinant of F at p is non-zero), then F is an invertible function near p. That is, an inverse function
to F exists in some neighborhood
of F(p). Moreover, the inverse function
is also continuously differentiable. In the infinite dimensional case it is required that the Fréchet derivative
have a bounded inverse at p.
Finally, the theorem says that
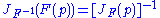
where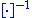
denotes matrix inverse and 
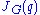is the Jacobian matrix of the function G at
the point q.
This formula can also be derived from the chain rule
. The chain rule states that for functions G and H which have total derivatives at H(p) and p respectively,
Letting G be F -1 and H be F,
is the identity function, whose Jacobian matrix is also
the identity. In this special case, the formula above can be solved for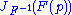
.
Note that the chain rule assumes the existence of total derivative of the inside function H, while
the inverse function theorem proves that F-1 has a total derivative at p.
The existence of an inverse function to F is equivalent to saying that the system of n equations yi = Fj(x1,...,xn) can be solved for x1,...,xn in terms of y1,...,yn if we restrict x and y to small enough neighborhoods of p and F(p), respectively.
F from R2 to R2 defined by
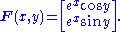
Then the Jacobian matrix is
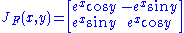
and the determinant is
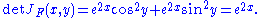
The determinant e2x is nonzero everywhere. By the theorem, for every point p in R2, there exists a neighborhood about p over which F is invertible. Note that this is different than saying F is invertible over its entire image. In this example, F is not invertible because it is not injective (because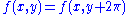
.)
s. In this context the theorem states that for a differentiable map F : M → N, if the derivative of F,
p : TpM → TF(p)N
is a linear isomorphism at a point p in M then there exists an open neighborhood U of p such that
is a diffeomorphism
. Note that this implies that M and N must have the same dimension at p.
If the derivative of F is an isomorphism at all points p in M then the map F is a local diffeomorphism
.
s. Let X and Y be Banach spaces and U an open neighbourhood of the origin in X. Let F : U → Y be continuously differentiable and assume that the derivative (dF)0 : X → Y of F at 0 is a bounded linear isomorphism of X onto Y. Then there exists an open neighbourhood V of F(0) in Y and a continuously differentiable map G : V → X such that F(G(y)) = y for all y in V. Moreover, G(y) is the only sufficiently small solution x of the equation F(x) = y.
s.
) can be seen as a special case of the constant rank theorem, which states that a smooth map with locally constant rank near a point can be put in a particular normal form near that point. When the derivative of F is invertible at a point p, it is also invertible in a neighborhood of p, and hence the rank of the derivative is constant, so the constant rank theorem applies.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, the inverse function theorem gives sufficient conditions for a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
to be invertible in a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of a point in its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
. The theorem also gives a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
for the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
.
In multivariable calculus
Multivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
, this theorem can be generalized to any vector-valued function
Vector-valued function
A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
whose Jacobian determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is nonzero at a point in its domain. In this case, the theorem gives a formula for the Jacobian matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of the inverse. There are also versions of the inverse function theorem for complex holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s, for differentiable maps between manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, for differentiable functions between Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, and so forth.
Statement of the theorem
For functions of a single variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, the theorem states that if ƒ is a continuously differentiable function with nonzero derivative at the point a, then ƒ is invertible in a neighborhood of a, the inverse is continuously differentiable, and
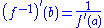
where b = ƒ(a).
For functions of more than one variable, the theorem states that if the total derivative of a continuously differentiable function F defined from an open set U of Rn into Rn is invertible at a point p (i.e., the Jacobian determinant of F at p is non-zero), then F is an invertible function near p. That is, an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
to F exists in some neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of F(p). Moreover, the inverse function
is also continuously differentiable. In the infinite dimensional case it is required that the Fréchet derivativeFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
have a bounded inverse at p.
Finally, the theorem says that
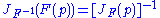
where
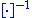denotes matrix inverse and 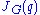is the Jacobian matrix of the function G atthe point q.
This formula can also be derived from the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. The chain rule states that for functions G and H which have total derivatives at H(p) and p respectively,
Letting G be F -1 and H be F,
is the identity function, whose Jacobian matrix is alsothe identity. In this special case, the formula above can be solved for
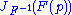.Note that the chain rule assumes the existence of total derivative of the inside function H, while
the inverse function theorem proves that F-1 has a total derivative at p.
The existence of an inverse function to F is equivalent to saying that the system of n equations yi = Fj(x1,...,xn) can be solved for x1,...,xn in terms of y1,...,yn if we restrict x and y to small enough neighborhoods of p and F(p), respectively.
Example
Consider the vector-valued functionVector-valued function
A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
F from R2 to R2 defined by
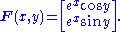
Then the Jacobian matrix is
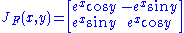
and the determinant is
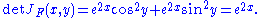
The determinant e2x is nonzero everywhere. By the theorem, for every point p in R2, there exists a neighborhood about p over which F is invertible. Note that this is different than saying F is invertible over its entire image. In this example, F is not invertible because it is not injective (because
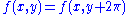.)Manifolds
The inverse function theorem can be generalized to differentiable maps between differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s. In this context the theorem states that for a differentiable map F : M → N, if the derivative of F,
p : TpM → TF(p)N
is a linear isomorphism at a point p in M then there exists an open neighborhood U of p such that
- F|U : U → F(U)
is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. Note that this implies that M and N must have the same dimension at p.
If the derivative of F is an isomorphism at all points p in M then the map F is a local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
.
Banach spaces
The inverse function theorem can also be generalized to differentiable maps between Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. Let X and Y be Banach spaces and U an open neighbourhood of the origin in X. Let F : U → Y be continuously differentiable and assume that the derivative (dF)0 : X → Y of F at 0 is a bounded linear isomorphism of X onto Y. Then there exists an open neighbourhood V of F(0) in Y and a continuously differentiable map G : V → X such that F(G(y)) = y for all y in V. Moreover, G(y) is the only sufficiently small solution x of the equation F(x) = y.
Banach manifolds
These two directions of generalization can be combined in the inverse function theorem for Banach manifoldBanach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
s.
Constant rank theorem
The inverse function theorem (and the implicit function theoremImplicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
) can be seen as a special case of the constant rank theorem, which states that a smooth map with locally constant rank near a point can be put in a particular normal form near that point. When the derivative of F is invertible at a point p, it is also invertible in a neighborhood of p, and hence the rank of the derivative is constant, so the constant rank theorem applies.