Neighbourhood (mathematics)
Encyclopedia
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
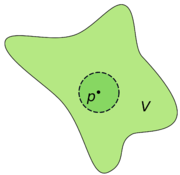
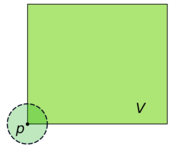
, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
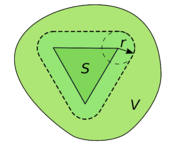
. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.
This concept is closely related to the concepts of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
Definition
If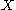
is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and
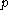is a point in 
, a neighbourhood of 
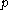is a set 
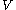, which includes an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
containing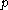 
,
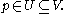
This is also equivalent to
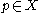being in the interior of 
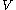.Note that the neighbourhood
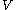need not be an open set itself. If 
is open it is called an open neighbourhood. Some authors require that neighbourhoods be open, so it is important to note conventions.A set which is a neighbourhood of each of its points is open since it can be expressed as the union of open sets containing each of its points.
The collection of all neighbourhoods of a point is called the neighbourhood system at the point.
If
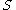is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
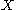then a neighbourhood of 
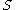is a set 
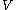which includes an open set 
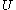containing 
. It follows that a set 
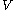is a neighbourhood of 
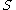if and only if it is a neighbourhood of all the points in 
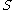. Furthermore, it follows that 
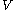is a neighbourhood of 
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
is a subset of the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of
.In a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
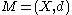, a set 
is a neighbourhood of a point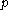 
if there exists an open ball with centre 
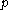and radius 
, such that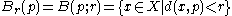
is contained in
.
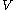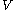is called uniform neighbourhood of a set 
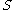if there exists a positive number 
such that for all elements 
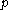of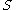 
,
is contained in
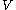.For
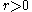the 
-neighbourhood 
of a set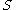 
is the set of all points in 
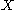which are at distance less than 
from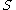 
(or equivalently,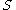 
is the union of all the open balls of radius 
which are centred at a point in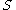 
).It directly follows that an
-neighbourhood is a uniform neighbourhood, and that a set is a uniform neighbourhood if and only if it contains an 
-neighbourhood for some value of 
.Examples
Given the set of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
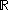with the usual Euclidean metric and a subset 
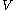defined as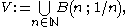
then
is a neighbourhood for the set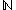 
of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, but is not a uniform neighbourhood of this set.
Topology from neighbourhoods
The above definition is useful if the notion of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
is already defined. There is an alternative way to define a topology, by first defining the neighbourhood system, and then open sets as those sets containing a neighbourhood of each of their points.
A neighbourhood system on
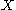is the assignment of a filterFilter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
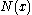(on the set 
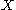) to each 
in 
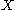, such that
- the point
is an element of each 
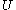in 
- each
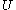in 
contains some 
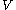in 
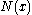such that for each 
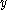in 
, 
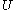is in 
.
One can show that both definitions are compatible, i.e. the topology obtained from the neighbourhood system defined using open sets is the original one, and vice versa when starting out from a neighbourhood system.
Uniform neighbourhoods
In a uniform spaceUniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
, 
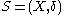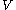is called a uniform neighbourhood of 
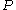if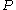 
is not closeCloseness (mathematics)
In topology and related areas in mathematics closeness is one of the basic concepts in a topological space. Intuitively we say two sets are close if they are arbitrarily near to each other...
to
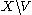, that is there exists no entourage containing 
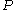and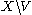 
.Punctured neighbourhood
A punctured neighbourhood of a point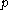
(sometimes called a deleted neighbourhood) is a neighbourhood of 
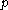, without 
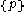. For instance, the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
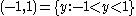is a neighbourhood of 
in the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, so the set
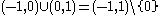is a punctured neighbourhood of 
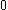. Note that a punctured neighbourhood of a given point is not in fact a neighbourhood of the point. The concept of punctured neighbourhood occurs in the definition of the limit of a function.