Glossary of graph theory
Encyclopedia
Graph theory
is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage.
G consists of two types of elements, namely vertices
and edges. Every edge has two endpoints in the set of vertices, and is said to connect or join the two endpoints. An edge can thus be defined as a set of two vertices (or an ordered pair, in the case of a directed graph - see Section Direction).
Alternative models of graphs exist; e.g., a graph may be thought of as a Boolean binary function
over the set of vertices or as a square (0,1)-matrix
.
A vertex is simply drawn as a node or a dot. The vertex set of G is usually denoted by V(G), or V when there is no danger of confusion. The order of a graph is the number of its vertices, i.e. |V(G)|.
An edge (a set of two elements) is drawn as a line connecting two vertices, called endpoints or (less often) endvertices. An edge with endvertices x and y is denoted by xy (without any symbol in between). The edge set of G is usually denoted by E(G), or E when there is no danger of confusion.
The size of a graph is the number of its edges, i.e. |E(G)|.
A loop
is an edge whose endpoints are the same vertex. A link has two distinct endvertices. An edge is multiple if there is another edge with the same endvertices; otherwise it is simple. The multiplicity of an edge is the number of multiple edges sharing the same end vertices; the multiplicity of a graph, the maximum multiplicity of its edges. A graph is a simple graph if it has no multiple edges or loops, a multigraph if it has multiple edges, but no loops, and a multigraph or pseudograph if it contains both multiple edges and loops (the literature is highly inconsistent). When stated without any qualification, a graph is almost always assumed to be simple—one has to judge from the context.
Graphs whose edges or vertices have names or labels are known as labeled, those without as unlabeled. Graphs with labeled vertices only are vertex-labeled, those with labeled edges only are edge-labeled. The difference between a labeled and an unlabeled graph is that the latter has no specific set of vertices or edges; it is regarded as another way to look upon an isomorphism type of graphs. (Thus, this usage distinguishes between graphs with identifiable vertex or edge sets on the one hand, and isomorphism types or classes of graphs on the other.)
(Graph labeling
usually refers to the assignment of labels (usually natural numbers, usually distinct) to the edges and vertices of a graph, subject to certain rules depending on the situation. This should not be confused with a graph's merely having distinct labels or names on the vertices.)
 A hyperedge is an edge that is allowed to take on any number of vertices, possibly more than 2. A graph that allows any hyperedge is called a hypergraph
A hyperedge is an edge that is allowed to take on any number of vertices, possibly more than 2. A graph that allows any hyperedge is called a hypergraph
. A simple graph can be considered a special case of the hypergraph, namely the 2-uniform hypergraph. However, when stated without any qualification, an edge is always assumed to consist of at most 2 vertices, and a graph is never confused with a hypergraph.
A non-edge (or anti-edge) is an edge that is not present in the graph. More formally, for two vertices and
and  ,
,  is a non-edge in a graph
is a non-edge in a graph  whenever
whenever  is not an edge in
is not an edge in  . This means that there is either no edge between the two vertices or (for directed graphs) at most one of
. This means that there is either no edge between the two vertices or (for directed graphs) at most one of  and
and  from
from  is an arc in G.
is an arc in G.
Occasionally the term cotriangle or anti-triangle is used for a set of three vertices none of which are connected.
The complement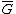 of a graph G is a graph with the same vertex set as G but with an edge set such that xy is an edge in
of a graph G is a graph with the same vertex set as G but with an edge set such that xy is an edge in 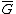 if and only if xy is not an edge in G.
if and only if xy is not an edge in G.
An edgeless graph or empty graph or null graph is a graph with zero or more vertices, but no edges. The empty graph or null graph may also be the graph with no vertices and no edges. If it is a graph with no edges and any number of vertices, it may be called the null graph on
of vertices, it may be called the null graph on  vertices. (There is no consistency at all in the literature.)
vertices. (There is no consistency at all in the literature.)
A graph is infinite if it has infinitely many vertices or edges or both; otherwise the graph is finite. An infinite graph where every vertex has finite degree is called locally finite. When stated without any qualification, a graph is usually assumed to be finite. See also continuous graph.
Two graphs G and H are said to be isomorphic, denoted by G ~ H, if there is a one-to-one correspondence, called an isomorphism, between the vertices of the graph such that two vertices are adjacent in G if and only if their corresponding vertices are adjacent in H. Likewise, a graph G is said to be homomorphic to a graph H if there is a mapping, called a homomorphism
, from V(G) to V(H) such that if two vertices are adjacent in G then their corresponding vertices are adjacent in H.
A subgraph H is a spanning subgraph, or factor, of a graph G if it has the same vertex set as G. We say H spans G.
A subgraph H of a graph G is said to be induced if, for any pair of vertices x and y of H, xy is an edge of H if and only if xy is an edge of G. In other words, H is an induced subgraph of G if it has exactly the edges that appear in G over the same vertex set. If the vertex set of H is the subset S of V(G), then H can be written as G[S] and is said to be induced by S.
A graph that does not contain H as an induced subgraph is said to be H-free.
A universal graph in a class K of graphs is a simple graph in which every element in K can be embedded as a subgraph.
A graph G is minimal with some property P provided that G has property P and no proper subgraph of G has property P. In this definition, the term subgraph is usually understood to mean "induced subgraph." The notion of maximality is defined dually
: G is maximal with P provided that P(G) and G has no supergraph H such that P(H).
Many important classes of graphs can be defined by sets of forbidden subgraphs, the minimal graphs that are not in the class.
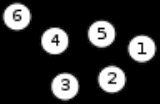
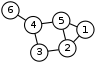
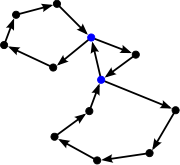
The length l of a walk is the number of edges that it uses. For an open walk, l = n–1, where n is the number of vertices visited (a vertex is counted each time it is visited). For a closed walk, l = n (the start/end vertex is listed twice, but is not counted twice). In the example graph, (1, 2, 5, 1, 2, 3) is an open walk with length 5, and (4, 5, 2, 1, 5, 4) is a closed walk of length 5.
A trail is a walk in which all the edges are distinct. A closed trail has been called a tour or circuit, but these are not universal, and the latter is often reserved for a regular subgraph of degree two.
 Traditionally, a path
Traditionally, a path
referred to what is now usually known as an open walk. Nowadays, when stated without any qualification, a path is usually understood to be simple, meaning that no vertices (and thus no edges) are repeated. (The term chain has also been used to refer to a walk in which all vertices and edges are distinct.) In the example graph, (5, 2, 1) is a path of length 2. The closed equivalent to this type of walk, a walk that starts and ends at the same vertex but otherwise has no repeated vertices or edges, is called a cycle
. Like path, this term traditionally referred to any closed walk, but now is usually understood to be simple by definition. In the example graph, (1, 5, 2, 1) is a cycle of length 3. (A cycle, unlike a path, is not allowed to have length 0.) Paths and cycles of n vertices are often denoted by Pn and Cn, respectively. (Some authors use the length instead of the number of vertices, however.)
C1 is a loop, C2 is a digon (a pair of parallel undirected edges in a multigraph
, or a pair of antiparallel edges in a directed graph), and C3 is called a triangle.
A cycle that has odd length is an odd cycle; otherwise it is an even cycle. One theorem is that a graph is bipartite
if and only if it contains no odd cycles. (See complete bipartite graph
.)
A graph is acyclic if it contains no cycles; unicyclic if it contains exactly one cycle; and pancyclic
if it contains cycles of every possible length (from 3 to the order of the graph).
The girth of a graph is the length of a shortest (simple) cycle in the graph; and the circumference, the length of a longest (simple) cycle. The girth and circumference of an acyclic graph are defined to be infinity
∞.
A path or cycle is Hamiltonian
(or spanning) if it uses all vertices exactly once. A graph that contains a Hamiltonian path is traceable; and one that contains a Hamiltonian path for any given pair of (distinct) end vertices is a Hamiltonian connected graph. A graph that contains a Hamiltonian cycle is a Hamiltonian graph.
A trail or circuit (or cycle) is Eulerian
if it uses all edges precisely once. A graph that contains an Eulerian trail is traversable. A graph that contains an Eulerian circuit is an Eulerian graph.
Two paths are internally disjoint (some people call it independent) if they do not have any vertex in common, except the first and last ones.
A theta graph is the union of three internally disjoint (simple) paths that have the same two distinct end vertices. A theta0 graph has seven vertices which can be arranged as the vertices of a regular hexagon plus an additional vertex in the center. The eight edges are the perimeter of the hexagon plus one diameter.
 A tree
A tree
is a connected acyclic simple graph. For directed graphs, each vertex has at most one incoming edge. A vertex of degree 1 is called a leaf, or pendant vertex. An edge incident to a leaf is a leaf edge, or pendant edge. (Some people define a leaf edge as a leaf and then define a leaf vertex on top of it. These two sets of definitions are often used interchangeably.) A non-leaf vertex is an internal vertex. Sometimes, one vertex of the tree is distinguished, and called the root; in this case, the tree is called rooted. Rooted trees are often treated as directed acyclic graph
s with the edges pointing away from the root.
A subtree of the tree T is a connected subgraph of T.
A forest is an acyclic simple graph. For directed graphs, each vertex has at most one incoming edge. (That is, a tree with the connectivity requirement removed; a graph containing multiple disconnected trees.)
A subforest of the forest F is a subgraph of F.
A spanning tree
is a spanning subgraph that is a tree. Every graph has a spanning forest. But only a connected graph has a spanning tree.
A special kind of tree called a star
is K1,k. An induced star with 3 edges is a claw.
A caterpillar
is a tree in which all non-leaf nodes form a single path.
A k-ary tree is a rooted tree in which every internal vertex has k children. A 1-ary tree is just a path. A 2-ary tree is also called a binary tree.
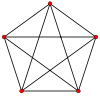 The complete graph
The complete graph
Kn of order n is a simple graph with n vertices in which every vertex is adjacent to every other. The example graph to the right is complete. The complete graph on n vertices is often denoted by Kn. It has n(n-1)/2 edges (corresponding to all possible choices of pairs of vertices).
A clique
in a graph is a set of pairwise adjacent vertices. Since any subgraph induced by a clique is a complete subgraph, the two terms and their notations are usually used interchangeably. A k-clique is a clique of order k. In the example graph above, vertices 1, 2 and 5 form a 3-clique, or a triangle. A maximal clique is a clique that is not a subset of any other clique (some authors reserve the term clique for maximal cliques).
The clique number ω(G) of a graph G is the order of a largest clique in G.
. Informally, a strongly connected component of a directed graph is a subgraph where all nodes in the subgraph are reachable by all other nodes in the subgraph. Reachability between nodes is established by the existence of a path between the nodes.
A directed graph can be decomposed into strongly connected components by running the depth-first search
(DFS) algorithm twice: first, on the graph itself and next on the transpose
of the graph in decreasing order of the finishing times of the first DFS. Given a directed graph G, the transpose GT is the graph G with all the edge directions reversed.
 of
of 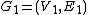 is an injection
is an injection
from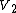 to
to 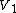 such that every edge in
such that every edge in 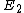 corresponds to a path (disjoint from all other such paths) in
corresponds to a path (disjoint from all other such paths) in 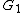 such that every vertex in
such that every vertex in  is in one or more paths, or is part of the injection from
is in one or more paths, or is part of the injection from 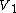 to
to  . This can alternatively be phrased in terms of contractions, which are operations which collapse a path and all vertices on it into a single edge (see Minor (graph theory)
. This can alternatively be phrased in terms of contractions, which are operations which collapse a path and all vertices on it into a single edge (see Minor (graph theory)
).
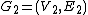 of
of  is an injection
is an injection
from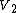 to
to 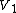 such that every edge in
such that every edge in  corresponds to a path (disjoint from all other such paths) in
corresponds to a path (disjoint from all other such paths) in 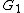 .
.
An edge connects two vertices; these two vertices are said to be incident to that edge, or, equivalently, that edge incident to those two vertices. All degree-related concepts have to do with adjacency or incidence.
The degree
, or valency, dG(v) of a vertex v in a graph G is the number of edges incident to v, with loops being counted twice. A vertex of degree 0 is an isolated vertex. A vertex of degree 1 is a leaf. In the labelled simple graph example, vertices 1 and 3 have a degree of 2, vertices 2, 4 and 5 have a degree of 3, and vertex 6 has a degree of 1. If E is finite, then the total sum of vertex degrees is equal to twice the number of edges.
The total degree of a graph is equal to two times the number of edges, loops included. This means that for a graph with 3 vertices with each vertex having a degree of two (i.e. a triangle) the total degree would be six (e.g. 3 x 2 = 6). The general formula for this is total degree = 2n where n = number of edges.
A degree sequence is a list of degrees of a graph in non-increasing order (e.g. d1 ≥ d2 ≥ … ≥ dn). A sequence of non-increasing integers is realizable if it is a degree sequence of some graph.
Two vertices u and v are called adjacent if an edge exists between them. We denote this by u ~ v or u ↓ v. In the above graph, vertices 1 and 2 are adjacent, but vertices 2 and 4 are not. The set of neighbors of v, that is, vertices adjacent to v not including v itself, forms an induced subgraph called the (open) neighborhood
of v and denoted NG(v). When v is also included, it is called a closed neighborhood and denoted by NG[v]. When stated without any qualification, a neighborhood is assumed to be open. The subscript G is usually dropped when there is no danger of confusion; the same neighborhood notation may also be used to refer to sets of adjacent vertices rather than the corresponding induced subgraphs. In the example graph, vertex 1 has two neighbors: vertices 2 and 5. For a simple graph, the number of neighbors that a vertex has coincides with its degree.
A dominating set of a graph is a vertex subset whose closed neighborhood includes all vertices of the graph. A vertex v dominates another vertex u if there is an edge from v to u. A vertex subset V dominates another vertex subset U if every vertex in U is adjacent to some vertex in V. The minimum size of a dominating set is the domination number γ(G).
In computers, a finite, directed or undirected graph (with n vertices, say) is often represented by its adjacency matrix
: an n-by-n matrix
whose entry in row i and column j gives the number of edges from the i-th to the j-th vertex.
Spectral graph theory
studies relationships between the properties of the graph and its adjacency matrix.
The maximum degree Δ(G) of a graph G is the largest degree over all vertices; the minimum degree δ(G), the smallest.
A graph in which every vertex has the same degree is regular
. It is k-regular if every vertex has degree k. A 0-regular graph is an independent set. A 1-regular graph is a matching. A 2-regular graph is a vertex disjoint union of cycles. A 3-regular graph is said to be cubic, or trivalent.
A k-factor is a k-regular spanning subgraph. A 1-factor is a perfect matching. A partition of edges of a graph into k-factors is called a k-factorization. A k-factorable graph is a graph that admits a k-factorization.
A graph is biregular if it has unequal maximum and minimum degrees and every vertex has one of those two degrees.
A strongly regular graph is a regular graph such that any adjacent vertices have the same number of common neighbors as other adjacent pairs and that any nonadjacent vertices have the same number of common neighbors as other nonadjacent pairs.
, or coclique, or stable set or staset, is a set of vertices of which no pair is adjacent. Since the graph induced by any independent set is an empty graph, the two terms are usually used interchangeably. In the example above, vertices 1, 3, and 6 form an independent set; and 3, 5, and 6 form another one.
Two subgraphs are edge disjoint if they have no edges in common. Similarly, two subgraphs are vertex disjoint if they have no vertices (and thus, also no edges) in common. Unless specified otherwise, a set of disjoint subgraphs are assumed to be pairwise vertex disjoint.
The independence number α(G) of a graph G is the size of the largest independent set of G.
A graph can be decomposed into independent sets in the sense that the entire vertex set of the graph can be partitioned into pairwise disjoint independent subsets. Such independent subsets are called partite sets, or simply parts.
A graph that can be decomposed into two partite sets but not fewer is bipartite
; three sets but not fewer, tripartite; k sets but not fewer, k-partite; and an unknown number of sets, multipartite. An 1-partite graph is the same as an independent set, or an empty graph. A 2-partite graph is the same as a bipartite graph. A graph that can be decomposed into k partite sets is also said to be k-colourable.
A complete multipartite graph is a graph in which vertices are adjacent if and only if they belong to different partite sets. A complete bipartite graph
is also referred to as a biclique; if its partite sets contain n and m vertices, respectively, then the graph is denoted Kn,m.
A k-partite graph is semiregular if each of its partite sets has a uniform degree; equipartite if each partite set has the same size; and balanced k-partite if each partite set differs in size by at most 1 with any other.
The matching number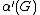 of a graph G is the size of a largest matching, or pairwise vertex disjoint edges, of G.
of a graph G is the size of a largest matching, or pairwise vertex disjoint edges, of G.
A spanning matching, also called a perfect matching is a matching that covers all vertices of a graph.
extends the concept of adjacency and is essentially a form (and measure) of concatenated adjacency.
If it is possible to establish a path from any vertex to any other vertex of a graph, the graph is said to be connected; otherwise, the graph is disconnected. A graph is totally disconnected if there is no path connecting any pair of vertices. This is just another name to describe an empty graph or independent set.
A cut vertex, or articulation point, is a vertex whose removal disconnects the remaining subgraph. A cut set, or vertex cut or separating set, is a set of vertices whose removal disconnects the remaining subgraph. A bridge is an analogous edge (see below).
If it is always possible to establish a path from any vertex to every other even after removing any k - 1 vertices, then the graph is said to be k-vertex-connected
or k-connected. Note that a graph is k-connected if and only if it contains k internally disjoint paths between any two vertices. The example graph above is connected (and therefore 1-connected), but not 2-connected. The vertex connectivity or connectivity κ(G) of a graph G is the minimum number of vertices that need to be removed to disconnect G. The complete graph Kn has connectivity n - 1 for n > 1; and a disconnected graph has connectivity 0.
In network theory
, a giant component
is a connected subgraph that contains a majority of the entire graph's nodes
.
A bridge
, or cut edge or isthmus, is an edge whose removal disconnects a graph. (For example, all the edges in a tree are bridges.) A disconnecting set is a set of edges whose removal increases the number of components. An edge cut is the set of all edges which have one vertex in some proper vertex subset S and the other vertex in V(G)\S. Edges of K3 form a disconnecting set but not an edge cut. Any two edges of K3 form a minimal
disconnecting set as well as an edge cut. An edge cut is necessarily a disconnecting set; and a minimal disconnecting set of a nonempty graph is necessarily an edge cut. A bond is a minimal (but not necessarily minimum), nonempty set of edges whose removal disconnects a graph. A cut vertex is an analogous vertex (see above).
A graph is k-edge-connected
if any subgraph formed by removing any k - 1 edges is still connected. The edge connectivity κ'(G) of a graph G is the minimum number of edges needed to disconnect G. One well-known result is that κ(G) ≤ κ'(G) ≤ δ(G).
A component is a maximally connected subgraph. A block is either a maximally 2-connected subgraph, a bridge (together with its vertices), or an isolated vertex. A biconnected component
is a 2-connected component.
An articulation point (also known as a separating vertex) of a graph is a vertex whose removal from the graph increases its number of connected components. A biconnected component can be defined as a subgraph induced by a maximal set of nodes that has no separating vertex.
dG(u, v) between two (not necessary distinct) vertices u and v in a graph G is the length of a shortest path between them. The subscript G is usually dropped when there is no danger of confusion. When u and v are identical, their distance is 0. When u and v are unreachable from each other, their distance is defined to be infinity
∞.
The eccentricity εG(v) of a vertex v in a graph G is the maximum distance from v to any other vertex. The diameter diam(G) of a graph G is the maximum eccentricity over all vertices in a graph; and the radius rad(G), the minimum. When there are two components in G, diam(G) and rad(G) defined to be infinity ∞. Trivially, diam(G) ≤ 2 rad(G). Vertices with maximum eccentricity are called peripheral vertices. Vertices of minimum eccentricity form the center. A tree has at most two center vertices.
The Wiener index of a vertex v in a graph G, denoted by WG(v) is the sum of distances between v and all others. The Wiener index of a graph G, denoted by W(G), is the sum of distances over all pairs of vertices. An undirected graph's Wiener polynomial is defined to be Σ qd(u,v) over all unordered pairs of vertices u and v. Wiener index and Wiener polynomial are of particular interest to mathematical chemists.
The k-th power Gk of a graph G is a supergraph formed by adding an edge between all pairs of vertices of G with distance at most k. A second power of a graph is also called a square.
A k-spanner is a spanning subgraph, S, in which every two vertices are at most k times as far apart on S than on G. The number k is the dilation. k-spanner is used for studying geometric network optimization.
of any surface on which the graph can embed.
A planar graph
is one which can be drawn on the (Euclidean) plane without any crossing; and a plane graph, one which is drawn in such fashion. In other words, a planar graph is a graph of genus 0. The example graph is planar; the complete graph on n vertices, for n> 4, is not planar. Also, a tree is necessarily a planar graph.
When a graph is drawn without any crossing, any cycle that surrounds a region without any edges reaching from the cycle into the region forms a face. Two faces on a plane graph are adjacent if they share a common edge. A dual, or planar dual when the context needs to be clarified, G* of a plane graph G is a graph whose vertices represent the faces, including any outerface, of G and are adjacent in G* if and only if their corresponding faces are adjacent in G. The dual of a planar graph is always a planar pseudograph (e.g. consider the dual of a triangle). In the familiar case of a 3-connected simple planar graph G (isomorphic to a convex polyhedron
P), the dual G* is also a 3-connected simple planar graph (and isomorphic to the dual polyhedron P*).
Furthermore, since we can establish a sense of "inside" and "outside" on a plane, we can identify an "outermost" region that contains the entire graph if the graph does not cover the entire plane. Such outermost region is called an outer face. An outerplanar graph
is one which can be drawn in the planar fashion such that its vertices are all adjacent to the outer face; and an outerplane graph, one which is drawn in such fashion.
The minimum number of crossings that must appear when a graph is drawn on a plane is called the crossing number
.
The minimum number of planar graphs needed to cover a graph is the thickness of the graph.
s. They may be restricted to rational numbers or integers. Certain algorithms require further restrictions on weights; for instance, Dijkstra's algorithm
works properly only for positive weights. The weight of a path or the weight of a tree in a weighted graph is the sum of the weights of the selected edges. Sometimes a non-edge is labeled by a special weight representing infinity. Sometimes the word cost is used instead of weight. When stated without any qualification, a graph is always assumed to be unweighted. In some writing on graph theory
the term network is a synonym for a weighted graph. A network may be directed or undirected, it may contain special vertices (nodes), such as source or sink. The classical network problems include:
A digraph is called simple if it has no loops and at most one arc between any pair of vertices. When stated without any qualification, a digraph is usually assumed to be simple.
In a digraph Γ, we distinguish the out degree dΓ+(v), the number of edges leaving a vertex v, and the in degree dΓ-(v), the number of edges entering a vertex v. If the graph is oriented, the degree dΓ(v) of a vertex v is equal to the sum of its out- and in- degrees. When the context is clear, the subscript Γ can be dropped. Maximum and minimum out degrees are denoted by Δ+(Γ) and δ+(Γ); and maximum and minimum in degrees, Δ-(Γ) and δ-(Γ).
An out-neighborhood, or successor set, N+Γ(v) of a vertex v is the set of heads of arcs going from v. Likewise, an in-neighborhood, or predecessor set, N-Γ(v) of a vertex v is the set of tails of arcs going into v.
A source is a vertex with 0 in-degree; and a sink, 0 out-degree.
A vertex v dominates another vertex u if there is an arc from v to u. A vertex subset S is out-dominating if every vertex not in S is dominated by some vertex in S; and in-dominating if every vertex in S is dominated by some vertex not in S.
A kernel is an independent out-dominating set. A digraph is kernel perfect if every induced sub-digraph has a kernel.
An Eulerian digraph is a digraph with equal in- and out-degrees at every vertex.
The zweieck of an undirected edge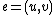 is the pair of diedges
is the pair of diedges
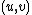 and
and 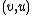 which form the simple dicircuit.
which form the simple dicircuit.
An orientation is an assignment of directions to the edges of an undirected or partially directed graph. When stated without any qualification, it is usually assumed that all undirected edges are replaced by a directed one in an orientation. Also, the underlying graph is usually assumed to be undirected and simple.
A tournament
is a digraph in which each pair of vertices is connected by exactly one arc. In other words, it is an oriented complete graph.
A directed path, or just a path when the context is clear, is an oriented simple path such that all arcs go the same direction, meaning all internal vertices have in- and out-degrees 1. A vertex v is reachable from another vertex u if there is a directed path that starts from u and ends at v. Note that in general the condition that u is reachable from v does not imply that v is also reachable from u.
If v is reachable from u, then u is a predecessor of v and v is a successor of u. If there is an arc from u to v, then u is a direct predecessor of v, and v is a direct successor of u.
A digraph is strongly connected if every vertex is reachable from every other following the directions of the arcs. On the contrary, a digraph is weakly connected if its underlying undirected graph is connected. A weakly connected graph can be thought of as a digraph in which every vertex is "reachable" from every other but not necessarily following the directions of the arcs. A strong orientation is an orientation that produces a strongly connected digraph.
A directed cycle, or just a cycle when the context is clear, is an oriented simple cycle such that all arcs go the same direction, meaning all vertices have in- and out-degrees 1. A digraph is acyclic if it does not contain any directed cycle. A finite, acyclic digraph with no isolated vertices necessarily contains at least one source and at least one sink.
An arborescence, or out-tree or branching, is an oriented tree in which all vertices are reachable from a single vertex. Likewise, an in-tree is an oriented tree in which a single vertex is reachable from every other one.
If there is a directed edge from u to v, then we say u is a parent of v and v is a child of u. If there is a directed path from u to v, we say u is an ancestor of v and v is a descendant of u.
The moral graph
of a DAG is the undirected graph created by adding an (undirected) edge between all parents of the same node (sometimes called marrying), and then replacing all directed edges by undirected edges. A DAG is perfect if, for each node, the set of parents is complete (i.e. no new edges need to be added when forming the moral graph).
Given a graph G (V,E) a k-colouring of G is a map ϕ : V → {1, ... , k} with the property that (u, v) ∈ E ⇒ ϕ(u) ≠ ϕ(v) - in other words, every vertex is assigned a colour with the condition that adjacent vertices cannot be assigned the same colour.
The chromatic number χ(G) is the smallest k for which G has a k-colouring.
Given a graph and a colouring, the colour classes of the graph are the sets of vertices given the same colour.
G, usually a number or a polynomial, that depends only on the isomorphism class of G. Examples are the order, genus, chromatic number, and chromatic polynomial
of a graph.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage.
Basics
A graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G consists of two types of elements, namely vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
and edges. Every edge has two endpoints in the set of vertices, and is said to connect or join the two endpoints. An edge can thus be defined as a set of two vertices (or an ordered pair, in the case of a directed graph - see Section Direction).
Alternative models of graphs exist; e.g., a graph may be thought of as a Boolean binary function
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
over the set of vertices or as a square (0,1)-matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
A vertex is simply drawn as a node or a dot. The vertex set of G is usually denoted by V(G), or V when there is no danger of confusion. The order of a graph is the number of its vertices, i.e. |V(G)|.
An edge (a set of two elements) is drawn as a line connecting two vertices, called endpoints or (less often) endvertices. An edge with endvertices x and y is denoted by xy (without any symbol in between). The edge set of G is usually denoted by E(G), or E when there is no danger of confusion.
The size of a graph is the number of its edges, i.e. |E(G)|.
A loop
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
is an edge whose endpoints are the same vertex. A link has two distinct endvertices. An edge is multiple if there is another edge with the same endvertices; otherwise it is simple. The multiplicity of an edge is the number of multiple edges sharing the same end vertices; the multiplicity of a graph, the maximum multiplicity of its edges. A graph is a simple graph if it has no multiple edges or loops, a multigraph if it has multiple edges, but no loops, and a multigraph or pseudograph if it contains both multiple edges and loops (the literature is highly inconsistent). When stated without any qualification, a graph is almost always assumed to be simple—one has to judge from the context.
Graphs whose edges or vertices have names or labels are known as labeled, those without as unlabeled. Graphs with labeled vertices only are vertex-labeled, those with labeled edges only are edge-labeled. The difference between a labeled and an unlabeled graph is that the latter has no specific set of vertices or edges; it is regarded as another way to look upon an isomorphism type of graphs. (Thus, this usage distinguishes between graphs with identifiable vertex or edge sets on the one hand, and isomorphism types or classes of graphs on the other.)
(Graph labeling
Graph labeling
In the mathematical discipline of graph theory, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices, or both, of a graph....
usually refers to the assignment of labels (usually natural numbers, usually distinct) to the edges and vertices of a graph, subject to certain rules depending on the situation. This should not be confused with a graph's merely having distinct labels or names on the vertices.)

Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
. A simple graph can be considered a special case of the hypergraph, namely the 2-uniform hypergraph. However, when stated without any qualification, an edge is always assumed to consist of at most 2 vertices, and a graph is never confused with a hypergraph.
A non-edge (or anti-edge) is an edge that is not present in the graph. More formally, for two vertices
 and
and  ,
,  is a non-edge in a graph
is a non-edge in a graph 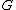 whenever
whenever  is not an edge in
is not an edge in 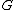 . This means that there is either no edge between the two vertices or (for directed graphs) at most one of
. This means that there is either no edge between the two vertices or (for directed graphs) at most one of  and
and  from
from  is an arc in G.
is an arc in G.Occasionally the term cotriangle or anti-triangle is used for a set of three vertices none of which are connected.
The complement
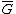 of a graph G is a graph with the same vertex set as G but with an edge set such that xy is an edge in
of a graph G is a graph with the same vertex set as G but with an edge set such that xy is an edge in 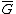 if and only if xy is not an edge in G.
if and only if xy is not an edge in G.An edgeless graph or empty graph or null graph is a graph with zero or more vertices, but no edges. The empty graph or null graph may also be the graph with no vertices and no edges. If it is a graph with no edges and any number
 of vertices, it may be called the null graph on
of vertices, it may be called the null graph on  vertices. (There is no consistency at all in the literature.)
vertices. (There is no consistency at all in the literature.)A graph is infinite if it has infinitely many vertices or edges or both; otherwise the graph is finite. An infinite graph where every vertex has finite degree is called locally finite. When stated without any qualification, a graph is usually assumed to be finite. See also continuous graph.
Two graphs G and H are said to be isomorphic, denoted by G ~ H, if there is a one-to-one correspondence, called an isomorphism, between the vertices of the graph such that two vertices are adjacent in G if and only if their corresponding vertices are adjacent in H. Likewise, a graph G is said to be homomorphic to a graph H if there is a mapping, called a homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
, from V(G) to V(H) such that if two vertices are adjacent in G then their corresponding vertices are adjacent in H.
Subgraphs
A subgraph of a graph G is a graph whose vertex set is a subset of that of G, and whose adjacency relation is a subset of that of G restricted to this subset. In the other direction, a supergraph of a graph G is a graph of which G is a subgraph. We say a graph G contains another graph H if some subgraph of G is H or is isomorphic to H.A subgraph H is a spanning subgraph, or factor, of a graph G if it has the same vertex set as G. We say H spans G.
A subgraph H of a graph G is said to be induced if, for any pair of vertices x and y of H, xy is an edge of H if and only if xy is an edge of G. In other words, H is an induced subgraph of G if it has exactly the edges that appear in G over the same vertex set. If the vertex set of H is the subset S of V(G), then H can be written as G[S] and is said to be induced by S.
A graph that does not contain H as an induced subgraph is said to be H-free.
A universal graph in a class K of graphs is a simple graph in which every element in K can be embedded as a subgraph.
A graph G is minimal with some property P provided that G has property P and no proper subgraph of G has property P. In this definition, the term subgraph is usually understood to mean "induced subgraph." The notion of maximality is defined dually
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
: G is maximal with P provided that P(G) and G has no supergraph H such that P(H).
Many important classes of graphs can be defined by sets of forbidden subgraphs, the minimal graphs that are not in the class.
Walks
A walk is an alternating sequence of vertices and edges, beginning and ending with a vertex, where each vertex is incident to both the edge that precedes it and the edge that follows it in the sequence, and where the vertices that precede and follow an edge are the end vertices of that edge. A walk is closed if its first and last vertices are the same, and open if they are different.The length l of a walk is the number of edges that it uses. For an open walk, l = n–1, where n is the number of vertices visited (a vertex is counted each time it is visited). For a closed walk, l = n (the start/end vertex is listed twice, but is not counted twice). In the example graph, (1, 2, 5, 1, 2, 3) is an open walk with length 5, and (4, 5, 2, 1, 5, 4) is a closed walk of length 5.
A trail is a walk in which all the edges are distinct. A closed trail has been called a tour or circuit, but these are not universal, and the latter is often reserved for a regular subgraph of degree two.

Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
referred to what is now usually known as an open walk. Nowadays, when stated without any qualification, a path is usually understood to be simple, meaning that no vertices (and thus no edges) are repeated. (The term chain has also been used to refer to a walk in which all vertices and edges are distinct.) In the example graph, (5, 2, 1) is a path of length 2. The closed equivalent to this type of walk, a walk that starts and ends at the same vertex but otherwise has no repeated vertices or edges, is called a cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
. Like path, this term traditionally referred to any closed walk, but now is usually understood to be simple by definition. In the example graph, (1, 5, 2, 1) is a cycle of length 3. (A cycle, unlike a path, is not allowed to have length 0.) Paths and cycles of n vertices are often denoted by Pn and Cn, respectively. (Some authors use the length instead of the number of vertices, however.)
C1 is a loop, C2 is a digon (a pair of parallel undirected edges in a multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
, or a pair of antiparallel edges in a directed graph), and C3 is called a triangle.
A cycle that has odd length is an odd cycle; otherwise it is an even cycle. One theorem is that a graph is bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
if and only if it contains no odd cycles. (See complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
.)
A graph is acyclic if it contains no cycles; unicyclic if it contains exactly one cycle; and pancyclic
Pancyclic graph
In the mathematical study of graph theory, a pancyclic graph is a directed or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph...
if it contains cycles of every possible length (from 3 to the order of the graph).
The girth of a graph is the length of a shortest (simple) cycle in the graph; and the circumference, the length of a longest (simple) cycle. The girth and circumference of an acyclic graph are defined to be infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
∞.
A path or cycle is Hamiltonian
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
(or spanning) if it uses all vertices exactly once. A graph that contains a Hamiltonian path is traceable; and one that contains a Hamiltonian path for any given pair of (distinct) end vertices is a Hamiltonian connected graph. A graph that contains a Hamiltonian cycle is a Hamiltonian graph.
A trail or circuit (or cycle) is Eulerian
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...
if it uses all edges precisely once. A graph that contains an Eulerian trail is traversable. A graph that contains an Eulerian circuit is an Eulerian graph.
Two paths are internally disjoint (some people call it independent) if they do not have any vertex in common, except the first and last ones.
A theta graph is the union of three internally disjoint (simple) paths that have the same two distinct end vertices. A theta0 graph has seven vertices which can be arranged as the vertices of a regular hexagon plus an additional vertex in the center. The eight edges are the perimeter of the hexagon plus one diameter.
Trees

Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
is a connected acyclic simple graph. For directed graphs, each vertex has at most one incoming edge. A vertex of degree 1 is called a leaf, or pendant vertex. An edge incident to a leaf is a leaf edge, or pendant edge. (Some people define a leaf edge as a leaf and then define a leaf vertex on top of it. These two sets of definitions are often used interchangeably.) A non-leaf vertex is an internal vertex. Sometimes, one vertex of the tree is distinguished, and called the root; in this case, the tree is called rooted. Rooted trees are often treated as directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
s with the edges pointing away from the root.
A subtree of the tree T is a connected subgraph of T.
A forest is an acyclic simple graph. For directed graphs, each vertex has at most one incoming edge. (That is, a tree with the connectivity requirement removed; a graph containing multiple disconnected trees.)
A subforest of the forest F is a subgraph of F.
A spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
is a spanning subgraph that is a tree. Every graph has a spanning forest. But only a connected graph has a spanning tree.
A special kind of tree called a star
Star (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
is K1,k. An induced star with 3 edges is a claw.
A caterpillar
Caterpillar tree
In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices of the caterpillar are within distance 1 of a central path....
is a tree in which all non-leaf nodes form a single path.
A k-ary tree is a rooted tree in which every internal vertex has k children. A 1-ary tree is just a path. A 2-ary tree is also called a binary tree.
Cliques

Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
Kn of order n is a simple graph with n vertices in which every vertex is adjacent to every other. The example graph to the right is complete. The complete graph on n vertices is often denoted by Kn. It has n(n-1)/2 edges (corresponding to all possible choices of pairs of vertices).
A clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
in a graph is a set of pairwise adjacent vertices. Since any subgraph induced by a clique is a complete subgraph, the two terms and their notations are usually used interchangeably. A k-clique is a clique of order k. In the example graph above, vertices 1, 2 and 5 form a 3-clique, or a triangle. A maximal clique is a clique that is not a subset of any other clique (some authors reserve the term clique for maximal cliques).
The clique number ω(G) of a graph G is the order of a largest clique in G.
Strongly connected component
A related but weaker concept is that of a strongly connected componentStrongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
. Informally, a strongly connected component of a directed graph is a subgraph where all nodes in the subgraph are reachable by all other nodes in the subgraph. Reachability between nodes is established by the existence of a path between the nodes.
A directed graph can be decomposed into strongly connected components by running the depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
(DFS) algorithm twice: first, on the graph itself and next on the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the graph in decreasing order of the finishing times of the first DFS. Given a directed graph G, the transpose GT is the graph G with all the edge directions reversed.
Knots
A knot in a directed graph is a collection of vertices and edges with the property that every vertex in the knot has outgoing edges, and all outgoing edges from vertices in the knot terminate at other vertices in the knot. Thus it is impossible to leave the knot while following the directions of the edges.Minors
A minor of
of 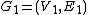 is an injection
is an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from
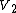 to
to 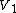 such that every edge in
such that every edge in 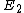 corresponds to a path (disjoint from all other such paths) in
corresponds to a path (disjoint from all other such paths) in 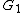 such that every vertex in
such that every vertex in  is in one or more paths, or is part of the injection from
is in one or more paths, or is part of the injection from 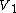 to
to  . This can alternatively be phrased in terms of contractions, which are operations which collapse a path and all vertices on it into a single edge (see Minor (graph theory)
. This can alternatively be phrased in terms of contractions, which are operations which collapse a path and all vertices on it into a single edge (see Minor (graph theory)Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
).
Embedding
An embedding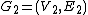 of
of  is an injection
is an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from
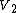 to
to 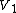 such that every edge in
such that every edge in  corresponds to a path (disjoint from all other such paths) in
corresponds to a path (disjoint from all other such paths) in 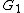 .
.Adjacency and degree
In graph theory, degree, especially that of a vertex, is usually a measure of immediate adjacency.An edge connects two vertices; these two vertices are said to be incident to that edge, or, equivalently, that edge incident to those two vertices. All degree-related concepts have to do with adjacency or incidence.
The degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
, or valency, dG(v) of a vertex v in a graph G is the number of edges incident to v, with loops being counted twice. A vertex of degree 0 is an isolated vertex. A vertex of degree 1 is a leaf. In the labelled simple graph example, vertices 1 and 3 have a degree of 2, vertices 2, 4 and 5 have a degree of 3, and vertex 6 has a degree of 1. If E is finite, then the total sum of vertex degrees is equal to twice the number of edges.
The total degree of a graph is equal to two times the number of edges, loops included. This means that for a graph with 3 vertices with each vertex having a degree of two (i.e. a triangle) the total degree would be six (e.g. 3 x 2 = 6). The general formula for this is total degree = 2n where n = number of edges.
A degree sequence is a list of degrees of a graph in non-increasing order (e.g. d1 ≥ d2 ≥ … ≥ dn). A sequence of non-increasing integers is realizable if it is a degree sequence of some graph.
Two vertices u and v are called adjacent if an edge exists between them. We denote this by u ~ v or u ↓ v. In the above graph, vertices 1 and 2 are adjacent, but vertices 2 and 4 are not. The set of neighbors of v, that is, vertices adjacent to v not including v itself, forms an induced subgraph called the (open) neighborhood
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
of v and denoted NG(v). When v is also included, it is called a closed neighborhood and denoted by NG[v]. When stated without any qualification, a neighborhood is assumed to be open. The subscript G is usually dropped when there is no danger of confusion; the same neighborhood notation may also be used to refer to sets of adjacent vertices rather than the corresponding induced subgraphs. In the example graph, vertex 1 has two neighbors: vertices 2 and 5. For a simple graph, the number of neighbors that a vertex has coincides with its degree.
A dominating set of a graph is a vertex subset whose closed neighborhood includes all vertices of the graph. A vertex v dominates another vertex u if there is an edge from v to u. A vertex subset V dominates another vertex subset U if every vertex in U is adjacent to some vertex in V. The minimum size of a dominating set is the domination number γ(G).
In computers, a finite, directed or undirected graph (with n vertices, say) is often represented by its adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
: an n-by-n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose entry in row i and column j gives the number of edges from the i-th to the j-th vertex.
Spectral graph theory
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
studies relationships between the properties of the graph and its adjacency matrix.
The maximum degree Δ(G) of a graph G is the largest degree over all vertices; the minimum degree δ(G), the smallest.
A graph in which every vertex has the same degree is regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
. It is k-regular if every vertex has degree k. A 0-regular graph is an independent set. A 1-regular graph is a matching. A 2-regular graph is a vertex disjoint union of cycles. A 3-regular graph is said to be cubic, or trivalent.
A k-factor is a k-regular spanning subgraph. A 1-factor is a perfect matching. A partition of edges of a graph into k-factors is called a k-factorization. A k-factorable graph is a graph that admits a k-factorization.
A graph is biregular if it has unequal maximum and minimum degrees and every vertex has one of those two degrees.
A strongly regular graph is a regular graph such that any adjacent vertices have the same number of common neighbors as other adjacent pairs and that any nonadjacent vertices have the same number of common neighbors as other nonadjacent pairs.
Independence
In graph theory, the word independent usually carries the connotation of pairwise disjoint or mutually nonadjacent. In this sense, independence is a form of immediate nonadjacency. An isolated vertex is a vertex not incident to any edges. An independent setIndependent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
, or coclique, or stable set or staset, is a set of vertices of which no pair is adjacent. Since the graph induced by any independent set is an empty graph, the two terms are usually used interchangeably. In the example above, vertices 1, 3, and 6 form an independent set; and 3, 5, and 6 form another one.
Two subgraphs are edge disjoint if they have no edges in common. Similarly, two subgraphs are vertex disjoint if they have no vertices (and thus, also no edges) in common. Unless specified otherwise, a set of disjoint subgraphs are assumed to be pairwise vertex disjoint.
The independence number α(G) of a graph G is the size of the largest independent set of G.
A graph can be decomposed into independent sets in the sense that the entire vertex set of the graph can be partitioned into pairwise disjoint independent subsets. Such independent subsets are called partite sets, or simply parts.
A graph that can be decomposed into two partite sets but not fewer is bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
; three sets but not fewer, tripartite; k sets but not fewer, k-partite; and an unknown number of sets, multipartite. An 1-partite graph is the same as an independent set, or an empty graph. A 2-partite graph is the same as a bipartite graph. A graph that can be decomposed into k partite sets is also said to be k-colourable.
A complete multipartite graph is a graph in which vertices are adjacent if and only if they belong to different partite sets. A complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
is also referred to as a biclique; if its partite sets contain n and m vertices, respectively, then the graph is denoted Kn,m.
A k-partite graph is semiregular if each of its partite sets has a uniform degree; equipartite if each partite set has the same size; and balanced k-partite if each partite set differs in size by at most 1 with any other.
The matching number
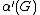 of a graph G is the size of a largest matching, or pairwise vertex disjoint edges, of G.
of a graph G is the size of a largest matching, or pairwise vertex disjoint edges, of G.A spanning matching, also called a perfect matching is a matching that covers all vertices of a graph.
Connectivity
ConnectivityConnectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
extends the concept of adjacency and is essentially a form (and measure) of concatenated adjacency.
If it is possible to establish a path from any vertex to any other vertex of a graph, the graph is said to be connected; otherwise, the graph is disconnected. A graph is totally disconnected if there is no path connecting any pair of vertices. This is just another name to describe an empty graph or independent set.
A cut vertex, or articulation point, is a vertex whose removal disconnects the remaining subgraph. A cut set, or vertex cut or separating set, is a set of vertices whose removal disconnects the remaining subgraph. A bridge is an analogous edge (see below).
If it is always possible to establish a path from any vertex to every other even after removing any k - 1 vertices, then the graph is said to be k-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
or k-connected. Note that a graph is k-connected if and only if it contains k internally disjoint paths between any two vertices. The example graph above is connected (and therefore 1-connected), but not 2-connected. The vertex connectivity or connectivity κ(G) of a graph G is the minimum number of vertices that need to be removed to disconnect G. The complete graph Kn has connectivity n - 1 for n > 1; and a disconnected graph has connectivity 0.
In network theory
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
, a giant component
Giant component
In network theory, a giant component is a connected component of a given random graph that contains a constant fraction of the entire graph's vertices....
is a connected subgraph that contains a majority of the entire graph's nodes
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
.
A bridge
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
, or cut edge or isthmus, is an edge whose removal disconnects a graph. (For example, all the edges in a tree are bridges.) A disconnecting set is a set of edges whose removal increases the number of components. An edge cut is the set of all edges which have one vertex in some proper vertex subset S and the other vertex in V(G)\S. Edges of K3 form a disconnecting set but not an edge cut. Any two edges of K3 form a minimal
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
disconnecting set as well as an edge cut. An edge cut is necessarily a disconnecting set; and a minimal disconnecting set of a nonempty graph is necessarily an edge cut. A bond is a minimal (but not necessarily minimum), nonempty set of edges whose removal disconnects a graph. A cut vertex is an analogous vertex (see above).
A graph is k-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
if any subgraph formed by removing any k - 1 edges is still connected. The edge connectivity κ'(G) of a graph G is the minimum number of edges needed to disconnect G. One well-known result is that κ(G) ≤ κ'(G) ≤ δ(G).
A component is a maximally connected subgraph. A block is either a maximally 2-connected subgraph, a bridge (together with its vertices), or an isolated vertex. A biconnected component
Biconnected component
In graph theory, a biconnected component is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points...
is a 2-connected component.
An articulation point (also known as a separating vertex) of a graph is a vertex whose removal from the graph increases its number of connected components. A biconnected component can be defined as a subgraph induced by a maximal set of nodes that has no separating vertex.
Distance
The distanceDistance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
dG(u, v) between two (not necessary distinct) vertices u and v in a graph G is the length of a shortest path between them. The subscript G is usually dropped when there is no danger of confusion. When u and v are identical, their distance is 0. When u and v are unreachable from each other, their distance is defined to be infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
∞.
The eccentricity εG(v) of a vertex v in a graph G is the maximum distance from v to any other vertex. The diameter diam(G) of a graph G is the maximum eccentricity over all vertices in a graph; and the radius rad(G), the minimum. When there are two components in G, diam(G) and rad(G) defined to be infinity ∞. Trivially, diam(G) ≤ 2 rad(G). Vertices with maximum eccentricity are called peripheral vertices. Vertices of minimum eccentricity form the center. A tree has at most two center vertices.
The Wiener index of a vertex v in a graph G, denoted by WG(v) is the sum of distances between v and all others. The Wiener index of a graph G, denoted by W(G), is the sum of distances over all pairs of vertices. An undirected graph's Wiener polynomial is defined to be Σ qd(u,v) over all unordered pairs of vertices u and v. Wiener index and Wiener polynomial are of particular interest to mathematical chemists.
The k-th power Gk of a graph G is a supergraph formed by adding an edge between all pairs of vertices of G with distance at most k. A second power of a graph is also called a square.
A k-spanner is a spanning subgraph, S, in which every two vertices are at most k times as far apart on S than on G. The number k is the dilation. k-spanner is used for studying geometric network optimization.
Genus
A crossing is a pair of intersecting edges. A graph is embeddable on a surface if its vertices and edges can be arranged on it without any crossing. The genus of a graph is the lowest genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of any surface on which the graph can embed.
A planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
is one which can be drawn on the (Euclidean) plane without any crossing; and a plane graph, one which is drawn in such fashion. In other words, a planar graph is a graph of genus 0. The example graph is planar; the complete graph on n vertices, for n> 4, is not planar. Also, a tree is necessarily a planar graph.
When a graph is drawn without any crossing, any cycle that surrounds a region without any edges reaching from the cycle into the region forms a face. Two faces on a plane graph are adjacent if they share a common edge. A dual, or planar dual when the context needs to be clarified, G* of a plane graph G is a graph whose vertices represent the faces, including any outerface, of G and are adjacent in G* if and only if their corresponding faces are adjacent in G. The dual of a planar graph is always a planar pseudograph (e.g. consider the dual of a triangle). In the familiar case of a 3-connected simple planar graph G (isomorphic to a convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
P), the dual G* is also a 3-connected simple planar graph (and isomorphic to the dual polyhedron P*).
Furthermore, since we can establish a sense of "inside" and "outside" on a plane, we can identify an "outermost" region that contains the entire graph if the graph does not cover the entire plane. Such outermost region is called an outer face. An outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
is one which can be drawn in the planar fashion such that its vertices are all adjacent to the outer face; and an outerplane graph, one which is drawn in such fashion.
The minimum number of crossings that must appear when a graph is drawn on a plane is called the crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
.
The minimum number of planar graphs needed to cover a graph is the thickness of the graph.
Weighted graphs and networks
A weighted graph associates a label (weight) with every edge in the graph. Weights are usually real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. They may be restricted to rational numbers or integers. Certain algorithms require further restrictions on weights; for instance, Dijkstra's algorithm
Dijkstra's algorithm
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
works properly only for positive weights. The weight of a path or the weight of a tree in a weighted graph is the sum of the weights of the selected edges. Sometimes a non-edge is labeled by a special weight representing infinity. Sometimes the word cost is used instead of weight. When stated without any qualification, a graph is always assumed to be unweighted. In some writing on graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
the term network is a synonym for a weighted graph. A network may be directed or undirected, it may contain special vertices (nodes), such as source or sink. The classical network problems include:
- minimum cost spanning tree,
- shortest paths,
- maximal flow (and the max-flow min-cut theoremMax-flow min-cut theoremIn optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
)
Direction
A directed arc, or directed edge, is an ordered pair of endvertices that can be represented graphically as an arrow drawn between the endvertices. In such an ordered pair the first vertex is called the initial vertex or tail; the second one is called the terminal vertex or head (because it appears at the arrow head). An undirected edge disregards any sense of direction and treats both endvertices interchangeably. A loop in a digraph, however, keeps a sense of direction and treats both head and tail identically. A set of arcs are multiple, or parallel, if they share the same head and the same tail. A pair of arcs are anti-parallel if one's head/tail is the other's tail/head. A digraph, or directed graph, or oriented graph, is analogous to an undirected graph except that it contains only arcs. A mixed graph may contain both directed and undirected edges; it generalizes both directed and undirected graphs. When stated without any qualification, a graph is almost always assumed to be undirected.A digraph is called simple if it has no loops and at most one arc between any pair of vertices. When stated without any qualification, a digraph is usually assumed to be simple.
In a digraph Γ, we distinguish the out degree dΓ+(v), the number of edges leaving a vertex v, and the in degree dΓ-(v), the number of edges entering a vertex v. If the graph is oriented, the degree dΓ(v) of a vertex v is equal to the sum of its out- and in- degrees. When the context is clear, the subscript Γ can be dropped. Maximum and minimum out degrees are denoted by Δ+(Γ) and δ+(Γ); and maximum and minimum in degrees, Δ-(Γ) and δ-(Γ).
An out-neighborhood, or successor set, N+Γ(v) of a vertex v is the set of heads of arcs going from v. Likewise, an in-neighborhood, or predecessor set, N-Γ(v) of a vertex v is the set of tails of arcs going into v.
A source is a vertex with 0 in-degree; and a sink, 0 out-degree.
A vertex v dominates another vertex u if there is an arc from v to u. A vertex subset S is out-dominating if every vertex not in S is dominated by some vertex in S; and in-dominating if every vertex in S is dominated by some vertex not in S.
A kernel is an independent out-dominating set. A digraph is kernel perfect if every induced sub-digraph has a kernel.
An Eulerian digraph is a digraph with equal in- and out-degrees at every vertex.
The zweieck of an undirected edge
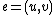 is the pair of diedges
is the pair of diedges and
and  which form the simple dicircuit.
which form the simple dicircuit.An orientation is an assignment of directions to the edges of an undirected or partially directed graph. When stated without any qualification, it is usually assumed that all undirected edges are replaced by a directed one in an orientation. Also, the underlying graph is usually assumed to be undirected and simple.
A tournament
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
is a digraph in which each pair of vertices is connected by exactly one arc. In other words, it is an oriented complete graph.
A directed path, or just a path when the context is clear, is an oriented simple path such that all arcs go the same direction, meaning all internal vertices have in- and out-degrees 1. A vertex v is reachable from another vertex u if there is a directed path that starts from u and ends at v. Note that in general the condition that u is reachable from v does not imply that v is also reachable from u.
If v is reachable from u, then u is a predecessor of v and v is a successor of u. If there is an arc from u to v, then u is a direct predecessor of v, and v is a direct successor of u.
A digraph is strongly connected if every vertex is reachable from every other following the directions of the arcs. On the contrary, a digraph is weakly connected if its underlying undirected graph is connected. A weakly connected graph can be thought of as a digraph in which every vertex is "reachable" from every other but not necessarily following the directions of the arcs. A strong orientation is an orientation that produces a strongly connected digraph.
A directed cycle, or just a cycle when the context is clear, is an oriented simple cycle such that all arcs go the same direction, meaning all vertices have in- and out-degrees 1. A digraph is acyclic if it does not contain any directed cycle. A finite, acyclic digraph with no isolated vertices necessarily contains at least one source and at least one sink.
An arborescence, or out-tree or branching, is an oriented tree in which all vertices are reachable from a single vertex. Likewise, an in-tree is an oriented tree in which a single vertex is reachable from every other one.
Directed acyclic graphs
The partial order structure of directed acyclic graphs (or DAGs) gives them their own terminology.If there is a directed edge from u to v, then we say u is a parent of v and v is a child of u. If there is a directed path from u to v, we say u is an ancestor of v and v is a descendant of u.
The moral graph
Moral graph
A moral graph is a concept in graph theory, used to find the equivalent undirected form of a directed acyclic graph. It is a key step of the junction tree algorithm, used in belief propagation on graphical models....
of a DAG is the undirected graph created by adding an (undirected) edge between all parents of the same node (sometimes called marrying), and then replacing all directed edges by undirected edges. A DAG is perfect if, for each node, the set of parents is complete (i.e. no new edges need to be added when forming the moral graph).
Colouring
Vertices in graphs can be given colours to identify or label them. Although they may actually be rendered in diagrams in different colours, working mathematicians generally pencil in numbers or letters (usually numbers) to represent the colours.Given a graph G (V,E) a k-colouring of G is a map ϕ : V → {1, ... , k} with the property that (u, v) ∈ E ⇒ ϕ(u) ≠ ϕ(v) - in other words, every vertex is assigned a colour with the condition that adjacent vertices cannot be assigned the same colour.
The chromatic number χ(G) is the smallest k for which G has a k-colouring.
Given a graph and a colouring, the colour classes of the graph are the sets of vertices given the same colour.
Various
A graph invariant is a property of a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G, usually a number or a polynomial, that depends only on the isomorphism class of G. Examples are the order, genus, chromatic number, and chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
of a graph.

