
Outerplanar graph
Encyclopedia
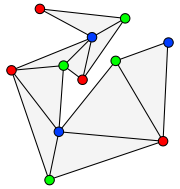
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an undirected graph is an outerplanar graph if it can be drawn
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
in the plane without crossings
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges. Alternatively, a graph G is outerplanar if the graph formed from G by adding a new vertex, with edges connecting it to all the other vertices, is a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
.
History
Outerplanar graphs were first studied and named by , in connection with the problem of determining the planarity of graphs formed by using a perfect matching to connect together two copies of a base graph (for instance, many of the generalized Petersen graphGeneralized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
s are formed in this way from two copies of a cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
). As they showed, when the base graph is biconnected
Biconnected graph
In the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...
, a graph constructed in this way is planar if and only if its base graph is outerplanar and the matching forms a dihedral
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
permutation of its outer cycle.
Forbidden graph characterizations
Outerplanar graphs have a forbidden graph characterization analogous to Kuratowski's theorem and Wagner's theorem for planar graphs: a graph is outerplanar if and only if it does not contain a subdivisionHomeomorphism (graph theory)
In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K4 or the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K2,3. Alternatively, a graph is outerplanar if and only if it does not contain K4 or K2,3 as a minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
, a graph obtained from it by deleting and contracting edges.
A triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
is outerplanar if and only if it does not contain a subdivision of K2,3.
Biconnectivity and Hamiltonicity
An outerplanar graph is biconnectedBiconnected graph
In the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...
if and only if the outer face of the graph forms a simple cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
without repeated vertices. An outerplanar graph is Hamiltonian if and only if it is biconnected; in this case, the outer face forms the unique Hamiltonian cycle. More generally, the size of the longest cycle in an outerplanar graph is the same as the number of vertices in its largest biconnected component
Biconnected component
In graph theory, a biconnected component is a maximal biconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points...
. For this reason finding Hamiltonian cycles and longest cycles in outerplanar graphs may be solved in linear time, in contrast to the NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
ness of these problems for arbitrary graphs.
Every maximal outerplanar graph satisfies a stronger condition than Hamiltonicity: it is node pancyclic
Pancyclic graph
In the mathematical study of graph theory, a pancyclic graph is a directed or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph...
, meaning that for every vertex v and every k in the range from three to the number of vertices in the graph, there is a length-k cycle containing v. A cycle of this length may be found by repeatedly removing a triangle that is connected to the rest of the graph by a single edge, such that the removed vertex is not v, until the outer face of the remaining graph has length k.
A planar graph is outerplanar if and only if each of its biconnected components is outerplanar.
Coloring
All loopless outerplanar graphs can be coloredGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
using only three colors; this fact features prominently in the simplified proof of Chvátal's
Václav Chvátal
Václav Chvátal is a professor in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Canada, where he holds theCanada Research Chair in Combinatorial Optimization....
art gallery theorem by . A 3-coloring may be found in linear time by a greedy coloring
Greedy coloring
In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...
algorithm that removes any vertex of degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
at most two, colors the remaining graph recursively, and then adds back the removed vertex with a color different from the colors of its two neighbors.
According to Vizing's theorem, the chromatic index of any graph (the minimum number of colors needed to color its edges so that no two adjacent edges have the same color) is either the maximum degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of any vertex of the graph or one plus the maximum degree. However, in an outerplanar graph, the chromatic index is equal to the maximum degree except when the graph forms a cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
of odd length. An edge coloring with an optimal number of colors can be found in linear time based on a breadth-first traversal of the weak dual tree.
Related families of graphs
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
.
Every outerplanar graph is also a subgraph of a series-parallel graph
Series-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
. However, not all planar graphs and series-parallel graphs are outerplanar: the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K4 is planar but neither series-parallel nor outerplanar, and the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K2,3 is planar and series-parallel but not outerplanar. Every forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, and every cactus graph
Cactus graph
In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block is an edge or a cycle.-Properties:Cacti are outerplanar graphs...
is outerplanar.
The weak planar dual graph of an embedded outerplanar graph (the graph that has a vertex for every bounded face of the embedding, and an edge for every pair of adjacent bounded faces) is a forest, and the weak planar dual of a Halin graph
Halin graph
In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...
is an outerplanar graph. A planar graph is outerplanar if and only if its weak dual is a forest, and it is Halin if and only if its weak dual is biconnected and outerplanar.
A 1-outerplanar embedding of a graph is the same as an outerplanar embedding. For k > 1 a planar embedding is said to be k-outerplanar if removing the vertices on the outer face results in a (k − 1)-outerplanar embedding. A graph is k-outerplanar if it has a k-outerplanar embedding.
A maximal outerplanar graph is an outerplanar graph that cannot have any additional edges added to it while preserving outerplanarity. Every maximal outerplanar graph with n vertices has exactly 2n − 3 edges, and every bounded face of a maximal outerplanar graph is a triangle. An outerplanar graph is a chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
if and only if it is maximal outerplanar. Every maximal planar graph is the visibility graph
Visibility graph
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them...
of a simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
. Maximal outerplanar graphs are also formed as the graphs of polygon triangulation
Polygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
s. They are examples of 2-trees
K-tree
In graph theory, a k-tree is a chordal graph all of whose maximal cliques are the same size k + 1 and all of whose minimal clique separators are also all the same size k....
, of series-parallel graph
Series-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
s, and of chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
s.
Every outerplanar graph is a circle graph
Circle graph
In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.-Algorithmic...
, the intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
of a set of chords of a circle.
Other properties
Outerplanar graphs have degeneracyDegeneracy (graph theory)
In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
at most two: every subgraph of an outerplanar graph contains a vertex with degree at most two.
Outerplanar graphs have treewidth at most two, which implies that many graph optimization problems that are NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
for arbitrary graphs may be solved in polynomial time by dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
when the input is outerplanar. More generally, k-outerplanar graphs have treewidth O(k).
Every outerplanar graph can be represented as an intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
of axis-aligned rectangles in the plane, so outerplanar graphs have boxicity
Boxicity
In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.The boxicity of a graph is the minimum dimension in which a given graph can be represented as an intersection graph of axis-parallel boxes...
at most two.
A graph is outerplanar if and only if its Colin de Verdière graph invariant
Colin de Verdière graph invariant
Colin de Verdière's invariant is a graph parameter \mu for any graph G introduced by Yves Colin de Verdière in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.-Definition:...
is at most two. The graphs characterized in a similar way by having Colin de Verdière invariant at most one, three, or four are respectively the linear forests, planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, and
linklessly embeddable graphs
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
.

