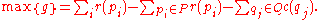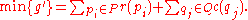Max-flow min-cut theorem
Encyclopedia
In optimization theory
, the max-flow min-cut theorem states that in a flow network
, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the sink.
The max-flow min-cut theorem is a special case of the duality theorem and can be used to derive Menger's theorem
and the König-Egerváry Theorem
.
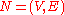 be a network (directed graph) with
be a network (directed graph) with  and
and  being the source and the sink of
being the source and the sink of  respectively.
respectively.
The maximum flow problem is to maximize | f |, that is, to route as much flow as possible from s to t.
The minimum cut problem is to minimize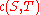 , that is, to determine S and T such that the capacity of the S-T cut is minimal.
, that is, to determine S and T such that the capacity of the S-T cut is minimal.
The equality in the max-flow min-cut theorem follows from the strong duality theorem, which states that if the primal program has an optimal solution, x*, then the dual program also has an optimal solution, y*, such that the optimal values formed by the two solutions are equal.
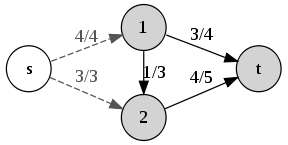 The figure on the right is a network having a value of flow of 7. The vertex in white and the vertices in grey form the subsets S and T of an s-t cut, whose cut-set contains the dashed edges. Since the capacity of the s-t cut is 7, which is equal to the value of flow, the max-flow min-cut theorem tells us that the value of flow and the capacity of the s-t cut are both optimal in this network.
The figure on the right is a network having a value of flow of 7. The vertex in white and the vertices in grey form the subsets S and T of an s-t cut, whose cut-set contains the dashed edges. Since the capacity of the s-t cut is 7, which is equal to the value of flow, the max-flow min-cut theorem tells us that the value of flow and the capacity of the s-t cut are both optimal in this network.
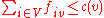 for each
for each 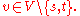
In other words, the amount of flow passing through a vertex cannot exceed its capacity. Define an s-t cut to be the set of vertices and edges such that for any path from s to t, the path contains a member of the cut. In this case, the capacity of the cut is the sum the capacity of each edge and vertex in it.
In this new definition, the generalized max-flow min-cut theorem states that the maximum value of an s-t flow is equal to the minimum capacity of an s-t cut in the new sense.
The Menger's theorem states that the maximum number of edge-disjoint s-t paths in an undirected graph is equal to the minimum number of edges in an s-t cut-set.
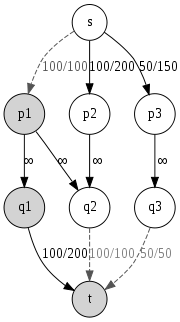 In the project selection problem, there are
In the project selection problem, there are  projects and
projects and  equipments. Each project
equipments. Each project 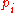 yields revenue
yields revenue 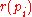 and each equipment
and each equipment 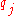 costs
costs 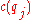 to purchase. Each project requires a number of equipments and each equipment can be shared by several projects. The problem is to determine which projects and equipments should be selected and purchased respectively, so that the profit is maximized.
to purchase. Each project requires a number of equipments and each equipment can be shared by several projects. The problem is to determine which projects and equipments should be selected and purchased respectively, so that the profit is maximized.
Let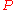 be the set of projects not selected and
be the set of projects not selected and  be the set of equipments purchased, then the problem can be formulated as,
be the set of equipments purchased, then the problem can be formulated as,
Since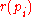 and
and 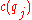 are positive, this maximization problem can be formulated as a minimization problem instead, that is,
are positive, this maximization problem can be formulated as a minimization problem instead, that is,
The above minimization problem can then be formulated as a minimum-cut problem by constructing a network, where the source is connected to the projects with capacity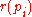 , and the sink is connected by the equipments with capacity
, and the sink is connected by the equipments with capacity 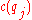 . An edge (
. An edge (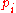 ,
, 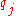 ) with infinite capacity is added if project
) with infinite capacity is added if project 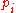 requires equipment
requires equipment 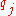 . The s-t cut-set represents the projects and equipments in
. The s-t cut-set represents the projects and equipments in 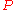 and
and  respectively. By the max-flow min-cut theorem, one can solve the problem as a maximum flow problem
respectively. By the max-flow min-cut theorem, one can solve the problem as a maximum flow problem
.
The figure on the right gives a network formulation of the following project selection problem:
The minimum capacity of a s-t cut is 250 and the sum of the revenue of each project is 450; therefore the maximum profit g is 450 − 250 = 200, by selecting projects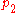 and
and 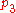 .
.
, A. Feinstein, and C.E. Shannon in 1956, and independently also by L.R. Ford, Jr. and D.R. Fulkerson in the same year.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, the max-flow min-cut theorem states that in a flow network
Flow network
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the sink.
The max-flow min-cut theorem is a special case of the duality theorem and can be used to derive Menger's theorem
Menger's theorem
In the mathematical discipline of graph theory and related areas, Menger's theorem is a basic result about connectivity in finite undirected graphs. It was proved for edge-connectivity and vertex-connectivity by Karl Menger in 1927...
and the König-Egerváry Theorem
König's theorem (graph theory)
In the mathematical area of graph theory, König's theorem, proved by Dénes Kőnig in 1931, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs...
.
Definition
Let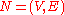 be a network (directed graph) with
be a network (directed graph) with  and
and  being the source and the sink of
being the source and the sink of  respectively.
respectively.- The capacity of an edge is a mapping c: E→R+, denoted by cuv or c(u,v). It represents the maximum amount of flow that can pass through an edge.
- A flow is a mapping f: E→R+, denoted by fuv or f(u,v), subject to the following two constraints:
-
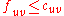 for each
for each 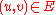 (capacity constraint)
(capacity constraint) -
 for each
for each  (conservation of flows).
(conservation of flows).
-
- The value of flow is defined by
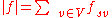 , where s is the source of N. It represents the amount of flow passing from the source to the sink.
, where s is the source of N. It represents the amount of flow passing from the source to the sink.
The maximum flow problem is to maximize | f |, that is, to route as much flow as possible from s to t.
- An s-t cut C = (S,T) is a partition of V such that s∈S and t∈T. The cut-set of C is the set {(u,v)∈E | u∈S, v∈T}. Note that if the edges in the cut-set of C are removed, | f | = 0.
- The capacity of an s-t cut is defined by
 .
.
The minimum cut problem is to minimize
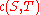 , that is, to determine S and T such that the capacity of the S-T cut is minimal.
, that is, to determine S and T such that the capacity of the S-T cut is minimal.Statement
The max-flow min-cut theorem states- The maximum value of an s-t flow is equal to the minimum capacity of an s-t cut.
Linear program formulation
The max-flow problem and min-cut problem can be formulated as two primal-dual linear programs.Max-flow (Primal) |
Min-cut (Dual) |
|---|---|
maximize 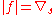 |
minimize  |
subject to 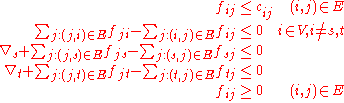 |
subject to  |
The equality in the max-flow min-cut theorem follows from the strong duality theorem, which states that if the primal program has an optimal solution, x*, then the dual program also has an optimal solution, y*, such that the optimal values formed by the two solutions are equal.
Example

Generalized max-flow min-cut theorem
In addition to edge capacity, consider there is capacity at each vertex, that is, a mapping c: V→R+, denoted by c(v), such that the flow f has to satisfy not only the capacity constraint and the conservation of flows, but also the vertex capacity constraint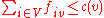 for each
for each 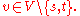
In other words, the amount of flow passing through a vertex cannot exceed its capacity. Define an s-t cut to be the set of vertices and edges such that for any path from s to t, the path contains a member of the cut. In this case, the capacity of the cut is the sum the capacity of each edge and vertex in it.
In this new definition, the generalized max-flow min-cut theorem states that the maximum value of an s-t flow is equal to the minimum capacity of an s-t cut in the new sense.
Menger's theorem
In the undirected edge-disjoint paths problem, we are given an undirected graph G = (V, E) and two vertices s and t, and we have to find the maximum number of edge-disjoint s-t paths in G.The Menger's theorem states that the maximum number of edge-disjoint s-t paths in an undirected graph is equal to the minimum number of edges in an s-t cut-set.
Project selection problem

 projects and
projects and  equipments. Each project
equipments. Each project 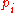 yields revenue
yields revenue 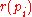 and each equipment
and each equipment 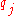 costs
costs 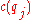 to purchase. Each project requires a number of equipments and each equipment can be shared by several projects. The problem is to determine which projects and equipments should be selected and purchased respectively, so that the profit is maximized.
to purchase. Each project requires a number of equipments and each equipment can be shared by several projects. The problem is to determine which projects and equipments should be selected and purchased respectively, so that the profit is maximized.Let
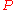 be the set of projects not selected and
be the set of projects not selected and  be the set of equipments purchased, then the problem can be formulated as,
be the set of equipments purchased, then the problem can be formulated as,Since
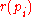 and
and 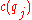 are positive, this maximization problem can be formulated as a minimization problem instead, that is,
are positive, this maximization problem can be formulated as a minimization problem instead, that is,The above minimization problem can then be formulated as a minimum-cut problem by constructing a network, where the source is connected to the projects with capacity
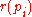 , and the sink is connected by the equipments with capacity
, and the sink is connected by the equipments with capacity 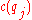 . An edge (
. An edge (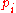 ,
, 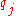 ) with infinite capacity is added if project
) with infinite capacity is added if project 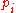 requires equipment
requires equipment 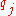 . The s-t cut-set represents the projects and equipments in
. The s-t cut-set represents the projects and equipments in 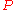 and
and  respectively. By the max-flow min-cut theorem, one can solve the problem as a maximum flow problem
respectively. By the max-flow min-cut theorem, one can solve the problem as a maximum flow problemMaximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum....
.
The figure on the right gives a network formulation of the following project selection problem:
Project 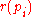 |
Equipment 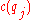 |
||
|---|---|---|---|
| 1 | 100 | 200 | Project 1 requires equipments 1 and 2. |
| 2 | 200 | 100 | Project 2 requires equipment 2. |
| 3 | 150 | 50 | Project 3 requires equipment 3. |
The minimum capacity of a s-t cut is 250 and the sum of the revenue of each project is 450; therefore the maximum profit g is 450 − 250 = 200, by selecting projects
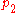 and
and 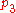 .
.History
The max-flow min-cut theorem was proved by P. EliasPeter Elias
Peter Elias was a pioneer in the field of information theory. Born in New Brunswick, New Jersey, he was a member of the Massachusetts Institute of Technology faculty from 1953 to 1991....
, A. Feinstein, and C.E. Shannon in 1956, and independently also by L.R. Ford, Jr. and D.R. Fulkerson in the same year.
See also
- Linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
- Maximum flow
- Minimum cutMinimum cutIn graph theory, a minimum cut of a graph is a cut whose cutset has the smallest number of elements or smallest sum of weights possible...
- Flow networkFlow networkIn graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
- Edmonds-Karp algorithmEdmonds-Karp algorithmIn computer science and graph theory, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in O time. It is asymptotically slower than the relabel-to-front algorithm, which runs in O time, but it is often faster in...