Graph labeling
Encyclopedia
In the mathematical discipline of graph theory
, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices
, or both, of a graph
.
Formally, given a graph G, a vertex labeling is a function mapping vertices of G to a set of labels. A graph with such a function defined is called a vertex-labeled graph. Likewise, an edge labeling is a function mapping edges of G to a set of "labels". In this case, G is called an edge-labeled graph.
When the edge labels are members of an ordered set (e.g., the real number
s), it may be called a weighted graph.
When used without qualification, the term labeled graph generally refers to a vertex-labeled graph with all labels distinct. Such a graph may equivalently be labeled by the consecutive integers {1, ..., n}, where n is the number of vertices in the graph.
For many applications, the edges or vertices are given labels that are meaningful in the associated domain. For example, the edges may be assigned weights representing the "cost" of traversing between the incident vertices.
In the above definition a graph is understood to be a finite undirected simple graph. However, the notion of labeling may be applied to all extensions and generalizations of graphs. For example, in automata theory
and formal language
theory it is convenient to consider labeled multigraph
s, i.e., a pair of vertices may be connected by several labeled edges.
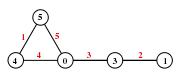A graph is known as graceful when it vertices are labeled from 0 to 
, the size of the graph, and this labeling induces an edge labeling from 1 to 
. For any edge e, es label is the positive difference between the two vertices incident with e. In other words, if e is incident with vertices labeled k and j, e will be labeled 
. Thus, a graph 
is graceful if and only if there exists an injection that induces a bijection from E to the positive integers up to 
.
In his original paper, Rosa proved that all eulerian graphs with order equivalent
to 1 or 2 (mod
4) are not graceful. Whether or not certain families of graphs are graceful is an area of graph theory under extensive study. Arguably, the largest unproven conjecture in Graph Labeling is the Ringel-Kotzig conjecture, which hypothesizes that all trees are graceful. This has been proven for all paths
, caterpillars
, and many other infinite families of trees. Kotzig himself has called the effort to prove the conjecture a "disease."
vertices of G to the group
of integers modulo
k that induces a bijection between the edges of G and the positive integers up to
. For any edge e, es label is the sum of the labels of the two vertices incident with e (mod q).
is a special case of graph labelings, such that adjacent vertices and coincident edges must have different labels.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, or both, of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
.
Formally, given a graph G, a vertex labeling is a function mapping vertices of G to a set of labels. A graph with such a function defined is called a vertex-labeled graph. Likewise, an edge labeling is a function mapping edges of G to a set of "labels". In this case, G is called an edge-labeled graph.
When the edge labels are members of an ordered set (e.g., the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s), it may be called a weighted graph.
When used without qualification, the term labeled graph generally refers to a vertex-labeled graph with all labels distinct. Such a graph may equivalently be labeled by the consecutive integers {1, ..., n}, where n is the number of vertices in the graph.
For many applications, the edges or vertices are given labels that are meaningful in the associated domain. For example, the edges may be assigned weights representing the "cost" of traversing between the incident vertices.
In the above definition a graph is understood to be a finite undirected simple graph. However, the notion of labeling may be applied to all extensions and generalizations of graphs. For example, in automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
and formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory it is convenient to consider labeled multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s, i.e., a pair of vertices may be connected by several labeled edges.
History
Most graph labelings trace their origins to labelings presented by Alex Rosa in his 1967 paper. Rosa identified three types of labelings, which he called α-, β-, and ρ-labelings. β-Labelings were later renamed graceful by S.W. Golomb and the name has been popular since.Graceful labeling
, the size of the graph, and this labeling induces an edge labeling from 1 to . For any edge e, es label is the positive difference between the two vertices incident with e. In other words, if e is incident with vertices labeled k and j, e will be labeled . Thus, a graph is graceful if and only if there exists an injection that induces a bijection from E to the positive integers up to .In his original paper, Rosa proved that all eulerian graphs with order equivalent
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
to 1 or 2 (mod
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
4) are not graceful. Whether or not certain families of graphs are graceful is an area of graph theory under extensive study. Arguably, the largest unproven conjecture in Graph Labeling is the Ringel-Kotzig conjecture, which hypothesizes that all trees are graceful. This has been proven for all paths
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
, caterpillars
Caterpillar tree
In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices of the caterpillar are within distance 1 of a central path....
, and many other infinite families of trees. Kotzig himself has called the effort to prove the conjecture a "disease."
Harmonious labelings
A harmonious graph is a graph with k edges that permits an injection from thevertices of G to the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of integers modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
k that induces a bijection between the edges of G and the positive integers up to
. For any edge e, es label is the sum of the labels of the two vertices incident with e (mod q).Graph coloring
Graph coloringGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
is a special case of graph labelings, such that adjacent vertices and coincident edges must have different labels.