Eulerian path - AbsoluteAstronomy.com

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

. They were first discussed by Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

while solving the famous Seven Bridges of Königsberg

Seven Bridges of Königsberg

The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology....

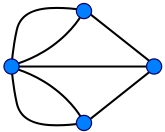
problem in 1736. Mathematically the problem can be stated like this:

Given the graph on the right, is it possible to construct a path (or a cycle

Cycle (graph theory)

In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

, i.e. a path starting and ending on the same vertex) which visits each edge exactly once?

Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

, and stated without proof that connected graphs with all vertices of even degree have a Eulerian circuit. The first complete proof of this latter claim was published posthumously in 1873 by Carl Hierholzer

Carl Hierholzer

Carl Hierholzer was a German mathematician.-Biography:Hierholzer studied mathematics in Karlsruhe, and he got his Ph.D. from Ruprecht-Karls-Universität Heidelberg in 1865. His Ph.D. advisor was Ludwig Otto Hesse...

.

The term Eulerian graph has two common meanings in graph theory. One meaning is a graph with a Eulerian circuit, and the other is a graph with every vertex of even degree. These definitions coincide for connected graphs.

For the existence of Eulerian trails it is necessary that no more than two vertices have an odd degree; this means the Königsberg graph is not Eulerian. If there are no vertices of odd degree, all Eulerian trails are circuits. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other. Sometimes a graph that has a Eulerian trail but not a Eulerian circuit is called semi-Eulerian.

Definition

An Eulerian trail, or Euler walk in an undirected graph is a path

Path (graph theory)

In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

that uses each edge exactly once. If such a path exists, the graph is called traversable or semi-eulerian.

An Eulerian cycle, Eulerian circuit or Euler tour in an undirected graph is a cycle

Cycle (graph theory)

that uses each edge exactly once. If such a cycle exists, the graph is called unicursal. While such graphs are Eulerian graphs, not every Eulerian graph possesses a Eulerian cycle.

For directed graph

Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

s, "path" has to be replaced with directed path and "cycle" with directed cycle.

The definition and properties of Eulerian trails, cycles and graphs are valid for multigraph

Multigraph

In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....

s as well.

An Eulerian orientation of an undirected graph G is an assignment of a direction to each edge of G such that, at each vertex v, the indegree of v equals the outdegree of v. Such an orientation exists for any undirected graph in which every vertex has even degree, and may be found by constructing an Euler tour in each connected component of G and then orienting the edges according to the tour. Every Eulerian orientation of a connected graph is a strong orientation, an orientation that makes the resulting directed graph strongly connected.

Properties

An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...

.
An undirected graph can be decomposed into edge-disjoint cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

s if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
An undirected graph has an Eulerian trail if and only if at most two vertices have odd degree, and if all of its vertices with nonzero degree belong to a single connected component.
A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component
Strongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....

. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

s and all of its vertices with nonzero degree belong to a single strongly connected component.
A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph.

Fleury's algorithm

Fleury's algorithm is an elegant but inefficient algorithm which dates to 1883. Consider a graph known to have all edges in the same component and at most two vertices of odd degree. We start with a vertex of odd degree—if the graph has none, then start with any vertex. At each step we move across an edge whose deletion would not disconnect the graph, unless we have no choice, then we delete that edge. At the end of the algorithm there are no edges left, and the sequence of edges we moved across forms a Eulerian cycle if the graph has no vertices of odd degree; or a Eulerian trail if there are exactly two vertices of odd degree.

While the graph traversal in Fleury's algorithm is linear in the number of edges i.e.

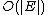, we also need to factor in the complexity of detecting bridges. If we are to re-run Tarjan

Robert Tarjan

Robert Endre Tarjan is a renowned American computer scientist. He is the discoverer of several important graph algorithms, including Tarjan's off-line least common ancestors algorithm, and co-inventor of both splay trees and Fibonacci heaps. Tarjan is currently the James S...

's linear time bridge finding algorithm

Bridge (graph theory)

In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....

after the removal of every edge, Fleury's algorithm will have a time complexity of

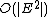A dynamic bridge-finding algorithm of allows this to be improved to

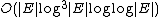, but this is still significantly slower than alternative algorithms.

Hierholzer's algorithm

Hierholzer's 1873 paper provides a different method for finding Euler cycles that is more efficient than Fleury's algorithm:

Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
As long as there exists a vertex v that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from v, following unused edges until returning to v, and join the tour formed in this way to the previous tour.

By using a data structure such as a doubly linked list to maintain the set of unused edges incident to each vertex, to maintain the list of vertices on the current tour that have unused edges, and to maintain the tour itself, the individual operations of the algorithm (finding unused edges exiting each vertex, finding a new starting vertex for a tour, and connecting two tours that share a vertex) may be performed in constant time each, so the overall algorithm takes linear time.

Complexity issues

The number of Eulerian circuits in digraphs can be calculated using the so-called BEST theorem
BEST theorem
In graph theory, a part of discrete mathematics, the BEST theorem gives a product formula for the number of Eulerian circuits in directed graphs. The name is an acronym of the names of people who discovered it: de Bruijn, van Aardenne-Ehrenfest, Smith and Tutte.- Precise statement :Let...

, named after de Bruijn, van Aardenne-Ehrenfest

Tatyana Pavlovna Ehrenfest

Tatyana Pavlovna Ehrenfest, later van Aardenne-Ehrenfest, was a Dutch mathematician. She was the daughter of Paul Ehrenfest and Tatyana Alexeyevna Afanasyeva .Tatyana Ehrenfest was born in Vienna, and spent her childhood in St Petersburg...

, Smith and Tutte

W. T. Tutte

William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...

. The formula states that the number of Eulerian circuits in a digraph is the product of certain degree factorials and the number of rooted arborescences

Arborescence (graph theory)

In graph theory, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v....

. The latter can be computed as a determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

, by the matrix tree theorem, giving a polynomial time algorithm.

BEST theorem is first stated in this form in a "note added in proof" to the Aardenne-Ehrenfest and de Bruijn paper (1951). The original proof was bijective

Bijective proof

In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...

and generalized the de Bruijn sequence

De Bruijn sequence

In combinatorial mathematics, a k-ary De Bruijn sequence B of order n, named after the Dutch mathematician Nicolaas Govert de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly...

s. It is a variation on an earlier result by Smith and Tutte (1941).

Counting the number of Eulerian circuits on undirected graphs is much more difficult. This problem is known to be #P

Sharp-P

In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...

-complete. In a positive direction, a Markov chain Monte Carlo

Markov chain Monte Carlo

Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...

approach, via the Kotzig transformations (introduced by Anton Kotzig

Anton Kotzig

Anton Kotzig was a Slovak–Canadian mathematician, expert in statistics, combinatorics and graph theory. The Ringel-Kotzig conjecture on graceful labeling of trees is named after him and Gerhard Ringel.- Biography :...

in 1968) is believed to give a sharp approximation for the number of Eulerian circuits in a graph.

Special cases

The asymptotic formula

Asymptotic analysis

In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...

for the number of Eulerian circuits in the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

s was determined by McKay

Brendan McKay

Brendan Damien McKay is a Professor in the Research School of Computer Science at the Australian National University . He has published extensively in combinatorics....

and Robinson (1995):

A similar formula was later obtained by M.I. Isaev (2009) for complete bipartite graph

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

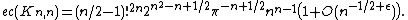
Applications

Eulerian trails are being used in bioinformatics

Bioinformatics

Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...

to reconstruct the DNA sequence

DNA sequence

The sequence or primary structure of a nucleic acid is the composition of atoms that make up the nucleic acid and the chemical bonds that bond those atoms. Because nucleic acids, such as DNA and RNA, are unbranched polymers, this specification is equivalent to specifying the sequence of...

from its fragments.

External links

Discussion of early mentions of Fleury's algorithm

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.