For other meanings of neighbourhoods in mathematics, see Neighbourhood (mathematics)

Neighbourhood (mathematics)

In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...

. For non-mathematical neighbourhoods, see Neighbourhood (disambiguation)

Neighbourhood (disambiguation)

A neighbourhood is a part of a city or town.Neighbourhood may also refer to:-Mathematics:*Neighbourhood , a concept in topology*Neighbourhood , a grouping in graph theory...

.

In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, an adjacent vertex of a vertex

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 v in a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

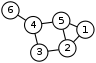
 is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a graph of 6 vertices and 7 edges. Vertex 5 is adjacent to vertices 1, 2, and 4 but it is not adjacent to 3 and 6. The neighbourhood of vertex 5 is the graph with three vertices, 1, 2, and 4, and one edge connecting vertices 1 and 2.

The neighbourhood is often denoted N_G(v) or (when the graph is unambiguous) N(v). The same neighbourhood notation may also be used to refer to sets of adjacent vertices rather than the corresponding induced subgraphs. The neighbourhood described above does not include v itself, and is more specifically the open neighbourhood of v; it is also possible to define a neighbourhood in which v itself is included, called the closed neighbourhood and denoted by N_G[v]. When stated without any qualification, a neighbourhood is assumed to be open.

Neighbourhoods may be used to represent graphs in computer algorithms, via the adjacency list

Adjacency list

In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...

 and adjacency matrix

Adjacency matrix

In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

 representations. Neighbourhoods are also used in the clustering coefficient

Clustering coefficient

In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...

 of a graph, which is a measure of the average density

Dense graph

In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...

 of its neighbourhoods. In addition, many important classes of graphs may be defined by properties of their neighbourhoods, or by symmetries that relate neighbourhoods to each other.

An isolated vertex has no adjacent vertices. The degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

 of a vertex is equal to the number of adjacent vertices. A special case is a loop

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

 that connects a vertex to itself; if such an edge exists, the vertex belongs to its own neighbourhood.

Local properties in graphs

If all vertices in G have neighbourhoods that are isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

 to the same graph H, G is said to be locally H, and if all vertices in G have neighbourhoods that belong to some graph family F, G is said to be locally F . For instance, in the octahedron graph

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

 shown in the figure, each vertex has a neighbourhood isomorphic to a cycle

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

 of four vertices, so the octahedron is locally C₄.

For example:

• Any complete graph
  Complete graph
  In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
  
   K_n is locally K_n-1. The only graphs that are locally complete are disjoint unions of complete graphs.
• A Turán graph
  Turán graph
  The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
  
   T(rs,r) is locally T((r-1)s,r-1). More generally any Turán graph is locally Turán.
• Every planar graph
  Planar graph
  In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
  
   is locally outerplanar
  Outerplanar graph
  In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
  
  . However, not every locally outerplanar graph is planar.
• A graph is triangle-free
  Triangle-free graph
  In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
  
   if and only if it is locally independent
  Independent set (graph theory)
  In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
  
  .
• Every k-chromatic graph is locally (k-1)-chromatic. Every locally k-chromatic graph has chromatic number .
• If a graph family F is closed under the operation of taking induced subgraphs, then every graph in F is also locally F. For instance, every chordal graph
  Chordal graph
  In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
  
   is locally chordal; every perfect graph
  Perfect graph
  In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
  
   is locally perfect; every comparability graph
  Comparability graph
  In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
  
   is locally comparable.
• A graph is locally cyclic if every neighbourhood is a cycle
  Cycle graph
  In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
  
  . For instance, the octahedron
  Octahedron
  In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
  
   is the unique locally C₄ graph, the icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
   is the unique locally C₅ graph, and the Paley graph
  Paley graph
  In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
  
   of order 13 is locally C₆. Locally cyclic graphs other than K₄ are exactly the underlying graphs of Whitney triangulations
  Triangulation (topology)
  In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
  
  , embeddings of graphs on surfaces in such a way that the faces of the embedding are the cliques of the graph . Locally cyclic graphs can have as many as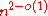 edges .
• Claw-free graphs are the graphs that are locally co-triangle-free
  Triangle-free graph
  In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
  
  ; that is, for all vertices, the complement graph
  Complement graph
  In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
  
   of the neighborhood of the vertex does not contain a triangle. A graph that is locally H is claw-free if and only if the independence number of H is at most two; for instance, the graph of the regular icosahedron is claw-free because it is locally C₅ and C₅ has independence number two.

Neighbourhood of a Set

For a set A of vertices, the neighbourhood of A is the union of the neighbourhoods of the vertices, and so it is the set of all vertices adjacent to at least one member of A.

A set A of vertices in a graph is said to be a module if every vertex in A has the same set of neighbors outside of A. Any graph has a uniquely recursive decomposition into modules, its modular decomposition

Modular decomposition

In graph theory, the modular decomposition is a decomposition of an undirected graph into subsets of vertices called modules. A module is a generalization of a connected component of a graph. Unlike connected components, however, one module can be a proper subset of another...

, which can be constructed from the graph in linear time; modular decomposition algorithms have applications in other graph algorithms including the recognition of comparability graph

Comparability graph

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...

s.