
Bridge (graph theory)
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
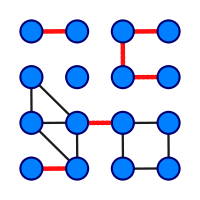
, a bridge (also known as a cut-edge or cut arc or an isthmus) is an edge whose deletion increases the number of connected components
Connected component (graph theory)
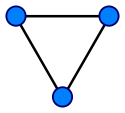
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
. Equivalently, an edge is a bridge if and only if it is not contained in any cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
.
A graph is said to be bridgeless if it contains no bridges. It is easy to see that this is equivalent to 2-edge-connectivity
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
of each nontrivial component.
A graph with
 nodes can contain at most
nodes can contain at most 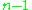 bridges, since adding additional edges must create a cycle.
bridges, since adding additional edges must create a cycle.Cycle double cover conjecture
An important open problem involving bridges is the cycle double cover conjecture, due to Seymour and SzekeresGeorge Szekeres
George Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
(1978 and 1979, independently), which states that every bridgeless graph admits a set of cycles which contains each edge exactly twice.
Bridge-Finding Algorithm
An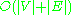 algorithm for finding bridges in a connected graph was found by Tarjan in 1974. A distributed version of the algorithm also exists.
algorithm for finding bridges in a connected graph was found by Tarjan in 1974. A distributed version of the algorithm also exists.Algorithm:
- Find a spanning treeSpanning treeSpanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
of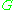
- Create a rooted tree
 from the spanning tree
from the spanning tree - Traverse the tree
 in preorderTree traversalIn computer science, tree-traversal refers to the process of visiting each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited...
in preorderTree traversalIn computer science, tree-traversal refers to the process of visiting each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited...
and number the nodes. Parent nodes in the tree now have lower numbers than child nodes. - For each node from
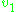 (the leaf nodes of the tree) to 1 (the root node of the tree) do:
(the leaf nodes of the tree) to 1 (the root node of the tree) do:
- Compute the number of descendants
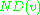 for this node.
for this node. - Compute
 and
and 
- For each
 such that
such that 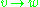 : if
: if 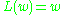 and
and 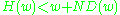 then
then 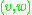 is a bridge.
is a bridge.
- Compute the number of descendants
Definitions:
A non-tree (undirected) edge between
 and
and  is denoted by
is denoted by 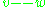 . An in-tree edge with
. An in-tree edge with  as the parent is denoted by
as the parent is denoted by 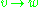 .
.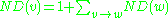 where
where  is the parent node of
is the parent node of  .
.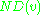 is the number of descendants of v (including itself) in the rooted spanning tree.
is the number of descendants of v (including itself) in the rooted spanning tree.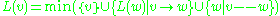
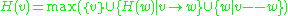
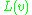 and
and 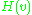 are the labels of the nodes with lowest and highest preorder label respectively reachable from v by travelling in the subtree rooted at v, along with at most one non-tree edge.
are the labels of the nodes with lowest and highest preorder label respectively reachable from v by travelling in the subtree rooted at v, along with at most one non-tree edge.This algorithm works because
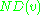 ,
, 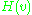 and
and 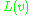 can all be computed for a node v provided we know their values on all in-tree descendants of v. Also, if and only if the edge
can all be computed for a node v provided we know their values on all in-tree descendants of v. Also, if and only if the edge 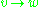 is a bridge, then it is clear that in the subtree rooted at
is a bridge, then it is clear that in the subtree rooted at  , it must be impossible to reach any node that is not a descendant of w. This is easy to check because the subtree rooted at w (that is, all descendants of w) consists of the nodes
, it must be impossible to reach any node that is not a descendant of w. This is easy to check because the subtree rooted at w (that is, all descendants of w) consists of the nodes 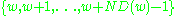 so we can
so we cansimply check if
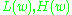 are in this set or not to check whether an edge is a bridge.
are in this set or not to check whether an edge is a bridge.Cut arc in trees
An edge or arc e = uv of a tree G is a cut arc of G if and only if the degree of the vertices u and v are greater than 1.Cut arcs are also defined for directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s

