Constructive proof
Encyclopedia
In mathematics
, a constructive proof is a method of proof
that demonstrates the existence of a mathematical object
with certain properties by creating or providing a method for creating such an object. This is in contrast to a nonconstructive proof (also known as an existence proof or pure existence theorem
) which proves the existence of a mathematical object with certain properties, but does not provide a means of constructing an example.
Many nonconstructive proofs assume the non-existence of the thing whose existence is required to be proven, and deduce a contradiction. The non-existence of the thing has therefore been shown to be logically impossible, and yet an actual example of the thing has not been found. Nearly every proof which invokes the axiom of choice is nonconstructive in nature because this axiom is fundamentally nonconstructive. The same can be said for proofs invoking König's lemma
.
Constructivism
is the philosophy that rejects all but constructive proofs in mathematics. Typically, supporters of this view deny that pure existence can be usefully characterized as "existence" at all: accordingly, a non-constructive proof is instead seen as "refuting the impossibility" of a mathematical object's existence, a strictly weaker statement.
Constructive proofs can be seen as defining certified mathematical algorithm
s: this idea is explored in the Brouwer–Heyting–Kolmogorov interpretation of constructive logic, the Curry–Howard correspondence between proofs and programs, and such logical systems as Per Martin-Löf
's Intuitionistic Type Theory
, and Thierry Coquand
and Gérard Huet
's Calculus of Constructions
.
s
and 
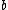such that 
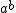is rational
." This theorem can be proved via a constructive proof, or via a non-constructive proof.
Jarden's non-constructive proof proceeds as follows:
This proof is non-constructive because it relies on the statement "Either q is rational or it is irrational" — an instance of the law of excluded middle
, which is not valid within a constructive proof. The non-constructive proof does not construct an example a and b; it merely gives a number of possibilities (in this case, two mutually exclusive possibilities) and shows that one of them — but does not show which one — must yield the desired example.
(It turns out that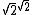
is irrational because of the Gelfond–Schneider theorem
, but this fact is irrelevant to the correctness of the non-constructive proof.)
A constructive proof of the theorem would give an actual example, such as: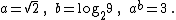
The square root of 2
is irrational, and 3 is rational.
is also irrational: if it were equal to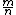 
, then, by the properties of logarithms, 9n would be equal to 2m, but the former is odd, and the latter is even.
A more substantial example is the graph minor theorem. A consequence of this theorem is that a graph
can be drawn on the torus
if, and only if, none of its minors
belong to a certain finite set of "forbidden minors". However, the proof of the existence of this finite set is not constructive, and the forbidden minors are not actually specified. They are still unknown.
, as in classical mathematics. However, it is also possible to give a Brouwerian counterexample to show that the statement is essentially non-constructive. This sort of counterexample shows that the statement implies some principle that is known to be non-constructive. For example, a particular statement may be shown to imply the law of the excluded middle. If it can be proved constructively that a statement implies some principle that is not constructively provable, then the statement itself cannot be constructively provable. An example of a Brouwerian counterexample is Diaconescu's theorem
showing that the full axiom of choice is non-constructive since it implies the law of excluded middle. A weak Brouwerian counterexample does not disprove a statement, however; it only shows that the statement has no constructive proof.
On the other hand Brouwer gives strong counterexamples, based on properties that hold only in his constructive mathematics. He uses strong counterexamples to show that the law of the excluded middle cannot hold. One of these properties is that two rational numbers can only be proved to be the same if every digit in the decimal expansion can be proved to be the same. If we define a decimal expansion such that some digit is dependent on some yet unsolved mathematical problem, we know beforehand that we cannot tell if this number is the same as some other decimal expansion which is independent of this problem. If the law of the excluded middle would hold - if we could say whether or not the two numbers are the same, that would mean we could solve the yet unsolved problem, which is not the case, so we have disproved the law of the excluded middle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a constructive proof is a method of proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that demonstrates the existence of a mathematical object
Mathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
with certain properties by creating or providing a method for creating such an object. This is in contrast to a nonconstructive proof (also known as an existence proof or pure existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
) which proves the existence of a mathematical object with certain properties, but does not provide a means of constructing an example.
Many nonconstructive proofs assume the non-existence of the thing whose existence is required to be proven, and deduce a contradiction. The non-existence of the thing has therefore been shown to be logically impossible, and yet an actual example of the thing has not been found. Nearly every proof which invokes the axiom of choice is nonconstructive in nature because this axiom is fundamentally nonconstructive. The same can be said for proofs invoking König's lemma
König's lemma
König's lemma or König's infinity lemma is a theorem in graph theory due to Dénes Kőnig . It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic,...
.
Constructivism
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
is the philosophy that rejects all but constructive proofs in mathematics. Typically, supporters of this view deny that pure existence can be usefully characterized as "existence" at all: accordingly, a non-constructive proof is instead seen as "refuting the impossibility" of a mathematical object's existence, a strictly weaker statement.
Constructive proofs can be seen as defining certified mathematical algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s: this idea is explored in the Brouwer–Heyting–Kolmogorov interpretation of constructive logic, the Curry–Howard correspondence between proofs and programs, and such logical systems as Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
's Intuitionistic Type Theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
, and Thierry Coquand
Thierry Coquand
Thierry Coquand is a professor in computer science at the University of Gothenburg, Sweden. He is known for his work in constructive mathematics, especially the calculus of constructions. He received his Ph.D. under the supervision of Gérard Huet.- External links :*...
and Gérard Huet
Gérard Huet
Gérard Pierre Huet is a French computer scientist.- Biography :Gérard Huet graduated from the Université Denis Diderot , Case Western Reserve University, and the Université de Paris....
's Calculus of Constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
.
Example
Consider the theorem "There exist irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s
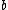and such that 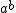is rationalRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
." This theorem can be proved via a constructive proof, or via a non-constructive proof.
Jarden's non-constructive proof proceeds as follows:
- Recall that
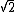is irrational, and 2 is rational. Consider the number 
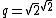. Either it is rational or it is irrational.
- If
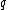is rational, then the theorem is true, with 
and 
both being 
.
- If
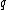is irrational, then the theorem is true, with 
being 
and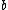 
being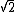 
, since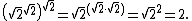
This proof is non-constructive because it relies on the statement "Either q is rational or it is irrational" — an instance of the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
, which is not valid within a constructive proof. The non-constructive proof does not construct an example a and b; it merely gives a number of possibilities (in this case, two mutually exclusive possibilities) and shows that one of them — but does not show which one — must yield the desired example.
(It turns out that
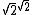is irrational because of the Gelfond–Schneider theoremGelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
, but this fact is irrelevant to the correctness of the non-constructive proof.)
A constructive proof of the theorem would give an actual example, such as:
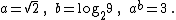
The square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is irrational, and 3 is rational.
is also irrational: if it were equal to 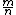, then, by the properties of logarithms, 9n would be equal to 2m, but the former is odd, and the latter is even.A more substantial example is the graph minor theorem. A consequence of this theorem is that a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
can be drawn on the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
if, and only if, none of its minors
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
belong to a certain finite set of "forbidden minors". However, the proof of the existence of this finite set is not constructive, and the forbidden minors are not actually specified. They are still unknown.
Brouwerian counterexamples
In constructive mathematics, a statement may be disproved by giving a counterexampleCounterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
, as in classical mathematics. However, it is also possible to give a Brouwerian counterexample to show that the statement is essentially non-constructive. This sort of counterexample shows that the statement implies some principle that is known to be non-constructive. For example, a particular statement may be shown to imply the law of the excluded middle. If it can be proved constructively that a statement implies some principle that is not constructively provable, then the statement itself cannot be constructively provable. An example of a Brouwerian counterexample is Diaconescu's theorem
Diaconescu's theorem
In mathematical logic, Diaconescu's theorem, or the Goodman–Myhill theorem, states that the full axiom of choice is sufficient to derive the law of the excluded middle, or restricted forms of it, in constructive set theory...
showing that the full axiom of choice is non-constructive since it implies the law of excluded middle. A weak Brouwerian counterexample does not disprove a statement, however; it only shows that the statement has no constructive proof.
On the other hand Brouwer gives strong counterexamples, based on properties that hold only in his constructive mathematics. He uses strong counterexamples to show that the law of the excluded middle cannot hold. One of these properties is that two rational numbers can only be proved to be the same if every digit in the decimal expansion can be proved to be the same. If we define a decimal expansion such that some digit is dependent on some yet unsolved mathematical problem, we know beforehand that we cannot tell if this number is the same as some other decimal expansion which is independent of this problem. If the law of the excluded middle would hold - if we could say whether or not the two numbers are the same, that would mean we could solve the yet unsolved problem, which is not the case, so we have disproved the law of the excluded middle.
Further reading
- J. FranklinJames Franklin (philosopher)James Franklin is an Australian philosopher, mathematician and historian of ideas. He was educated at St. Joseph's College, Hunters Hill, New South Wales. His undergraduate work was at the University of Sydney , where he attended St John's College and he was influenced by philosophers David Stove...
and A. Daoud (2011) Proof in Mathematics: An Introduction. Kew Books, ISBN 0646545094, ch. 4 - Hardy, G.H. & Wright, E.M.E. M. WrightSir Edward Maitland Wright was an English mathematician.He is best known for co-authoring “Hardy and Wright”, An Introduction to the Theory of Numbers, with G. H...
(1979) An Introduction to the Theory of Numbers (Fifth Edition). Oxford University Press. ISBN 0-19-853171-0 - Anne Sjerp Troelstra and Dirk van DalenDirk van DalenDirk van Dalen is a Dutch mathematician and historian of science.Van Dalen studied mathematics and physics and astronomy at the University of Amsterdam. Inspired by the work of LEJ Brouwer and Arend Heyting, he received his Ph.D...
(1988) "Constructivism in Mathematics: Volume 1" Elsevier Science. ISBN 978-0444705068