Hyperbolic motion
Encyclopedia
In geometry
, hyperbolic motions are isometric
automorphism
s of a hyperbolic space
. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein
in his Erlangen program
. The idea of reducing geometry to its characteristic group was developed particularly by Mario Pieri
in his reduction of the primitive notion
s of geometry to merely point
and motion.
Hyperbolic motions are in fact taken from inversive geometry: these are mappings composed of reflections in a line or a circle (or in a hyperplane
or a hypersphere
for hyperbolic spaces of more than two dimensions). To distinguish the hyperbolic motions, a particular line or circle is taken as the absolute. The proviso is that the absolute must be an invariant set of all hyperbolic motions. The absolute divides the plane into two connected component
s, and hyperbolic motions must not permute these components.
One of the most prevalent contexts for inversive geometry and hyperbolic motions is in the study of mappings of the complex plane
by Mobius transformations. Textbooks on complex functions often mention two common models of hyperbolic geometry: the Poincaré half-plane model
where the absolute is the real line on the complex plane, and the Poincaré disk model
where the absolute is the unit circle
in the complex plane.
This article exhibits these examples of the use of hyperbolic motions: the extension of the metric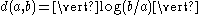
to the half-plane, and in the location of a quasi-sphere of a hypercomplex number system.
The points of the upper half-plane model HP are given in Cartesian coordinates as {(x,y): y > 0} or in polar coordinates as {(r cos a, r sin a): 0 < a < π, r > 0 }.The hyperbolic motions will be taken to be a composition
of three fundamental hyperbolic motions.
Let p = (x,y) or p = (r cos a, r sin a), p ∈ HP. The fundamental motions are:
Note: the shift and dilation are mappings from inversive geometry composed of a pair of reflections in vertical lines or concentric circles respectively.
). Set r = sec a and apply the third fundamental hyperbolic motion to obtain q = (r cos a, r sin a) where r = sec−1a = cos a. Now
so that q lies on the semicircle Z of radius ½ and center (½, 0). Thus the tangent ray at (1, 0) gets mapped to Z by the third fundamental hyperbolic motion. Any semicircle can be re-sized by a dilation to radius ½ and shifted to Z, then the inversion carries it to the tangent ray. So the collection of hyperbolic motions permutes the semicircles with diameters on y = 0 sometimes with vertical rays, and vice versa. Suppose one agrees to measure length on vertical rays by using the logarithm
function:
Then by means of hyperbolic motions one can measure distances between points on semicircles too: first move the points to Z with appropriate shift and dilation, then place them by inversion on the tangent ray where the logarithmic distance is known.
For m and n in HP, let b be the perpendicular bisector of the line segment connecting m and n. If b is parallel to the abscissa
, then m and n are connected by a vertical ray, otherwise b intersects the abscissa so there is a semicircle centered at this intersection that passes through m and n. The set HP becomes a metric space
when equipped with the distance d(m,n) for m,n ∈ HP as found on the vertical ray or semicircle. One calls the vertical rays and semicircles the hyperbolic lines in HP.
The geometry of points and hyperbolic lines in HP is an example of a non-Euclidean geometry
; nevertheless, the construction of the line and distance concepts for HP relies heavily on the original geometry of Euclid.
C. The geometric plane of Lobachevsky can be displayed in D with circular arcs perpendicular to the boundary of D signifying hyperbolic lines. Using the arithmetic and geometry of complex numbers, and Mobius transformations, there is the Poincaré disc model of the hyperbolic plane:
Suppose a and b are complex numbers with a a* − b b* = 1. Note that
so that |z| < 1 implies |(az + b*)/(bz + a*)| < 1 . Hence the disk D is an invariant set of the Möbius transformation
Since it also permutes the hyperbolic lines, we see that these transformations are motions of the D model of hyperbolic geometry
. A complex matrix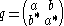
with aa* − bb* = 1, which represents the Möbius transformation from the projective viewpoint, can be considered to be on the unit quasi-sphere in the ring
of coquaternion
s.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, hyperbolic motions are isometric
Isometric
The term isometric comes from the Greek for "having equal measurement".isometric may mean:* Isometric projection , a method for the visual representation of three-dimensional objects in two dimensions; a form of orthographic projection, or more specifically, an axonometric projection.* Isometry and...
automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of a hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
in his Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
. The idea of reducing geometry to its characteristic group was developed particularly by Mario Pieri
Mario Pieri
Mario Pieri was an Italian mathematician who is known for his work on foundations of geometry.Pieri was born in Lucca, Italy, the son of Pellegrino Pieri and Ermina Luporini. Pellegrino was a lawyer. Pieri began his higher education at University of Bologna where he drew the attention of Salvatore...
in his reduction of the primitive notion
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
s of geometry to merely point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
and motion.
Hyperbolic motions are in fact taken from inversive geometry: these are mappings composed of reflections in a line or a circle (or in a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
or a hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
for hyperbolic spaces of more than two dimensions). To distinguish the hyperbolic motions, a particular line or circle is taken as the absolute. The proviso is that the absolute must be an invariant set of all hyperbolic motions. The absolute divides the plane into two connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s, and hyperbolic motions must not permute these components.
One of the most prevalent contexts for inversive geometry and hyperbolic motions is in the study of mappings of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
by Mobius transformations. Textbooks on complex functions often mention two common models of hyperbolic geometry: the Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
where the absolute is the real line on the complex plane, and the Poincaré disk model
Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
where the absolute is the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex plane.
This article exhibits these examples of the use of hyperbolic motions: the extension of the metric
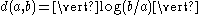to the half-plane, and in the location of a quasi-sphere of a hypercomplex number system.Introduction of metric in upper half-plane
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of three fundamental hyperbolic motions.
Let p = (x,y) or p = (r cos a, r sin a), p ∈ HP. The fundamental motions are:
- p → q = (x + c, y ), c ∈ R (left or right shift)
- p → q = (sx, sy ), s > 0 (dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
) - p → q = ( r −1 cos a, r −1 sin a ) (inversion in unit semicircle).
Note: the shift and dilation are mappings from inversive geometry composed of a pair of reflections in vertical lines or concentric circles respectively.
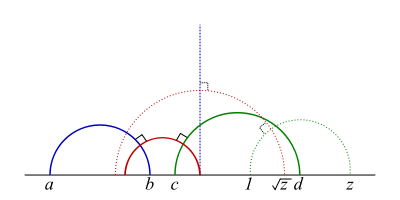
Use of semi-circle Z
Consider the triangle {(0,0),(1,0),(1,tan a)}. Since 1 + tan2a = sec2a, the length of the triangle hypotenuse is sec a (see secantSecant
Secant is a term in mathematics. It comes from the Latin secare . It can refer to:* a secant line, in geometry* the secant variety, in algebraic geometry...
). Set r = sec a and apply the third fundamental hyperbolic motion to obtain q = (r cos a, r sin a) where r = sec−1a = cos a. Now
- |q – (½, 0)|2 = (cos2a – ½)2 +cos2a sin2a = ¼
so that q lies on the semicircle Z of radius ½ and center (½, 0). Thus the tangent ray at (1, 0) gets mapped to Z by the third fundamental hyperbolic motion. Any semicircle can be re-sized by a dilation to radius ½ and shifted to Z, then the inversion carries it to the tangent ray. So the collection of hyperbolic motions permutes the semicircles with diameters on y = 0 sometimes with vertical rays, and vice versa. Suppose one agrees to measure length on vertical rays by using the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
function:
- d((x,y),(x,z)) = |log(z/y)|.
Then by means of hyperbolic motions one can measure distances between points on semicircles too: first move the points to Z with appropriate shift and dilation, then place them by inversion on the tangent ray where the logarithmic distance is known.
For m and n in HP, let b be the perpendicular bisector of the line segment connecting m and n. If b is parallel to the abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
, then m and n are connected by a vertical ray, otherwise b intersects the abscissa so there is a semicircle centered at this intersection that passes through m and n. The set HP becomes a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
when equipped with the distance d(m,n) for m,n ∈ HP as found on the vertical ray or semicircle. One calls the vertical rays and semicircles the hyperbolic lines in HP.
The geometry of points and hyperbolic lines in HP is an example of a non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
; nevertheless, the construction of the line and distance concepts for HP relies heavily on the original geometry of Euclid.
Disk model motions
Consider the disk D = {z ∈ C : z z* < 1 } in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C. The geometric plane of Lobachevsky can be displayed in D with circular arcs perpendicular to the boundary of D signifying hyperbolic lines. Using the arithmetic and geometry of complex numbers, and Mobius transformations, there is the Poincaré disc model of the hyperbolic plane:
Suppose a and b are complex numbers with a a* − b b* = 1. Note that
- |bz + a*|2 − |az + b*|2 = (aa* − bb*)(1 − |z|2),
so that |z| < 1 implies |(az + b*)/(bz + a*)| < 1 . Hence the disk D is an invariant set of the Möbius transformation
- f(z) = (az + b*)/(bz + a*).
Since it also permutes the hyperbolic lines, we see that these transformations are motions of the D model of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. A complex matrix
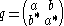
with aa* − bb* = 1, which represents the Möbius transformation from the projective viewpoint, can be considered to be on the unit quasi-sphere in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of coquaternion
Coquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s.