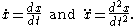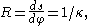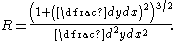Radius of curvature (mathematics)
Encyclopedia
In geometry
, the radius of curvature, R, of a curve at a point is a measure of the radius
of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise. It is given by
where s is the arc length from a fixed point on the curve, φ is the tangential angle
and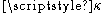 is the curvature.
is the curvature.
If the curve is given in Cartesian coordinates then the radius of curvature is (assuming it is differentiable up to degree 2):
If the curve is given parametrically
with parameter t then the radius of curvature is
where
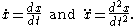
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the radius of curvature, R, of a curve at a point is a measure of the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise. It is given by
where s is the arc length from a fixed point on the curve, φ is the tangential angle
Tangential angle
In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent...
and
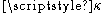 is the curvature.
is the curvature.If the curve is given in Cartesian coordinates then the radius of curvature is (assuming it is differentiable up to degree 2):
If the curve is given parametrically
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
with parameter t then the radius of curvature is
where