Dessin d'enfant
Encyclopedia
In mathematics
, a dessin d'enfant (French
for a "child's drawing", plural dessins d'enfants, "children's drawings") is a type of graph drawing
used to study Riemann surface
s and to provide combinatorial invariants
for the action of the absolute Galois group
of the rational number
s.
Intuitively, a dessin d'enfant is simply a graph, with its vertices
colored alternating black and white, embedded
onto an oriented surface
which in many cases is simply a plane
. In order for the coloring to exist, the graph must be bipartite
. The faces of the embedding must be topological disks. The surface and the embedding may be described combinatorially using a rotation system
, a cyclic order of the edges surrounding each vertex of the graph that describes the order in which the edges would be crossed by a path that travels clockwise on the surface in a small loop around the vertex. Any dessin can be used to provide the surface on which it is embedded with a structure as a Riemann surface. It natural to ask which Riemann surfaces arise in this way. The answer is provided by Belyi's theorem
, which states that these are precisely those which can be defined over the field of algebraic numbers (when considered as algebraic curves). The absolute Galois group transforms these particular curves into each other, and thereby also transforms the underlying dessins.
For a more detailed treatment of this subject, see or .
of William Rowan Hamilton
; in modern terms, Hamiltonian path
s on the icosahedral graph.
Recognizable modern dessins d'enfants (and Belyi functions) were used by Felix Klein
in , which he called Linienzüge (German, plural of Linienzug “line-track”, also used as a term for polygon
); he used a white circle for the preimage of 0 and a '+' for the preimage of 1, rather than a black circle for 0 and white circle for 1 as in modern notation. These diagrams were used in the construction of an 11-fold cover of the Riemann sphere by itself, with monodromy group PSL(2,11), and followed earlier work in (7-fold cover, PSL(2,7), connected to the Klein quartic
) and – these were all related to his investigations of the geometry of the quintic equation (and the group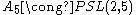
), collected in his famous 1884/88 Lectures on the Icosahedron.
These three surfaces form a "trinity" in the sense of Vladimir Arnold
, which can also be described as a McKay correspondence. In this collection, the projective special linear groups PSL(2,5), PSL(2,7), and PSL(2,11) (orders 60, 168, 660) are analogous, corresponding to icosahedral symmetry
(genus 0), the symmetries of the Klein quartic (genus 2), and the buckyball surface (genus 70). These are further connected to many other exceptional phenomena, which is elaborated at "trinities"; see surfaces related to the Klein quartic for further relations.
in 1984 in his Esquisse d'un Programme
. quotes Grothendieck regarding his discovery of the Galois action on dessins d'enfants:
The complex number
s, together with a special point designated as ∞, form a topological space
known as the Riemann sphere
. Any polynomial
, and more generally any rational function
p(x)/q(x) where p and q are polynomials, transforms the Riemann sphere by mapping it to itself.
Consider, for example, the rational function
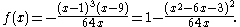
At most points of the Riemann sphere, this transformation is a local homeomorphism
: it maps a small disk centered at any point in a one-to-one way into another disk. However, at certain critical points
, the mapping is more complicated, and maps a disk centered at the point in a k-to-one way onto its image. The number k is known as the degree of the critical point and the transformed image of a critical point is known as a critical value
.
The example given above, ƒ, has the following critical points and critical values (some points of the Riemann sphere that, while not themselves critical, map to one of the critical values, are also included; these are indicated by having degree one):
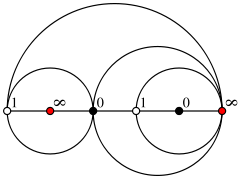
One may form a dessin d'enfant from ƒ by placing black points at the preimages of 0 (that is, at 1 and 9), white points at the preimages of 1 (that is, at 3 ± 2√3), and arcs at the preimages of the line segment
[0, 1]. This line segment has four preimages, two along the line segment from 1 to 9 and two forming a simple closed curve that loops from 1 to itself, surrounding 0; the resulting dessin is shown in the figure.
In the other direction, from this dessin, described as a combinatorial object without specifying the locations of the critical points, one may form a compact Riemann surface
, and a map from that surface to the Riemann sphere, equivalent to the map from which the dessin was originally constructed. To do so, place a point labeled ∞ within each region of the dessin (shown as the red points in the second figure), and triangulate
each region by connecting this point to the black and white points forming the boundary of the region, connecting multiple times to the same black or white point if it appears multiple times on the boundary of the region. Each triangle in the triangulation has three vertices labeled 0 (for the black points), 1 (for the white points), or ∞. For each triangle, substitute a half-plane, either the upper half-plane for a triangle that has 0, 1, and ∞ in counterclockwise order or the lower half-plane for a triangle that has them in clockwise order, and for every adjacent pair of triangles glue the corresponding half-planes together along the portion of their boundaries indicated by the vertex labels. The resulting Riemann surface can be mapped to the Riemann sphere by using the identity map within each half-plane. Thus, the dessin d'enfant formed from ƒ is sufficient to describe ƒ itself up to biholomorphism.
The same construction applies more generally when X is any Riemann surface and ƒ is a Belyi function
; that is, a holomorphic function
ƒ from X to the Riemann sphere having only 0, 1, and ∞ as critical values. A pair (X, ƒ) of this type is known as a Belyi pair. From any Belyi pair (X, ƒ) one can form a dessin d'enfant, drawn on the surface X, that has its black points at the preimages ƒ−1(0) of 0, its white points at the preimages ƒ−1(1) of 1, and its edges placed along the preimages ƒ−1([0, 1]) of the line segment [0, 1]. Conversely, any dessin d'enfant on any surface X can be used to define gluing instructions for a collection of halfspaces that together form a Riemann surface homeomorphic to X; mapping each halfspace by the identity to the Riemann sphere produces a Belyi function ƒ on X, and therefore leads to a Belyi pair (X, ƒ). Any two Belyi pairs (X, ƒ) that lead to combinatorially equivalent dessins d'enfants are biholomorphic, and Belyi's theorem
implies that, for any compact Riemann surface X defined over the algebraic number
s, there is a Belyi function ƒ and a dessin d'enfant that provides a combinatorial description of both X and ƒ.
The resulting triangulation is a triangulation by the reflection domains of a triangle group
; for genus greater than 1, the resulting triangle group is a (cocompact) Fuchsian group
(specifically, a Fuchsian triangle group) – discrete isometries of the hyperbolic plane, and the surface is the quotient of the hyperbolic plane by a finite index subgroup Γ in this group.
Conversely, given a Riemann surface that is a quotient of a (2,3,n) tiling, the associated dessin is the Cayley graph given by the order two and order three generators; equivalently, the 1-skeleton (vertices and edges) of the order-3 tiling by n-gons: vertices give black dots, centers of edges give white dots, and centers of faces give the points over infinity.
, the number of incident edges, that equals its degree as a critical point of the Belyi function. In the example above, all white points have degree two; dessins with the property that each white point has two edges are known as clean, and their corresponding Belyi functions are called pure. When this happens, one can describe the dessin by a simpler embedded graph, one that has only the black points as its vertices and that has an edge for each white point with endpoints at the white point's two black neighbors. For instance, the dessin shown in the figure could be drawn more simply in this way as a pair of black points with an edge between them and a self-loop on one of the points.
It is common to draw only the black points of a clean dessin and to leave the white points unmarked; one can recover the full dessin by adding a white point at the midpoint of each edge of the map.
Thus, any embedding of a graph on a surface in which each face is a disk (that is, a topological map) gives rise to a dessin by treating the graph vertices as black points of a dessin and placing white points at the midpoint of each embedded graph edge.
If a map corresponds to a Belyi function ƒ, its dual map
(the dessin formed from the preimages of the line segment [1, ∞]) corresponds to the multiplicative inverse
1/ƒ.
A dessin that is not clean can be transformed into a clean dessin on the same surface, by recoloring all of its points as black and adding new white points on each of its edges. The corresponding transformation of Belyi pairs is to replace a Belyi function β by the pure Belyi function γ = 4β(β − 1). One may calculate the critical points of γ directly from this formula: γ−1(0) = β−1(0) ∪ β−1(1), γ−1(∞) = β−1(∞), and γ−1(1) = β−1(1/2). Thus, γ−1(1) is the preimage under β of the midpoint of the line segment [0,1], and the edges of the dessin formed from γ subdivide
the edges of the dessin formed from β.
Under the interpretation of a clean dessin as a map, an arbitrary dessin is a hypermap: that is, a drawing of a hypergraph
in which the black points represent vertices and the white points represent hyperedges.
The simplest bipartite graphs are the trees
. Any embedding of a tree has a single region, and therefore by Euler's formula
lies on a spherical surface. The corresponding Belyi pair forms a transformation of the Riemann sphere which, if one places the pole at ∞, can be represented as a polynomial
. Conversely, any polynomial with 0 and 1 as its finite critical values forms a Belyi function from the Riemann sphere to itself, having a single infinite-valued critical point, and corresponding to a dessin d'enfant that is a tree. The degree of the polynomial equals the number of edges in the corresponding tree.
For example, take p to be the monomial
p(x) = xd having only one finite critical point and critical value, both zero. Although 1 is not a critical value for p, it is still possible to interpret p as a Belyi function from the Riemann sphere to itself because its critical values all lie in the set {0,1,∞}. The corresponding dessin d'enfant is a star
having one central black vertex connected to d white leaves (a complete bipartite graph
K1,d).
More generally, a polynomial p(x) having two critical values y1 and y2 is known as a Shabat polynomial, after George Shabat. Such a polynomial may be normalized into a Belyi function, with its critical values at 0 and 1, by the formula
but it may be more convenient to leave p in its un-normalized form.
An important family of examples of Shabat polynomials are given by the Chebyshev polynomials
of the first kind, Tn(x), which have −1 and 1 as critical values. The corresponding dessins take the form of path graph
s, alternating between black and white vertices, with n edges in the path. Due to the connection between Shabat polynomials and Chebyshev polynomials, Shabat polynomials themselves are sometimes called generalized Chebyshev polynomials.
Different trees will, in general, correspond to different Shabat polynomials, as will different embeddings or colorings of the same tree. Up to normalization and linear transformations of its argument, the Shabat polynomial is uniquely determined from a coloring of an embedded tree, but it is not always straightforward to find a Shabat polynomial that has a given embedded tree as its dessin d'enfant.
The polynomial
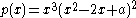
may be made into a Shabat polynomial by choosing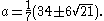
The two choices of a lead to two Belyi functions ƒ1 and ƒ2. These functions, though closely related to each other, are not equivalent, as they are described by the two nonisomorphic
trees shown in the figure.
However, as these polynomials are defined over the algebraic number field
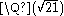, they may be transformed by the action
of the absolute Galois group
Γ of the rational numbers. An element of Γ that transforms √21 to −√21 will transform ƒ1 into ƒ2 and vice versa, and thus can also be said to transform each of the two trees shown in the figure into the other tree. More generally, due to the fact that the critical values of any Belyi function are the pure rationals 0, 1, and ∞, these critical values are unchanged by the Galois action, so this action takes Belyi pairs to other Belyi pairs. One may define an action of Γ on any dessin d'enfant by the corresponding action on Belyi pairs; this action, for instance, permutes
the two trees shown in the figure.
Due to Belyi's theorem, the action of Γ on dessins is faithful (that is, every two elements of Γ define different permutations on the set of dessins), so the study of dessins d'enfants can tell us much about Γ itself. In this light, it is of great interest to understand which dessins may be transformed into each other by the action of Γ and which may not. For instance, one may observe that the two trees shown have the same degree sequences for their black nodes and white nodes: both have a black node with degree three, two black nodes with degree two, two white nodes with degree two, and three white nodes with degree one. This equality is not a coincidence: whenever Γ transforms one dessin into another, both will have the same degree sequence. The degree sequence is one known invariant
of the Galois action, but not the only invariant.
The stabilizer of a dessin is the subgroup of Γ consisting of group elements that leave the dessin unchanged. Due to the Galois correspondence between subgroups of Γ and algebraic number fields, the stabilizer corresponds to a field, the field of moduli of the dessin. An orbit of a dessin is the set of all other dessins into which it may be transformed; due to the degree invariant, orbits are necessarily finite and stabilizers are of finite index
. One may similarly define the stabilizer of an orbit (the subgroup that fixes all elements of the orbit) and the corresponding field of moduli of the orbit, another invariant of the dessin. The stabilizer of the orbit is the maximal normal subgroup
of Γ contained in the stabilizer of the dessin, and the field of moduli of the orbit corresponds to the smallest normal extension of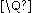
that contains the field of moduli of the dessin. For instance, for the two conjugate dessins considered in this section, the field of moduli of the orbit is 
. The two Belyi functions ƒ1 and ƒ2 of this example are defined over the field of moduli, but there exist dessins for which the field of definition of the Belyi function must be larger than the field of moduli.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dessin d'enfant (French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
for a "child's drawing", plural dessins d'enfants, "children's drawings") is a type of graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
used to study Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s and to provide combinatorial invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
for the action of the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s.
Intuitively, a dessin d'enfant is simply a graph, with its vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
colored alternating black and white, embedded
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
onto an oriented surface
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
which in many cases is simply a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. In order for the coloring to exist, the graph must be bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. The faces of the embedding must be topological disks. The surface and the embedding may be described combinatorially using a rotation system
Rotation system
In combinatorial mathematics, rotation systems encode embeddings of graphs onto orientable surfaces, by describing the circular ordering of a graph's edges around each vertex....
, a cyclic order of the edges surrounding each vertex of the graph that describes the order in which the edges would be crossed by a path that travels clockwise on the surface in a small loop around the vertex. Any dessin can be used to provide the surface on which it is embedded with a structure as a Riemann surface. It natural to ask which Riemann surfaces arise in this way. The answer is provided by Belyi's theorem
Belyi's theorem
In mathematics, Belyi's theorem on algebraic curves states that any non-singular algebraic curve C, defined by algebraic number coefficients, represents a compact Riemann surface which is a ramified covering of the Riemann sphere, ramified at three points only.It follows that the Riemann surface in...
, which states that these are precisely those which can be defined over the field of algebraic numbers (when considered as algebraic curves). The absolute Galois group transforms these particular curves into each other, and thereby also transforms the underlying dessins.
For a more detailed treatment of this subject, see or .
19th century
Early proto-forms of dessins d'enfants appeared as early as 1856 in the Icosian CalculusIcosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
of William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
; in modern terms, Hamiltonian path
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
s on the icosahedral graph.
Recognizable modern dessins d'enfants (and Belyi functions) were used by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
in , which he called Linienzüge (German, plural of Linienzug “line-track”, also used as a term for polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
); he used a white circle for the preimage of 0 and a '+' for the preimage of 1, rather than a black circle for 0 and white circle for 1 as in modern notation. These diagrams were used in the construction of an 11-fold cover of the Riemann sphere by itself, with monodromy group PSL(2,11), and followed earlier work in (7-fold cover, PSL(2,7), connected to the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
) and – these were all related to his investigations of the geometry of the quintic equation (and the group
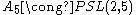), collected in his famous 1884/88 Lectures on the Icosahedron.These three surfaces form a "trinity" in the sense of Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, which can also be described as a McKay correspondence. In this collection, the projective special linear groups PSL(2,5), PSL(2,7), and PSL(2,11) (orders 60, 168, 660) are analogous, corresponding to icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(genus 0), the symmetries of the Klein quartic (genus 2), and the buckyball surface (genus 70). These are further connected to many other exceptional phenomena, which is elaborated at "trinities"; see surfaces related to the Klein quartic for further relations.
20th century
Dessins d'enfant in their modern form were then rediscovered over a century later and named by Alexander GrothendieckAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
in 1984 in his Esquisse d'un Programme
Esquisse d'un Programme
"Esquisse d'un Programme" is a famous proposal for long-term mathematical research made by the German-born, French mathematician Alexander Grothendieck...
. quotes Grothendieck regarding his discovery of the Galois action on dessins d'enfants:
Riemann surfaces and Belyi pairs
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, together with a special point designated as ∞, form a topological space
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
known as the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, and more generally any rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
p(x)/q(x) where p and q are polynomials, transforms the Riemann sphere by mapping it to itself.
Consider, for example, the rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
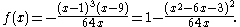
At most points of the Riemann sphere, this transformation is a local homeomorphism
Local homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
: it maps a small disk centered at any point in a one-to-one way into another disk. However, at certain critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
, the mapping is more complicated, and maps a disk centered at the point in a k-to-one way onto its image. The number k is known as the degree of the critical point and the transformed image of a critical point is known as a critical value
Critical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
.
The example given above, ƒ, has the following critical points and critical values (some points of the Riemann sphere that, while not themselves critical, map to one of the critical values, are also included; these are indicated by having degree one):
| critical point x | critical value ƒ(x) | degree |
|---|---|---|
| 0 | ∞ | 1 |
| 1 | 0 | 3 |
| 9 | 0 | 1 |
| 3 + 2√3 ≈ 6.464 | 1 | 2 |
| 3 − 2√3 ≈ −0.464 | 1 | 2 |
| ∞ | ∞ | 3 |
One may form a dessin d'enfant from ƒ by placing black points at the preimages of 0 (that is, at 1 and 9), white points at the preimages of 1 (that is, at 3 ± 2√3), and arcs at the preimages of the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
[0, 1]. This line segment has four preimages, two along the line segment from 1 to 9 and two forming a simple closed curve that loops from 1 to itself, surrounding 0; the resulting dessin is shown in the figure.
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
, and a map from that surface to the Riemann sphere, equivalent to the map from which the dessin was originally constructed. To do so, place a point labeled ∞ within each region of the dessin (shown as the red points in the second figure), and triangulate
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
each region by connecting this point to the black and white points forming the boundary of the region, connecting multiple times to the same black or white point if it appears multiple times on the boundary of the region. Each triangle in the triangulation has three vertices labeled 0 (for the black points), 1 (for the white points), or ∞. For each triangle, substitute a half-plane, either the upper half-plane for a triangle that has 0, 1, and ∞ in counterclockwise order or the lower half-plane for a triangle that has them in clockwise order, and for every adjacent pair of triangles glue the corresponding half-planes together along the portion of their boundaries indicated by the vertex labels. The resulting Riemann surface can be mapped to the Riemann sphere by using the identity map within each half-plane. Thus, the dessin d'enfant formed from ƒ is sufficient to describe ƒ itself up to biholomorphism.
The same construction applies more generally when X is any Riemann surface and ƒ is a Belyi function
Belyi's theorem
In mathematics, Belyi's theorem on algebraic curves states that any non-singular algebraic curve C, defined by algebraic number coefficients, represents a compact Riemann surface which is a ramified covering of the Riemann sphere, ramified at three points only.It follows that the Riemann surface in...
; that is, a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
ƒ from X to the Riemann sphere having only 0, 1, and ∞ as critical values. A pair (X, ƒ) of this type is known as a Belyi pair. From any Belyi pair (X, ƒ) one can form a dessin d'enfant, drawn on the surface X, that has its black points at the preimages ƒ−1(0) of 0, its white points at the preimages ƒ−1(1) of 1, and its edges placed along the preimages ƒ−1([0, 1]) of the line segment [0, 1]. Conversely, any dessin d'enfant on any surface X can be used to define gluing instructions for a collection of halfspaces that together form a Riemann surface homeomorphic to X; mapping each halfspace by the identity to the Riemann sphere produces a Belyi function ƒ on X, and therefore leads to a Belyi pair (X, ƒ). Any two Belyi pairs (X, ƒ) that lead to combinatorially equivalent dessins d'enfants are biholomorphic, and Belyi's theorem
Belyi's theorem
In mathematics, Belyi's theorem on algebraic curves states that any non-singular algebraic curve C, defined by algebraic number coefficients, represents a compact Riemann surface which is a ramified covering of the Riemann sphere, ramified at three points only.It follows that the Riemann surface in...
implies that, for any compact Riemann surface X defined over the algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, there is a Belyi function ƒ and a dessin d'enfant that provides a combinatorial description of both X and ƒ.
The resulting triangulation is a triangulation by the reflection domains of a triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
; for genus greater than 1, the resulting triangle group is a (cocompact) Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
(specifically, a Fuchsian triangle group) – discrete isometries of the hyperbolic plane, and the surface is the quotient of the hyperbolic plane by a finite index subgroup Γ in this group.
Conversely, given a Riemann surface that is a quotient of a (2,3,n) tiling, the associated dessin is the Cayley graph given by the order two and order three generators; equivalently, the 1-skeleton (vertices and edges) of the order-3 tiling by n-gons: vertices give black dots, centers of edges give white dots, and centers of faces give the points over infinity.
Maps and hypermaps
A vertex in a dessin has a graph-theoretic degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
, the number of incident edges, that equals its degree as a critical point of the Belyi function. In the example above, all white points have degree two; dessins with the property that each white point has two edges are known as clean, and their corresponding Belyi functions are called pure. When this happens, one can describe the dessin by a simpler embedded graph, one that has only the black points as its vertices and that has an edge for each white point with endpoints at the white point's two black neighbors. For instance, the dessin shown in the figure could be drawn more simply in this way as a pair of black points with an edge between them and a self-loop on one of the points.
It is common to draw only the black points of a clean dessin and to leave the white points unmarked; one can recover the full dessin by adding a white point at the midpoint of each edge of the map.
Thus, any embedding of a graph on a surface in which each face is a disk (that is, a topological map) gives rise to a dessin by treating the graph vertices as black points of a dessin and placing white points at the midpoint of each embedded graph edge.
If a map corresponds to a Belyi function ƒ, its dual map
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
(the dessin formed from the preimages of the line segment [1, ∞]) corresponds to the multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
1/ƒ.
A dessin that is not clean can be transformed into a clean dessin on the same surface, by recoloring all of its points as black and adding new white points on each of its edges. The corresponding transformation of Belyi pairs is to replace a Belyi function β by the pure Belyi function γ = 4β(β − 1). One may calculate the critical points of γ directly from this formula: γ−1(0) = β−1(0) ∪ β−1(1), γ−1(∞) = β−1(∞), and γ−1(1) = β−1(1/2). Thus, γ−1(1) is the preimage under β of the midpoint of the line segment [0,1], and the edges of the dessin formed from γ subdivide
Homeomorphism (graph theory)
In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
the edges of the dessin formed from β.
Under the interpretation of a clean dessin as a map, an arbitrary dessin is a hypermap: that is, a drawing of a hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
in which the black points represent vertices and the white points represent hyperedges.
Trees and Shabat polynomials
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
. Any embedding of a tree has a single region, and therefore by Euler's formula
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
lies on a spherical surface. The corresponding Belyi pair forms a transformation of the Riemann sphere which, if one places the pole at ∞, can be represented as a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
. Conversely, any polynomial with 0 and 1 as its finite critical values forms a Belyi function from the Riemann sphere to itself, having a single infinite-valued critical point, and corresponding to a dessin d'enfant that is a tree. The degree of the polynomial equals the number of edges in the corresponding tree.
For example, take p to be the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
p(x) = xd having only one finite critical point and critical value, both zero. Although 1 is not a critical value for p, it is still possible to interpret p as a Belyi function from the Riemann sphere to itself because its critical values all lie in the set {0,1,∞}. The corresponding dessin d'enfant is a star
Star (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
having one central black vertex connected to d white leaves (a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K1,d).
More generally, a polynomial p(x) having two critical values y1 and y2 is known as a Shabat polynomial, after George Shabat. Such a polynomial may be normalized into a Belyi function, with its critical values at 0 and 1, by the formula
but it may be more convenient to leave p in its un-normalized form.
An important family of examples of Shabat polynomials are given by the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the first kind, Tn(x), which have −1 and 1 as critical values. The corresponding dessins take the form of path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
s, alternating between black and white vertices, with n edges in the path. Due to the connection between Shabat polynomials and Chebyshev polynomials, Shabat polynomials themselves are sometimes called generalized Chebyshev polynomials.
Different trees will, in general, correspond to different Shabat polynomials, as will different embeddings or colorings of the same tree. Up to normalization and linear transformations of its argument, the Shabat polynomial is uniquely determined from a coloring of an embedded tree, but it is not always straightforward to find a Shabat polynomial that has a given embedded tree as its dessin d'enfant.
The absolute Galois group and its invariants
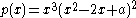
may be made into a Shabat polynomial by choosing
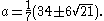
The two choices of a lead to two Belyi functions ƒ1 and ƒ2. These functions, though closely related to each other, are not equivalent, as they are described by the two nonisomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
trees shown in the figure.
However, as these polynomials are defined over the algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
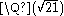, they may be transformed by the actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
Γ of the rational numbers. An element of Γ that transforms √21 to −√21 will transform ƒ1 into ƒ2 and vice versa, and thus can also be said to transform each of the two trees shown in the figure into the other tree. More generally, due to the fact that the critical values of any Belyi function are the pure rationals 0, 1, and ∞, these critical values are unchanged by the Galois action, so this action takes Belyi pairs to other Belyi pairs. One may define an action of Γ on any dessin d'enfant by the corresponding action on Belyi pairs; this action, for instance, permutes
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
the two trees shown in the figure.
Due to Belyi's theorem, the action of Γ on dessins is faithful (that is, every two elements of Γ define different permutations on the set of dessins), so the study of dessins d'enfants can tell us much about Γ itself. In this light, it is of great interest to understand which dessins may be transformed into each other by the action of Γ and which may not. For instance, one may observe that the two trees shown have the same degree sequences for their black nodes and white nodes: both have a black node with degree three, two black nodes with degree two, two white nodes with degree two, and three white nodes with degree one. This equality is not a coincidence: whenever Γ transforms one dessin into another, both will have the same degree sequence. The degree sequence is one known invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the Galois action, but not the only invariant.
The stabilizer of a dessin is the subgroup of Γ consisting of group elements that leave the dessin unchanged. Due to the Galois correspondence between subgroups of Γ and algebraic number fields, the stabilizer corresponds to a field, the field of moduli of the dessin. An orbit of a dessin is the set of all other dessins into which it may be transformed; due to the degree invariant, orbits are necessarily finite and stabilizers are of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
. One may similarly define the stabilizer of an orbit (the subgroup that fixes all elements of the orbit) and the corresponding field of moduli of the orbit, another invariant of the dessin. The stabilizer of the orbit is the maximal normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of Γ contained in the stabilizer of the dessin, and the field of moduli of the orbit corresponds to the smallest normal extension of
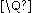that contains the field of moduli of the dessin. For instance, for the two conjugate dessins considered in this section, the field of moduli of the orbit is . The two Belyi functions ƒ1 and ƒ2 of this example are defined over the field of moduli, but there exist dessins for which the field of definition of the Belyi function must be larger than the field of moduli.