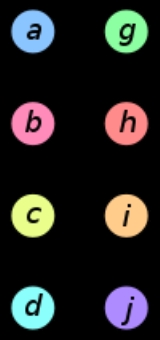
Graph isomorphism
Overview
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an isomorphism of graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s G and H is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the vertex sets of G and H
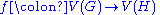
such that any two vertices u and v of G are adjacent
Adjacent
Adjacent is an adjective meaning contiguous, adjoining or abuttingIn geometry, adjacent is when sides meet to make an angle.In graph theory adjacent nodes in a graph are linked by an edge....
in G if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
ƒ(u) and ƒ(v) are adjacent in H. This kind of bijection is commonly called "edge-preserving bijection", in accordance with the general notion of isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
being a structure-preserving bijection.
In the above definition, graphs are understood to be undirected
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
non-labeled non-weighted graphs.

