.gif)
Homeomorphism (graph theory)
Encyclopedia
In graph theory
, two graphs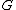
and 
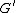are homeomorphic if there is an isomorphism
from some subdivision of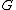
to some subdivision of 
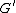. If the edges of a graph are thought of as lines drawn from one vertex to another (as they are usually depicted in illustrations), then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if they are homeomorphic
in the sense in which the term is used in topology
.
For example, the edge e, with endpoints {u,v}:
can be subdivided into two edges, e1 and e2, connecting to a new vertex w:
The reverse operation, smoothing out or smoothing a vertex w with regards to the pair of edges (e,f) incident on w, removes both edges containing w and replaces (e,f) with a new edge that connects the other endpoints of the pair. Here it is emphasized that only 2-valent vertices can be smoothed.
For example, the simple connected
graph with two edges, e1 {u,w} and e2 {w,v}:
has a vertex (namely w) that can be smoothed away, resulting in::
Determining whether for graphs G and H, H is homeomorphic to a subgraph of G, is an NP-complete
problem.
subdivides each edge of the graph. This is a special subdivision, as it always results in a bipartite graph
. This procedure can be repeated, so that the nth barycentric subdivision is the barycentric subdivision of the n-1th barycentric subdivision of the graph. The second such subdivision is always a simple graph.
In fact, a graph homeomorphic to K5 or K3,3 is called a Kuratowski subgraph.
A generalization, flowing from the Robertson–Seymour theorem
, asserts that for each integer g, there is a finite obstruction set of graphs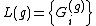
such that a graph H is embeddable on a surface of genus
g if and only if H contains no homeomorphic copy of any of the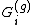
. For example, 
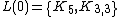contains the Kuratowski subgraphs.
G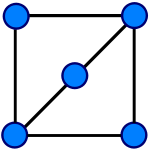
H 
If G' is the graph created by subdivision of the outer edges of G and H' is the graph created by subdivision of the inner edge of H, then G' and H' have a similar graph drawing:
G', H'
Therefore, there exists an isomorphism between G' and H', meaning G and H are homeomorphic.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, two graphs
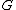and 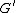are homeomorphic if there is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
from some subdivision of
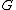to some subdivision of 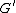. If the edges of a graph are thought of as lines drawn from one vertex to another (as they are usually depicted in illustrations), then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if they are homeomorphicHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
in the sense in which the term is used in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Subdivisions
In general, a subdivision of a graph G is a graph resulting from the subdivision of edges in G. The subdivision of some edge e with endpoints {u,v} yields a graph containing one new vertex w, and with an edge set replacing e by two new edges, {u,w} and {w,v}.For example, the edge e, with endpoints {u,v}:
 |
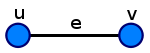can be subdivided into two edges, e1 and e2, connecting to a new vertex w:
 |
The reverse operation, smoothing out or smoothing a vertex w with regards to the pair of edges (e,f) incident on w, removes both edges containing w and replaces (e,f) with a new edge that connects the other endpoints of the pair. Here it is emphasized that only 2-valent vertices can be smoothed.
For example, the simple connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
graph with two edges, e1 {u,w} and e2 {w,v}:
|
has a vertex (namely w) that can be smoothed away, resulting in::
|
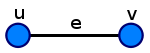Determining whether for graphs G and H, H is homeomorphic to a subgraph of G, is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem.
Barycentric Subdivisions
The barycentric subdivisionBarycentric subdivision
In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.The name...
subdivides each edge of the graph. This is a special subdivision, as it always results in a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. This procedure can be repeated, so that the nth barycentric subdivision is the barycentric subdivision of the n-1th barycentric subdivision of the graph. The second such subdivision is always a simple graph.
Embedding on a surface
It is evident that subdividing a graph preserves planarity. Kuratowski's theorem states that- a finite graph is planarPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it contains no subgraph homeomorphic to K5 (complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on five verticesVertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
) or K3,3 (complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
on six vertices, three of which connect to each of the other three).
In fact, a graph homeomorphic to K5 or K3,3 is called a Kuratowski subgraph.
A generalization, flowing from the Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
, asserts that for each integer g, there is a finite obstruction set of graphs
such that a graph H is embeddable on a surface of genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g if and only if H contains no homeomorphic copy of any of the
. For example, 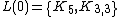contains the Kuratowski subgraphs.Example
In the following example, graph G and graph H are homeomorphic.G
G', H'