
Contact mechanics
Encyclopedia
Contact mechanics is the study of the deformation
of solids that touch each other at one or more points. The physical and mathematical formulation of the subject is built upon the mechanics of materials and continuum mechanics
and focuses on computations involving elastic
, viscoelastic
, and plastic bodies in static
or dynamic contact. Central aspects in contact mechanics are the pressure
s and adhesion
acting perpendicular to the contacting bodies' surfaces, the normal direction, and the friction
al stresses acting tangentially
between the surfaces. This page focuses mainly on the normal direction, i.e. on frictionless contact mechanics. Frictional contact mechanics
is discussed separately.
Contact mechanics is foundational to the field of mechanical engineering
; it provides necessary information for the safe and energy efficient design of technical systems and for the study of tribology
and indentation hardness
. Principles of contacts mechanics can be applied in areas such as locomotive wheel-rail contact, coupling
devices, braking
systems, tire
s, bearings
, combustion engines
, mechanical linkage
s, gasket
seals, metalworking
, metal forming, ultrasonic welding
, electrical contacts
, and many others. Current challenges faced in the field may include stress analysis
of contact and coupling members and the influence of lubrication
and material design
on friction
and wear
. Applications of contact mechanics further extend into the micro
- and nanotechnological
realm.
The original work in contact mechanics dates back to 1882 with the publication of the paper "On the contact of elastic solids" ("Ueber die Berührung fester elastischer Körper") by Heinrich Hertz. Hertz was attempting to understand how the optical properties of multiple, stacked lenses
might change with the force
holding them together. Hertzian contact stress refers to the localized stresses that develop as two curved surfaces come in contact and deform slightly under the imposed loads. This amount of deformation is dependent on the modulus of elasticity of the material in contact. It gives the contact stress as a function of the normal contact force, the radii of curvature of both bodies and the modulus of elasticity of both bodies. Hertzian contact stress forms the foundation for the equations for load bearing capabilities and fatigue
life in bearings, gears, and any other bodies where two surfaces are in contact.
 Classical contact mechanics is most notably associated with Heinrich Hertz. In 1882 Hertz solved the problem involving contact between two elastic bodies with curved surfaces. This still-relevant classical solution provides a foundation for modern problems in contact mechanics. For example, in mechanical engineering
Classical contact mechanics is most notably associated with Heinrich Hertz. In 1882 Hertz solved the problem involving contact between two elastic bodies with curved surfaces. This still-relevant classical solution provides a foundation for modern problems in contact mechanics. For example, in mechanical engineering
and tribology, Hertzian contact stress, is a description of the stress within mating parts. In general, the Hertzian contact stress usually refers to the stress close to the area of contact between two spheres of different radii.
It was not until nearly one hundred years later that Johnson
, Kendall, and Roberts found a similar solution for the case of adhesive
contact. This theory was rejected by Boris Derjaguin
and co-workers who proposed a different theory of adhesion in the 1970s. The Derjaguin model came to be known as the DMT (after Derjaguin, Muller and Toporov) model, and the Johnson et al. model came to be known as the JKR (after Johnson, Kendall and Roberts) model for adhesive elastic contact. This rejection proved to be instrumental in the development of the Tabor and later Maugis parameters that quantify which contact model (of the JKR and DMT models) represent adhesive contact better for specific materials.
Further advancement in the field of contact mechanics in the mid-twentieth century may be attributed to names such as Bowden and Tabor
. Bowden and Tabor were the first to emphasize the importance of surface roughness for bodies in contact. Through investigation of the surface roughness, the true contact area between friction partners is found to be less than the apparent contact area. Such understanding also drastically changed the direction of undertakings in tribology. The works of Bowden and Tabor yielded several theories in contact mechanics of rough surfaces.
The contributions of Archard (1957) must also be mentioned in discussion of pioneering works in this field. Archard concluded that, even for rough elastic surfaces, the contact area is approximately proportional to the normal force
. Further important insights along these lines were provided by Greenwood and Williamson (1966), Bush (1975), and Persson (2002). The main findings of these works were that the true contact surface in rough materials is generally proportional to the normal force, while the parameters of individual micro-contacts (i.e. pressure, size of the micro-contact) are only weakly dependent upon the load.
of radius
 indents an elastic half-space
indents an elastic half-space
to depth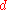 , and thus creates a contact area of radius
, and thus creates a contact area of radius  . The applied force
. The applied force  is related to the displacement
is related to the displacement 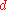 by
by
where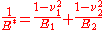
and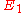 ,
,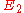 are the elastic moduli
are the elastic moduli
and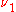 ,
, the Poisson's ratio
the Poisson's ratio
s associated with each body.
 and
and 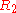 , the area of contact is a circle of radius
, the area of contact is a circle of radius  . The distribution of normal traction in the contact area as a function of distance from the center of the circle is
. The distribution of normal traction in the contact area as a function of distance from the center of the circle is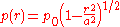
where is the maximum contact pressure given by
is the maximum contact pressure given by
where the effective radius is defined as
is defined as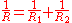
The area of contact is related to the applied load by the equation
by the equation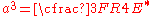
The depth of indentation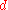 is related to the maximum contact pressure by
is related to the maximum contact pressure by
The maximum shear stress occurs in the interior at for
for 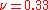 .
.
Contact between two crossed cylinders of equal radius
This is equivalent to contact between a sphere of radius  and a plane (see above).
and a plane (see above).
is pressed into an elastic half-space, it creates a pressure distribution described by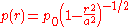
where is the radius of the cylinder and
is the radius of the cylinder and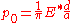
The relationship between the indentation depth and the normal force is given by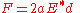
of an elastic half-space using a rigid conical
indenter, the indentation depth and contact radius are related by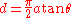
with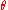 defined as the angle between the plane and the side surface of the cone. The pressure distribution takes on the form
defined as the angle between the plane and the side surface of the cone. The pressure distribution takes on the form
The stress has a logarithm
ic singularity
on the tip of the cone. The total force is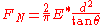

The radii of curvature are entirely absent from this relationship. The contact radius is described through the usual relationship
with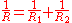
as in contact between two spheres. The maximum pressure is equal to
are transmitted between the bodies where they touch, so problems in contact mechanics can become quite sophisticated. In addition, the contact stresses are usually a nonlinear function of the deformation. To simplify the solution procedure, a frame of reference
is usually defined in which the objects (possibly in motion relative to one another) are static. They interact through surface tractions (or pressures/stresses) at their interface.
As an example, consider two objects which meet at some surface in the (
in the ( ,
,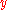 )-plane with the
)-plane with the  -axis assumed normal to the surface. One of the bodies will experience a normally-directed pressure
-axis assumed normal to the surface. One of the bodies will experience a normally-directed pressure
distribution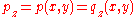 and in-plane surface traction distributions
and in-plane surface traction distributions 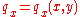 and
and 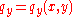 over the region
over the region  . In terms of a Newtonian force balance, the forces:
. In terms of a Newtonian force balance, the forces: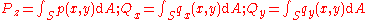
must be equal and opposite to the forces established in the other body. The moments corresponding to these forces: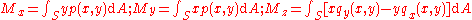
are also required to cancel between bodies so that they are kinematically
immobile.
Additional complications arise when some or all these assumptions are violated and such contact problems are usually called non-Hertzian.
 Analytical solution methods for non-adhesive contact problem can be classified into two types based on the geometry of the area of contact. A conforming contact is one in which the two bodies touch at multiple points before any deformation takes place (i.e., they just "fit together"). A non-conforming contact is one in which the shapes of the bodies are dissimilar enough that, under zero load, they only touch at a point (or possibly along a line). In the non-conforming case, the contact area is small compared to the sizes of the objects and the stresses
Analytical solution methods for non-adhesive contact problem can be classified into two types based on the geometry of the area of contact. A conforming contact is one in which the two bodies touch at multiple points before any deformation takes place (i.e., they just "fit together"). A non-conforming contact is one in which the shapes of the bodies are dissimilar enough that, under zero load, they only touch at a point (or possibly along a line). In the non-conforming case, the contact area is small compared to the sizes of the objects and the stresses
are highly concentrated in this area. Such a contact is called concentrated, otherwise it is called diversified.
A common approach in linear elasticity
is to superpose
a number of solutions each of which corresponds to a point load acting over the area of contact. For example, in the case of loading of a half-plane, the Flamant solution
is often used as a starting point and then generalized to various shapes of the area of contact. The force and moment balances between the two bodies in contact act as additional constraints to the solution.
of linear elasticity subject to the traction boundary conditions: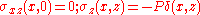
where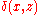 is the Dirac delta function
is the Dirac delta function
. The boundary conditions state that are no shear stresses on the surface and a singular normal force P is applied at (0,0). Applying these conditions to the governing equations of elasticity produces the result
for some point, , in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, the strain
, in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, the strain
components and thus the displacements
of all material points may be determined.
Normal loading over a region
Suppose, rather than a point load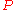 , a distributed load
, a distributed load 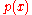 is applied to the surface instead, over the range
is applied to the surface instead, over the range  . The principle of linear superposition can be applied to determine the resulting stress field as the solution to the integral
. The principle of linear superposition can be applied to determine the resulting stress field as the solution to the integral
equations: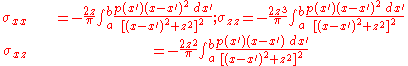
Shear loading over a region
The same principle applies for loading on the surface in the plane of the surface. These kinds of tractions would tend to arise as a result of friction. The solution is similar the above (for both singular loads and distributed loads
and distributed loads 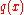 ) but altered slightly:
) but altered slightly:
These results may themselves be superposed onto those given above for normal loading to deal with more complex loads.
. Besides the standard equations describing the deformation and motion of bodies two additional inequalities can be formulated. The first simply restricts the motion and deformation of the bodies by the assumption that no penetration can occur. Hence the gap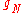 between two bodies can only be positive or zero
between two bodies can only be positive or zero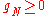
where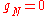 denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the contact pressure
denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the contact pressure 

Since for contact,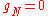 , the contact pressure is always negative,
, the contact pressure is always negative,  , and further for non contact the gap is open,
, and further for non contact the gap is open,  , and the contact pressure is zero,
, and the contact pressure is zero,  , the so called Kuhn–Tucker form of the contact constraints can be written as
, the so called Kuhn–Tucker form of the contact constraints can be written as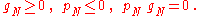
These conditions are valid in a general way. The mathematical formulation of the gap depends upon the kinematics of the underlying theory of the solid (e.g., linear or nonlinear solid in two- or three dimensions, beam or shell
model).
 is much smaller than the apparent contact area
is much smaller than the apparent contact area  . In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force
. In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force  by
by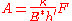
with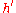 equal to the root mean square (also known as the quadratic mean) of the surface slope and
equal to the root mean square (also known as the quadratic mean) of the surface slope and  . The median pressure in the true contact surface
. The median pressure in the true contact surface
can be reasonably estimated as half of the effective elastic modulus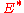 multiplied with the root mean square of the surface slope
multiplied with the root mean square of the surface slope 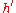 .
.
For the situation where the asperities on the two surfaces have a Gaussian height distribution and the peaks can be assumed to be spherical, the average contact pressure is sufficient to cause yield when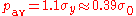 where
where 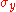 is the uniaxial yield stress and
is the uniaxial yield stress and 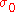 is the indentation hardness. Greenwood and Williamson defined a dimensionless parameter
is the indentation hardness. Greenwood and Williamson defined a dimensionless parameter  called the plasticity index that could be used to determine whether contact would be elastic or plastic.
called the plasticity index that could be used to determine whether contact would be elastic or plastic.
The Greenwood-Williamson model requires knowledge of two statistically dependent quantities; the standard deviation of the surface roughness and the curvature of the asperity peaks. An alternative definition of the plasticity index has been given by Mikic. Yield occurs when the pressure is greater than the uniaxial yield stress. Since the yield stress is proportional to the indentation hardness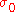 , Micic defined the plasticity index for elastic-plastic contact to be
, Micic defined the plasticity index for elastic-plastic contact to be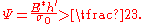
In this definition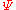 represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For
represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For 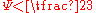 , the surface behaves elastically during contact.
, the surface behaves elastically during contact.
In both the Greenwood-Williamson and Mikic models the load is assumed to be proportional to the deformed area. Hence, whether the system behaves plastically or elastically is independent of the applied normal force.
s. Bradley's van der Waals model provides a means of calculating the tensile force between two rigid spheres with perfectly smooth surfaces. The Hertzian model of contact does not consider adhesion possible. However, in the late 1960s, several contradictions were observed when the Hertz theory was compared with experiments involving contact between rubber and glass spheres.
It was observed that, though Hertz theory applied at large loads, at low loads
This indicated that adhesive forces were at work. The Johnson-Kendall-Roberts (JKR) model and the Derjaguin-Muller-Toporov (DMT) models were the first to incorporate adhesion into Hertzian contact.
 from each other can be derived from the Lennard-Jones potential
from each other can be derived from the Lennard-Jones potential
. With that assumption we can write
where is the force (positive in compression),
is the force (positive in compression), 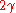 is the is the total surface energy of both surfaces per unit area, and
is the is the total surface energy of both surfaces per unit area, and  is the equilibrium separation of the two atomic planes.
is the equilibrium separation of the two atomic planes.
The Bradley model applied the Lennard-Jones potential to find the force of adhesion between two rigid spheres. The total force between the spheres is found to be
where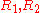 are the radii of the two spheres.
are the radii of the two spheres.
The two spheres separate completely when the pull-off force is achieved at at which point
at which point
and the loss in surface energy
. The JKR model considers the effect of contact pressure and adhesion only inside the area of contact. The general solution for the pressure distribution in the contact area in the JKR model is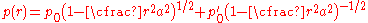
Note that in the original Hertz theory, the term containing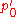 was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres
was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres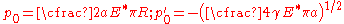
where is the radius of the area of contact,
is the radius of the area of contact,  is the applied force,
is the applied force, 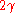 is the total surface energy of both surfaces per unit contact area,
is the total surface energy of both surfaces per unit contact area,
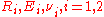 are the radii, Young's moduli, and Poisson's ratios of the two spheres, and
are the radii, Young's moduli, and Poisson's ratios of the two spheres, and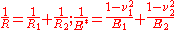
The approach distance between the two spheres is given by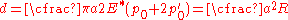
The Hertz equation for the area of contact between two spheres, modified to take into account the surface energy, has the form
When the surface energy is zero, , the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is
, the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is
The tensile load at which the spheres are separated, i.e., , is predicted to be
, is predicted to be
This force is also called the pull-off force.
Note that this force is independent of the moduli of the two spheres. However, there is another possible solution for the value of at this load. This is the critical contact area
at this load. This is the critical contact area 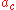 , given by
, given by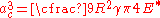
If we define the work of adhesion as
where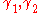 are the adhesive energies of the two surfaces and
are the adhesive energies of the two surfaces and 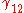 is an interaction term, we can write the JKR contact radius as
is an interaction term, we can write the JKR contact radius as
The tensile load at separation is
and the critical contact radius is given by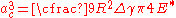
The critical depth of penetration is
The area of contact between two spheres from DMT theory is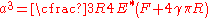
and the pull-off force is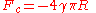
When the pull-off force is achieved the contact area becomes zero and there is no singularity in the contact stresses at the edge of the contact area.
In terms of the work of adhesion
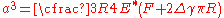
and
 ) defined as
) defined as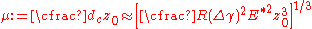
where is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which
is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which  is large. The DMT theory applies for small, stiff spheres with small values of
is large. The DMT theory applies for small, stiff spheres with small values of  .
.

where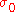 is the maximum force predicted by the Lennard-Jones potential and
is the maximum force predicted by the Lennard-Jones potential and  is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for
is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for 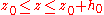 . There is not further penetration in compression. Perfect contact occurs in an area of radius
. There is not further penetration in compression. Perfect contact occurs in an area of radius  and adhesive forces of magnitude
and adhesive forces of magnitude 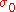 extend to an area of radius
extend to an area of radius  . In the region
. In the region 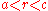 , the two surfaces are separated by a distance
, the two surfaces are separated by a distance 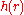 with
with 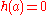 and
and 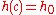 . The ratio
. The ratio  is defined as
is defined as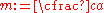 .
.
In the Maugis-Dugdale theory, the surface traction distribution is divided into two parts - one due to the Hertz contact pressure and the other from the Dugdale adhesive stress. Hertz contact is assumed in the region . The contribution to the surface traction from the Hertz pressure is given by
. The contribution to the surface traction from the Hertz pressure is given by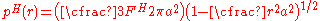
where the Hertz contact force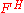 is given by
is given by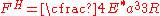
The penetration due to elastic compression is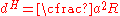
The vertical displacement at is
is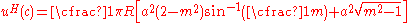
and the separation between the two surfaces at is
is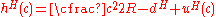
The surface traction distribution due to the adhesive Dugdale stress is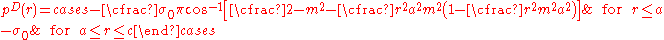
The total adhesive force is then given by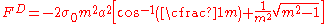
The compression due to Dugdale adhesion is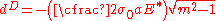
and the gap at is
is
The net traction on the contact area is then given by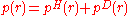 and the net contact force is
and the net contact force is 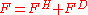 . When
. When  the adhesive traction drops to zero.
the adhesive traction drops to zero.
Non-dimensionalized values of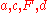 are introduced at this stage that are defied as
are introduced at this stage that are defied as
In addition, Maugis proposed a parameter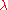 which is equivalent to the Tabor coefficient. This parameter is defined as
which is equivalent to the Tabor coefficient. This parameter is defined as
Then the net contact force may be expressed as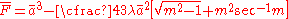
and the elastic compression as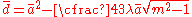
The equation for the cohesive gap between the two bodies takes the form
This equation can be solved to obtain values of for various values of
for various values of  and
and  . For large values of
. For large values of  ,
,  and the JKR model is obtained. For small values of
and the JKR model is obtained. For small values of 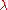 the DMT model is retrieved.
the DMT model is retrieved.
 is not known a-priori. The Carpick-Ogletree-Salmeron approximate solution simplifies the process by using the following relation to determine the contact radius
is not known a-priori. The Carpick-Ogletree-Salmeron approximate solution simplifies the process by using the following relation to determine the contact radius  :
: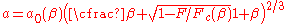
where is the contact area at zero load, and
is the contact area at zero load, and 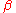 is a transition parameter that is related to
is a transition parameter that is related to 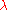 by
by
The case corresponds exactly to JKR theory while
corresponds exactly to JKR theory while  corresponds to DMT theory.
corresponds to DMT theory.
For intermediate cases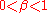 the COS model corresponds closely to the Maugis-Dugdale solution for
the COS model corresponds closely to the Maugis-Dugdale solution for  .
.
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
of solids that touch each other at one or more points. The physical and mathematical formulation of the subject is built upon the mechanics of materials and continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
and focuses on computations involving elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
, viscoelastic
Viscoelasticity
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just...
, and plastic bodies in static
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
or dynamic contact. Central aspects in contact mechanics are the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
s and adhesion
Adhesion
Adhesion is any attraction process between dissimilar molecular species that can potentially bring them in close contact. By contrast, cohesion takes place between similar molecules....
acting perpendicular to the contacting bodies' surfaces, the normal direction, and the friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
al stresses acting tangentially
Tangential and normal components
In mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector...
between the surfaces. This page focuses mainly on the normal direction, i.e. on frictionless contact mechanics. Frictional contact mechanics
Frictional contact mechanics
Contact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction...
is discussed separately.
Contact mechanics is foundational to the field of mechanical engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
; it provides necessary information for the safe and energy efficient design of technical systems and for the study of tribology
Tribology
Tribology is the science and engineering of interacting surfaces in relative motion. It includes the study and application of the principles of friction, lubrication and wear...
and indentation hardness
Indentation hardness
Indentation hardness tests are used to determine the hardness of a material to deformation. Several such tests exist, wherein the examined material is indented until an impression is formed; these tests can be performed on a macroscopic or microscopic scale....
. Principles of contacts mechanics can be applied in areas such as locomotive wheel-rail contact, coupling
Coupling
A coupling is a device used to connect two shafts together at their ends for the purpose of transmitting power. Couplings do not normally allow disconnection of shafts during operation, however there are torque limiting couplings which can slip or disconnect when some torque limit is exceeded.The...
devices, braking
Brake
A brake is a mechanical device which inhibits motion. Its opposite component is a clutch. The rest of this article is dedicated to various types of vehicular brakes....
systems, tire
Tire
A tire or tyre is a ring-shaped covering that fits around a wheel rim to protect it and enable better vehicle performance by providing a flexible cushion that absorbs shock while keeping the wheel in close contact with the ground...
s, bearings
Bearing (mechanical)
A bearing is a device to allow constrained relative motion between two or more parts, typically rotation or linear movement. Bearings may be classified broadly according to the motions they allow and according to their principle of operation as well as by the directions of applied loads they can...
, combustion engines
Internal combustion engine
The internal combustion engine is an engine in which the combustion of a fuel occurs with an oxidizer in a combustion chamber. In an internal combustion engine, the expansion of the high-temperature and high -pressure gases produced by combustion apply direct force to some component of the engine...
, mechanical linkage
Linkage (mechanical)
A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
s, gasket
Gasket
thumb|sright|250px|Some seals and gaskets1. [[o-ring]]2. fiber [[Washer |washer]]3. paper gaskets4. [[cylinder head]] [[head gasket|gasket]]...
seals, metalworking
Metalworking
Metalworking is the process of working with metals to create individual parts, assemblies, or large scale structures. The term covers a wide range of work from large ships and bridges to precise engine parts and delicate jewelry. It therefore includes a correspondingly wide range of skills,...
, metal forming, ultrasonic welding
Ultrasonic welding
Ultrasonic welding is an industrial technique whereby high-frequency ultrasonic acoustic vibrations are locally applied to workpieces being held together under pressure to create a solid-state weld. It is commonly used for plastics, and especially for joining dissimilar materials...
, electrical contacts
Electrical connector
An electrical connector is an electro-mechanical device for joining electrical circuits as an interface using a mechanical assembly. The connection may be temporary, as for portable equipment, require a tool for assembly and removal, or serve as a permanent electrical joint between two wires or...
, and many others. Current challenges faced in the field may include stress analysis
Stress analysis
Stress analysis is an engineering discipline that determines the stress in materials and structures subjected to static or dynamic forces or loads. A stress analysis is required for the study and design of structures, e.g., tunnels, dams, mechanical parts, and structural frames among others, under...
of contact and coupling members and the influence of lubrication
Lubrication
Lubrication is the process, or technique employed to reduce wear of one or both surfaces in close proximity, and moving relative to each another, by interposing a substance called lubricant between the surfaces to carry or to help carry the load between the opposing surfaces. The interposed...
and material design
Design
Design as a noun informally refers to a plan or convention for the construction of an object or a system while “to design” refers to making this plan...
on friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
and wear
Wear
In materials science, wear is erosion or sideways displacement of material from its "derivative" and original position on a solid surface performed by the action of another surface....
. Applications of contact mechanics further extend into the micro
Microtechnology
Microtechnology is technology with features near one micrometre .In the 1960s, scientists learned that by arraying large numbers of microscopic transistors on a single chip, microelectronic circuits could be built that dramatically improved performance, functionality, and reliability, all while...
- and nanotechnological
Nanotechnology
Nanotechnology is the study of manipulating matter on an atomic and molecular scale. Generally, nanotechnology deals with developing materials, devices, or other structures possessing at least one dimension sized from 1 to 100 nanometres...
realm.
The original work in contact mechanics dates back to 1882 with the publication of the paper "On the contact of elastic solids" ("Ueber die Berührung fester elastischer Körper") by Heinrich Hertz. Hertz was attempting to understand how the optical properties of multiple, stacked lenses
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
might change with the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
holding them together. Hertzian contact stress refers to the localized stresses that develop as two curved surfaces come in contact and deform slightly under the imposed loads. This amount of deformation is dependent on the modulus of elasticity of the material in contact. It gives the contact stress as a function of the normal contact force, the radii of curvature of both bodies and the modulus of elasticity of both bodies. Hertzian contact stress forms the foundation for the equations for load bearing capabilities and fatigue
Fatigue (material)
'In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.Fatigue occurs...
life in bearings, gears, and any other bodies where two surfaces are in contact.
History

Mechanical engineering
Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
and tribology, Hertzian contact stress, is a description of the stress within mating parts. In general, the Hertzian contact stress usually refers to the stress close to the area of contact between two spheres of different radii.
It was not until nearly one hundred years later that Johnson
Kenneth L. Johnson
Kenneth Langstreth Johnson is a British engineer.He was elected a Fellow of the Royal Society in 1982 and won their Royal Medal in 2003 "In recognition of his outstanding work in the field of contact mechanics"He was also awarded the 2006 Timoshenko Medal....
, Kendall, and Roberts found a similar solution for the case of adhesive
Adhesion
Adhesion is any attraction process between dissimilar molecular species that can potentially bring them in close contact. By contrast, cohesion takes place between similar molecules....
contact. This theory was rejected by Boris Derjaguin
Boris Derjaguin
Professor Boris Vladimirovich Derjaguin was one of the renowned Soviet/Russian chemists of the twentieth century. As a member of the Russian Academy of Sciences he laid the foundation of the modern science of colloids and surfaces...
and co-workers who proposed a different theory of adhesion in the 1970s. The Derjaguin model came to be known as the DMT (after Derjaguin, Muller and Toporov) model, and the Johnson et al. model came to be known as the JKR (after Johnson, Kendall and Roberts) model for adhesive elastic contact. This rejection proved to be instrumental in the development of the Tabor and later Maugis parameters that quantify which contact model (of the JKR and DMT models) represent adhesive contact better for specific materials.
Further advancement in the field of contact mechanics in the mid-twentieth century may be attributed to names such as Bowden and Tabor
David Tabor
David Tabor was a British physicist who coined the word tribology for the study of frictional interaction between surfaces.He was Professor of Physics in the University of Cambridge, then Emeritus professor...
. Bowden and Tabor were the first to emphasize the importance of surface roughness for bodies in contact. Through investigation of the surface roughness, the true contact area between friction partners is found to be less than the apparent contact area. Such understanding also drastically changed the direction of undertakings in tribology. The works of Bowden and Tabor yielded several theories in contact mechanics of rough surfaces.
The contributions of Archard (1957) must also be mentioned in discussion of pioneering works in this field. Archard concluded that, even for rough elastic surfaces, the contact area is approximately proportional to the normal force
Normal force
In mechanics, the normal force F_n\ is the component, perpendicular to the surface of contact, of the contact force exerted on an object by, for example, the surface of a floor or wall, preventing the object from penetrating the surface.The normal force is one of the components of the ground...
. Further important insights along these lines were provided by Greenwood and Williamson (1966), Bush (1975), and Persson (2002). The main findings of these works were that the true contact surface in rough materials is generally proportional to the normal force, while the parameters of individual micro-contacts (i.e. pressure, size of the micro-contact) are only weakly dependent upon the load.
Classical solutions for non-adhesive elastic contact
The theory of contact between elastic bodies can be used to find contact areas and indentation depths for simple geometries. Some commonly used solutions are listed below. The theory used to compute these solutions is discussed later in the article.Contact between a sphere and an elastic half-space
An elastic sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
 indents an elastic half-space
indents an elastic half-spaceHalf-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
to depth
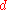 , and thus creates a contact area of radius
, and thus creates a contact area of radius  . The applied force
. The applied force  is related to the displacement
is related to the displacement 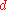 by
by
where
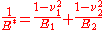
and
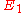 ,
,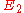 are the elastic moduli
are the elastic moduliElastic modulus
An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
and
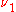 ,
, the Poisson's ratio
the Poisson's ratioPoisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
s associated with each body.
Contact between two spheres
For contact between two spheres of radii and
and 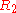 , the area of contact is a circle of radius
, the area of contact is a circle of radius  . The distribution of normal traction in the contact area as a function of distance from the center of the circle is
. The distribution of normal traction in the contact area as a function of distance from the center of the circle is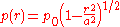
where
 is the maximum contact pressure given by
is the maximum contact pressure given by
where the effective radius
 is defined as
is defined as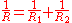
The area of contact is related to the applied load
 by the equation
by the equation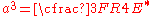
The depth of indentation
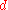 is related to the maximum contact pressure by
is related to the maximum contact pressure by
The maximum shear stress occurs in the interior at
 for
for 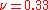 .
.Contact between two crossed cylinders of equal radius 
This is equivalent to contact between a sphere of radius  and a plane (see above).
and a plane (see above).Contact between a rigid cylinder and an elastic half-space
If a rigid cylinderCylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
is pressed into an elastic half-space, it creates a pressure distribution described by
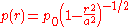
where
 is the radius of the cylinder and
is the radius of the cylinder and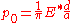
The relationship between the indentation depth and the normal force is given by
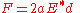
Contact between a rigid conical indenter and an elastic half-space
In the case of indentationIndentation
An indentation may refer to:* A notch, or deep recesses; for instance in a coastline, or a carving in rock* The placement of text farther to the right to separate it from surrounding text....
of an elastic half-space using a rigid conical
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
indenter, the indentation depth and contact radius are related by
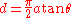
with
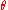 defined as the angle between the plane and the side surface of the cone. The pressure distribution takes on the form
defined as the angle between the plane and the side surface of the cone. The pressure distribution takes on the form
The stress has a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
on the tip of the cone. The total force is
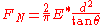
Contact between two cylinders with parallel axes
In contact between two cylinders with parallel axes, the force is linearly proportional to the indentation depth:
The radii of curvature are entirely absent from this relationship. The contact radius is described through the usual relationship

with
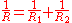
as in contact between two spheres. The maximum pressure is equal to

Hertzian theory of non-adhesive elastic contact
The classical theory of contact focused primarily on non-adhesive contact where no tension force is allowed to occur within the contact area, i.e., contacting bodies can be separated without adhesion forces. Several analytical and numerical approaches have been used to solve contact problems that satisfy the no-adhesion condition. Complex forces and momentsMoment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
are transmitted between the bodies where they touch, so problems in contact mechanics can become quite sophisticated. In addition, the contact stresses are usually a nonlinear function of the deformation. To simplify the solution procedure, a frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
is usually defined in which the objects (possibly in motion relative to one another) are static. They interact through surface tractions (or pressures/stresses) at their interface.
As an example, consider two objects which meet at some surface
 in the (
in the ( ,
,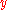 )-plane with the
)-plane with the  -axis assumed normal to the surface. One of the bodies will experience a normally-directed pressure
-axis assumed normal to the surface. One of the bodies will experience a normally-directed pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
distribution
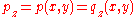 and in-plane surface traction distributions
and in-plane surface traction distributions 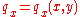 and
and 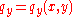 over the region
over the region  . In terms of a Newtonian force balance, the forces:
. In terms of a Newtonian force balance, the forces: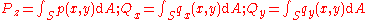
must be equal and opposite to the forces established in the other body. The moments corresponding to these forces:
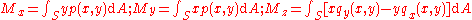
are also required to cancel between bodies so that they are kinematically
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
immobile.
Assumptions in Hertzian theory
The following assumptions are made in determining the solutions of Hertzian contact problems:- the strains are small and within the elastic limit,
- each body can be considered an elastic half-space, i.e., the area of contact is much smaller than the characteristic radius of the body,
- the surfaces are continuous and non-conforming, and
- the surfaces are frictionless.
Additional complications arise when some or all these assumptions are violated and such contact problems are usually called non-Hertzian.
Analytical solution techniques

Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
are highly concentrated in this area. Such a contact is called concentrated, otherwise it is called diversified.
A common approach in linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
is to superpose
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
a number of solutions each of which corresponds to a point load acting over the area of contact. For example, in the case of loading of a half-plane, the Flamant solution
Flamant solution
The Flamant solution provides expressions for the stresses and displacements in a linear elastic wedge loaded by point forces at its sharp end. This solution was developed by A...
is often used as a starting point and then generalized to various shapes of the area of contact. The force and moment balances between the two bodies in contact act as additional constraints to the solution.
Point contact on a (2D) half-plane
A starting point for solving contact problems is to understand the effect of a "point-load" applied to an isotropic, homogeneous, and linear elastic half-plane, shown in the figure to the right. The problem may be either be plane stress or plane strain. This is a boundary value problemBoundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
of linear elasticity subject to the traction boundary conditions:
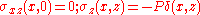
where
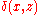 is the Dirac delta function
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. The boundary conditions state that are no shear stresses on the surface and a singular normal force P is applied at (0,0). Applying these conditions to the governing equations of elasticity produces the result

for some point,
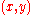 , in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, the strain
, in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, the strainStrain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
components and thus the displacements
Displacement field (mechanics)
A displacement field is an assignment of displacement vectors for all points in a region or body that is displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position...
of all material points may be determined.
Normal loading over a region 
Suppose, rather than a point load
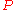 , a distributed load
, a distributed load 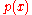 is applied to the surface instead, over the range
is applied to the surface instead, over the range  . The principle of linear superposition can be applied to determine the resulting stress field as the solution to the integral
. The principle of linear superposition can be applied to determine the resulting stress field as the solution to the integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
equations:
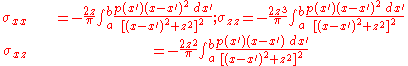
Shear loading over a region 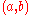
The same principle applies for loading on the surface in the plane of the surface. These kinds of tractions would tend to arise as a result of friction. The solution is similar the above (for both singular loads
 and distributed loads
and distributed loads  ) but altered slightly:
) but altered slightly:
These results may themselves be superposed onto those given above for normal loading to deal with more complex loads.
Point contact on a (3D) half-space
Analogously to the Flamant solution for the 2D half-plane, fundamental solutions are known for the linearly elastic 3D half-space as well. These were found by Boussinesq for a concentrated normal load and by Cerutti for a tangential load. See the section on this in Linear elasticity.Numerical solution techniques
Distinctions between conforming and non-conforming contact do not have to be made when numerical solution schemes are employed to solve contact problems. These methods do not rely on further assumptions within the solution process since they base solely on the general formulation of the underlying equations. Besides the standard equations describing the deformation and motion of bodies two additional inequalities can be formulated. The first simply restricts the motion and deformation of the bodies by the assumption that no penetration can occur. Hence the gap
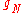 between two bodies can only be positive or zero
between two bodies can only be positive or zero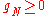
where
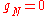 denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the contact pressure
denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the contact pressure 

Since for contact,
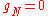 , the contact pressure is always negative,
, the contact pressure is always negative,  , and further for non contact the gap is open,
, and further for non contact the gap is open,  , and the contact pressure is zero,
, and the contact pressure is zero,  , the so called Kuhn–Tucker form of the contact constraints can be written as
, the so called Kuhn–Tucker form of the contact constraints can be written as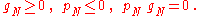
These conditions are valid in a general way. The mathematical formulation of the gap depends upon the kinematics of the underlying theory of the solid (e.g., linear or nonlinear solid in two- or three dimensions, beam or shell
Plate theory
In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...
model).
Non-adhesive contact between rough surfaces
When two bodies with rough surfaces are pressed into each other, the true contact area is much smaller than the apparent contact area
is much smaller than the apparent contact area  . In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force
. In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force  by
by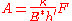
with
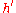 equal to the root mean square (also known as the quadratic mean) of the surface slope and
equal to the root mean square (also known as the quadratic mean) of the surface slope and  . The median pressure in the true contact surface
. The median pressure in the true contact surface
can be reasonably estimated as half of the effective elastic modulus
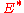 multiplied with the root mean square of the surface slope
multiplied with the root mean square of the surface slope 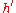 .
.For the situation where the asperities on the two surfaces have a Gaussian height distribution and the peaks can be assumed to be spherical, the average contact pressure is sufficient to cause yield when
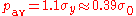 where
where 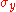 is the uniaxial yield stress and
is the uniaxial yield stress and 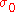 is the indentation hardness. Greenwood and Williamson defined a dimensionless parameter
is the indentation hardness. Greenwood and Williamson defined a dimensionless parameter  called the plasticity index that could be used to determine whether contact would be elastic or plastic.
called the plasticity index that could be used to determine whether contact would be elastic or plastic.The Greenwood-Williamson model requires knowledge of two statistically dependent quantities; the standard deviation of the surface roughness and the curvature of the asperity peaks. An alternative definition of the plasticity index has been given by Mikic. Yield occurs when the pressure is greater than the uniaxial yield stress. Since the yield stress is proportional to the indentation hardness
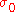 , Micic defined the plasticity index for elastic-plastic contact to be
, Micic defined the plasticity index for elastic-plastic contact to be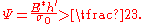
In this definition
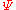 represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For
represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For 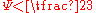 , the surface behaves elastically during contact.
, the surface behaves elastically during contact.In both the Greenwood-Williamson and Mikic models the load is assumed to be proportional to the deformed area. Hence, whether the system behaves plastically or elastically is independent of the applied normal force.
Adhesive contact between elastic bodies
When two solid surfaces are brought into close proximity to each other they experience attractive van der Waals forceVan der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
s. Bradley's van der Waals model provides a means of calculating the tensile force between two rigid spheres with perfectly smooth surfaces. The Hertzian model of contact does not consider adhesion possible. However, in the late 1960s, several contradictions were observed when the Hertz theory was compared with experiments involving contact between rubber and glass spheres.
It was observed that, though Hertz theory applied at large loads, at low loads
- the area of contact was larger than that predicted by Hertz theory,
- the area of contact had a non-zero value even when the load was removed, and
- there was strong adhesion if the contacting surfaces were clean and dry.
This indicated that adhesive forces were at work. The Johnson-Kendall-Roberts (JKR) model and the Derjaguin-Muller-Toporov (DMT) models were the first to incorporate adhesion into Hertzian contact.
Bradley model of rigid contact
It is commonly assumed that the surface force between two atomic planes at a distance from each other can be derived from the Lennard-Jones potential
from each other can be derived from the Lennard-Jones potentialLennard-Jones potential
The Lennard-Jones potential is a mathematically simple model that approximates the interaction between a pair of neutral atoms or molecules. A form of the potential was first proposed in 1924 by John Lennard-Jones...
. With that assumption we can write

where
 is the force (positive in compression),
is the force (positive in compression), 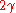 is the is the total surface energy of both surfaces per unit area, and
is the is the total surface energy of both surfaces per unit area, and  is the equilibrium separation of the two atomic planes.
is the equilibrium separation of the two atomic planes.The Bradley model applied the Lennard-Jones potential to find the force of adhesion between two rigid spheres. The total force between the spheres is found to be

where
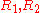 are the radii of the two spheres.
are the radii of the two spheres.The two spheres separate completely when the pull-off force is achieved at
 at which point
at which point
Johnson-Kendall-Roberts (JKR) model of elastic contact
To incorporate the effect of adhesion in Hertzian contact, Johnson, Kendall, and Roberts formulated the JKR theory of adhesive contact using a balance between the stored elastic energyElastic energy
Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system as work is performed to distort its volume or shape....
and the loss in surface energy
Surface energy
Surface energy quantifies the disruption of intermolecular bonds that occur when a surface is created. In the physics of solids, surfaces must be intrinsically less energetically favorable than the bulk of a material, otherwise there would be a driving force for surfaces to be created, removing...
. The JKR model considers the effect of contact pressure and adhesion only inside the area of contact. The general solution for the pressure distribution in the contact area in the JKR model is
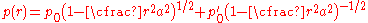
Note that in the original Hertz theory, the term containing
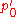 was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres
was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres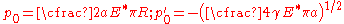
where
 is the radius of the area of contact,
is the radius of the area of contact,  is the applied force,
is the applied force, 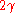 is the total surface energy of both surfaces per unit contact area,
is the total surface energy of both surfaces per unit contact area,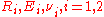 are the radii, Young's moduli, and Poisson's ratios of the two spheres, and
are the radii, Young's moduli, and Poisson's ratios of the two spheres, and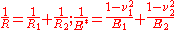
The approach distance between the two spheres is given by
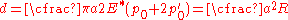
The Hertz equation for the area of contact between two spheres, modified to take into account the surface energy, has the form

When the surface energy is zero,
 , the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is
, the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is
The tensile load at which the spheres are separated, i.e.,
 , is predicted to be
, is predicted to be
This force is also called the pull-off force.
Note that this force is independent of the moduli of the two spheres. However, there is another possible solution for the value of
 at this load. This is the critical contact area
at this load. This is the critical contact area 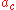 , given by
, given by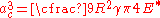
If we define the work of adhesion as

where
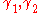 are the adhesive energies of the two surfaces and
are the adhesive energies of the two surfaces and 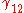 is an interaction term, we can write the JKR contact radius as
is an interaction term, we can write the JKR contact radius as
The tensile load at separation is

and the critical contact radius is given by
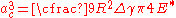
The critical depth of penetration is

Derjaguin-Muller-Toporov (DMT) model of elastic contact
The Derjaguin-Muller-Toporov (DMT) model is an alternative model for adhesive contact which assumes that the contact profile remains the same as in Hertzian contact but with additional attractive interactions outside the area of contact.The area of contact between two spheres from DMT theory is
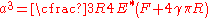
and the pull-off force is
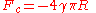
When the pull-off force is achieved the contact area becomes zero and there is no singularity in the contact stresses at the edge of the contact area.
In terms of the work of adhesion

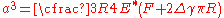
and

Tabor coefficient
In 1977, Tabor showed that the apparent contradiction between the JKR and DMT theories could be resolved by noting that the two theories were the extreme limits of a single theory parametrized by the Tabor coefficient ( ) defined as
) defined as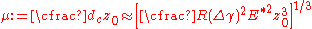
where
 is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which
is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which  is large. The DMT theory applies for small, stiff spheres with small values of
is large. The DMT theory applies for small, stiff spheres with small values of  .
.Maugis-Dugdale model of elastic contact
Further improvement to the Tabor idea was provided by Maugis who represented the surface force in terms of a Dugdale cohesive zone approximation such that the work of adhesion is given by
where
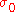 is the maximum force predicted by the Lennard-Jones potential and
is the maximum force predicted by the Lennard-Jones potential and  is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for
is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for 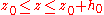 . There is not further penetration in compression. Perfect contact occurs in an area of radius
. There is not further penetration in compression. Perfect contact occurs in an area of radius  and adhesive forces of magnitude
and adhesive forces of magnitude 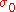 extend to an area of radius
extend to an area of radius  . In the region
. In the region 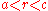 , the two surfaces are separated by a distance
, the two surfaces are separated by a distance 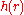 with
with 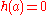 and
and 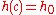 . The ratio
. The ratio  is defined as
is defined as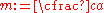 .
.In the Maugis-Dugdale theory, the surface traction distribution is divided into two parts - one due to the Hertz contact pressure and the other from the Dugdale adhesive stress. Hertz contact is assumed in the region
 . The contribution to the surface traction from the Hertz pressure is given by
. The contribution to the surface traction from the Hertz pressure is given by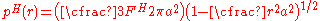
where the Hertz contact force
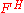 is given by
is given by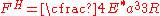
The penetration due to elastic compression is
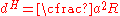
The vertical displacement at
 is
is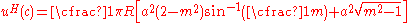
and the separation between the two surfaces at
 is
is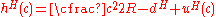
The surface traction distribution due to the adhesive Dugdale stress is
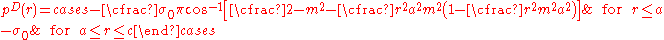
The total adhesive force is then given by
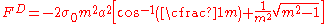
The compression due to Dugdale adhesion is
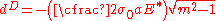
and the gap at
 is
is
The net traction on the contact area is then given by
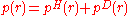 and the net contact force is
and the net contact force is 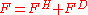 . When
. When  the adhesive traction drops to zero.
the adhesive traction drops to zero.Non-dimensionalized values of
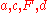 are introduced at this stage that are defied as
are introduced at this stage that are defied as
In addition, Maugis proposed a parameter
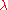 which is equivalent to the Tabor coefficient. This parameter is defined as
which is equivalent to the Tabor coefficient. This parameter is defined as
Then the net contact force may be expressed as
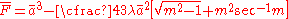
and the elastic compression as
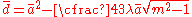
The equation for the cohesive gap between the two bodies takes the form

This equation can be solved to obtain values of
 for various values of
for various values of  and
and  . For large values of
. For large values of  ,
,  and the JKR model is obtained. For small values of
and the JKR model is obtained. For small values of 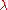 the DMT model is retrieved.
the DMT model is retrieved.Carpick-Ogletree-Salmeron (COS) model
The Maugis-Dugdale model can only be solved iteratively if the value of is not known a-priori. The Carpick-Ogletree-Salmeron approximate solution simplifies the process by using the following relation to determine the contact radius
is not known a-priori. The Carpick-Ogletree-Salmeron approximate solution simplifies the process by using the following relation to determine the contact radius  :
: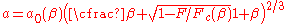
where
 is the contact area at zero load, and
is the contact area at zero load, and 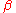 is a transition parameter that is related to
is a transition parameter that is related to 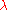 by
by
The case
 corresponds exactly to JKR theory while
corresponds exactly to JKR theory while  corresponds to DMT theory.
corresponds to DMT theory.For intermediate cases
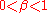 the COS model corresponds closely to the Maugis-Dugdale solution for
the COS model corresponds closely to the Maugis-Dugdale solution for  .
.See also
- AdhesiveAdhesiveAn adhesive, or glue, is a mixture in a liquid or semi-liquid state that adheres or bonds items together. Adhesives may come from either natural or synthetic sources. The types of materials that can be bonded are vast but they are especially useful for bonding thin materials...
- Adhesive bondingAdhesive bondingAdhesive bonding describes a wafer bonding technique with applying an intermediate layer to connect substrates of different materials. These produced connections can be soluble or insoluble. The commercially available adhesive can be organic or inorganic and is deposited on one or both substrate...
- Adhesive dermatitis
- Adhesive surface forces
- Bearing capacityBearing capacityIn geotechnical engineering, bearing capacity is the capacity of soil to support the loads applied to the ground. The bearing capacity of soil is the maximum average contact pressure between the foundation and the soil which should not produce shear failure in the soil...
- BioadhesivesBioadhesivesBioadhesives are natural polymeric materials that act as adhesives. The term is sometimes used more loosely to describe a glue formed synthetically from biological monomers such as sugars, or to mean a synthetic material designed to adhere to biological tissue....
- Contact dynamicsContact dynamicsContact dynamics deals with the motion of multibody systems subjected to unilateral contacts and friction. Such systems are omnipresent in many multibody dynamics applications...
- Dispersive adhesionDispersive adhesionDispersive adhesion, also called adsorptive adhesion, is a mechanism for adhesion which attributes attractive forces between two materials to intermolecular interactions between molecules of each material...
- Electrostatic generatorElectrostatic generatorAn electrostatic generator, or electrostatic machine, is a mechanical device that produces static electricity, or electricity at high voltage and low continuous current...
- Frictional contact mechanicsFrictional contact mechanicsContact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction...
- GallingGallingGalling usually refers to the adhesive wear and transfer of material between metallic surfaces in relative converging contact during sheet metal forming and other industrial operations....
- GoniometerGoniometerA goniometer is an instrument that either measures an angle or allows an object to be rotated to a precise angular position. The term goniometry is derived from two Greek words, gōnia, meaning angle, and metron, meaning measure....
- Non-smooth mechanicsNon-smooth mechanicsNon-smooth mechanics is a modeling approach in mechanics which does not require the time evolutions of the positions and of the velocities to be smooth functions anymore. Due to possible impacts, the velocities of the mechanical system are even allowed to undergo jumps at certain time instants in...
- Plastic wrapPlastic wrapPlastic wrap, cling film , cling wrap or food wrap, is a thin plastic film typically used for sealing food items in containers to keep them fresh over a longer period of time...
- Shock (mechanics)Shock (mechanics)A mechanical or physical shock is a sudden acceleration or deceleration caused, for example, by impact, drop, kick, earthquake, or explosion. Shock is a transient physical excitation....
- Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
- Surface tensionSurface tensionSurface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
- Synthetic setaeSynthetic setaeSynthetic setae emulate the setae found on the toes of a gecko and scientific research in this area is driven towards the development of dry adhesives. Geckos have no difficulty mastering vertical walls and are apparently capable of adhering themselves to just about any surface...
- Unilateral contactUnilateral contactIn mechanics, a unilateral contact denotes a mechanical constraint which prevents penetration between two bodies; see figure 1a. These bodies may be rigid or flexible...
- WettingWettingWetting is the ability of a liquid to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. The degree of wetting is determined by a force balance between adhesive and cohesive forces.Wetting is important in the bonding or adherence of...
External links
- http://gltrs.grc.nasa.gov/reports/1997/TM-107440.pdf: More about contact stresses and the evolution of bearing stress equations can be found in this publication by NASA Glenn Research Center head the NASA Bearing, Gearing and Transmission Section, Erwin Zaretsky.

