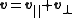Tangential and normal components
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
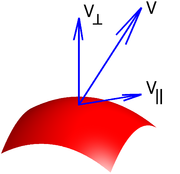
, given a vector at a point on a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
, that vector can be decomposed uniquely as a sum of two vectors, one tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the curve, called the tangential component of the vector, and another one perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the curve, called the normal component of the vector. Similarly a vector at a point on a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
can be broken down the same way.
More generally, given a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
N of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M, and a vector in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at a point of N, it can be decomposed into the component tangent to N and the component normal to N.
Surface
More formally, let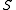 be a surface, and
be a surface, and  be a point on the surface. Let
be a point on the surface. Let  be a vector at
be a vector at 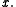 Then one can write uniquely
Then one can write uniquely  as a sum
as a sumwhere the first vector in the sum is the tangential component and the second one is the normal component. It follows immediately that these two vectors are perpendicular to each other.
To calculate the tangential and normal components, consider a unit normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the surface, that is, a unit vector
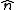 perpendicular to
perpendicular to 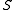 at
at 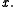 Then,
Then,
and thus
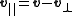
where "
 " denotes the dot product
" denotes the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. Another formula for the tangential component is
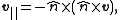
where "
 " denotes the cross product
" denotes the cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
.
Note that these formulas do not depend on the particular unit normal
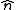 used (there exist two unit normals to any surface at a given point, pointing in opposite directions, so one of the unit normals is the negative of the other one).
used (there exist two unit normals to any surface at a given point, pointing in opposite directions, so one of the unit normals is the negative of the other one).Submanifold
More generally, given a submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
N of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M and
a point
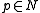 , we get a short exact sequence
, we get a short exact sequenceinvolving the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s:
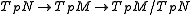
The quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
 is a generalized space of normal vectors.
is a generalized space of normal vectors.If M is a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, the above sequence splits, and the tangent space of M at p decomposes as a direct sum of the component tangent to N and the component normal to N:
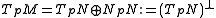
Thus every tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
 splits as
splits as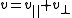 ,
,where
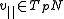 and
and 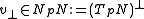 .
.Computations
Suppose N is given by non-degenerate equations.If N is given explicitly, via parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s (such as a parametric curve), then the derivative gives a spanning set for the tangent bundle (it's a basis if and only if the parametrization is an immersion).
If N is given implicitly (as in the above description of a surface, or more generally as a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
) as a level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
or intersection of level surfaces for
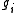 , then the gradients of
, then the gradients of 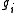 span the normal space.
span the normal space.In both cases, we can again compute using the dot product; the cross product is special to 3 dimensions though.
Applications
- Lagrange multipliersLagrange multipliersIn mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
: constrained critical pointsCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
are where the tangential component of the total derivativeTotal derivativeIn the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
vanish. - Surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...