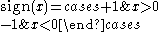
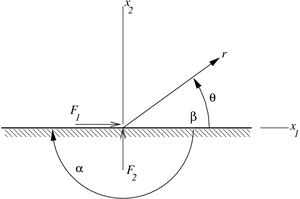
The Flamant solution provides expressions for the stresses

Stress (physics)

In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...

 and displacements

Displacement field (mechanics)

A displacement field is an assignment of displacement vectors for all points in a region or body that is displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position...

 in a linear elastic

Linear elasticity

Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...

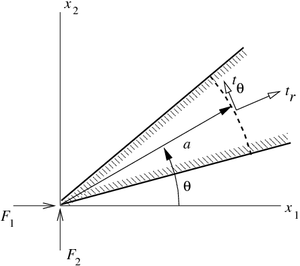
 wedge

Wedge (geometry)

In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes....

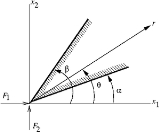
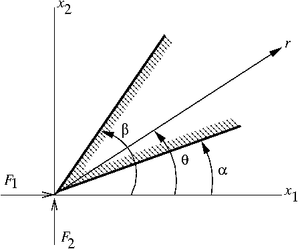
 loaded by point forces at its sharp end. This solution was developed by A. Flamant in 1892 by modifying the three-dimensional solution of Boussinesq

Linear elasticity

Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...

.

The stresses predicted by the Flamant solution are (in polar coordinates)
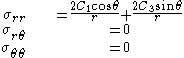
where are constants that are determined from the boundary conditions and the geometry of the wedge (i.e., the angles ) and satisfy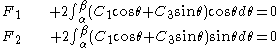
where 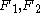are the applied forces.

The wedge problem is self-similar and has no inherent length scale. Also, all quantities can be expressed in the separated-variable form 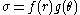. The stresses vary as .

Forces acting on a half-plane

For the special case where , , the wedge is converted into a half-plane with a normal force and a tangential force. In that case
Therefore the stresses are
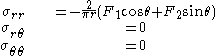
and the displacements are (using Michell's solution

Michell solution

The Michell solution is a general solution to the elasticity equations in polar coordinates . The solution is such that the stress components are in the form of a Fourier series in \theta \, ....

)
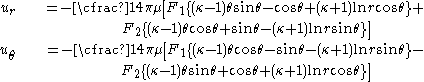
The 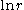dependence of the displacements implies that the displacement grows the further one moves from the point of application of the force (and is unbounded at infinity). This feature of the Flamant solution is confusing and appears unphysical. For a discussion of the issue see http://imechanica.org/node/319.

Displacements at the surface of the half-plane

The displacements in the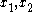 directions at the surface of the half-plane are given by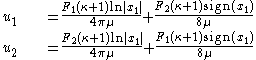
where
is the Poisson's ratio

Poisson's ratio

Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....

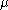, is the shear modulus, and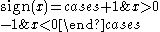

Derivation of Flamant solution

If we assume the stresses to vary as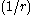 , we can pick terms containing in the stresses from Michell's solution

Michell solution

The Michell solution is a general solution to the elasticity equations in polar coordinates . The solution is such that the stress components are in the form of a Fourier series in \theta \, ....

. Then the Airy stress function can be expressed as
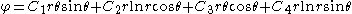
Therefore, from the tables in Michell's solution

Michell solution

The Michell solution is a general solution to the elasticity equations in polar coordinates . The solution is such that the stress components are in the form of a Fourier series in \theta \, ....

, we have
The constants 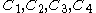can then, in principle, be determined from the wedge geometry and the applied boundary conditions.

However, the concentrated loads at the vertex are difficult to express in terms of traction boundary conditions because

1. the unit outward normal at the vertex is undefined
2. the forces are applied at a point (which has zero area) and hence the traction at that point is infinite.

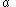To get around this problem, we consider a bounded region of the wedge and consider equilibrium of the bounded wedge. Let the bounded wedge have two traction free surfaces and a third surface in the form of an arc of a circle with radius . Along the arc of the circle, the unit outward normal is 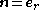where the basis vectors are 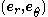. The tractions on the arc are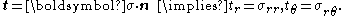

Next, we examine the force and moment equilibrium in the bounded wedge and get
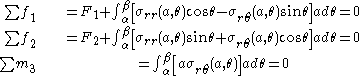
We require that these equations be satisfied for all values of 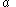and thereby satisfy the boundary conditions.

The traction-free boundary conditions on the edges 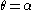and 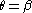also imply that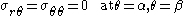
except at the point .

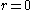If we assume that everywhere, then the traction-free conditions and the moment equilibrium equation are satisfied and we are left with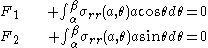
and 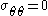along 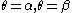except at the point 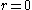. But the field 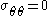everywhere also satisfies the force equilibrium equations. Hence this must be the solution. Also, the assumption 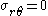implies that .

Therefore,

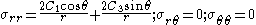
To find a particular solution for 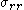we have to plug in the expression for 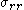into the force equilibrium equations to get a system of two equations which have to be solved for :

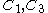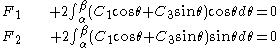
Forces acting on a half-plane

If we take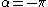 and 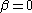, the problem is converted into one where a normal force 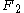and a tangential force 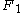act on a half-plane. In that case, the force equilibrium equations take the form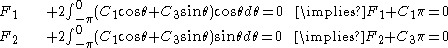
Therefore
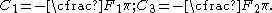
The stresses for this situation are
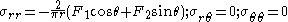
Using the displacement tables from the Michell solution

Michell solution

The Michell solution is a general solution to the elasticity equations in polar coordinates . The solution is such that the stress components are in the form of a Fourier series in \theta \, ....

, the displacements for this case are given by

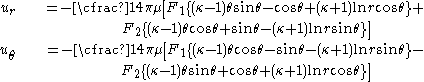
Displacements at the surface of the half-plane

To find expressions for the displacements at the surface of the half plane, we first find the displacements for positive (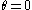) and negative 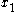() keeping in mind that 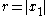along these locations.

For 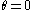we have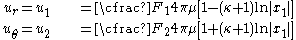
For 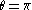we have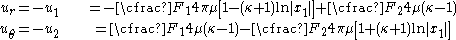
We can make the displacements symmetric around the point of application of the force by adding rigid body displacements (which does not affect the stresses)
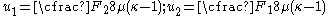
and removing the redundant rigid body displacements
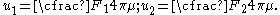
Then the displacements at the surface can be combined and take the form
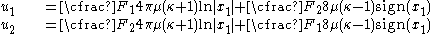
where