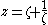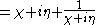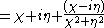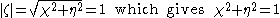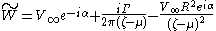Joukowsky transform
Encyclopedia
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, the Joukowsky transform, named after Nikolai Zhukovsky, is a conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
historically used to understand some principles of airfoil
Airfoil
An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....
design.
The transform is
where
is a complex variableComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
in the new space and
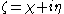is a complex variable in the original space.This transform is also called the Joukowsky transformation, the Joukowski transform, the Zhukovsky transform and other variations.
In aerodynamics
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
, the transform is used to solve for the two-dimensional potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
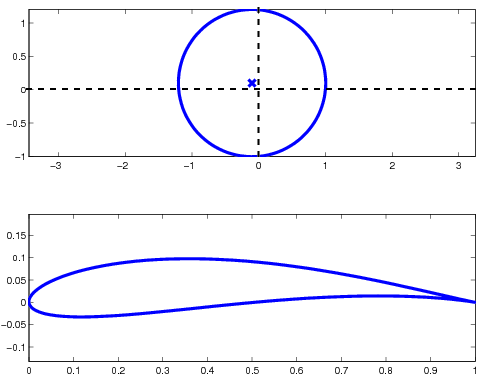
around a class of airfoils known as Joukowsky airfoils. A Joukowsky airfoil is generated in the z plane by applying the Joukowsky transform to a circle in the
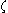plane. The coordinates of the centre of the circle are variables, and varying them modifies the shape of the resulting airfoil. The circle encloses the point 
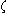=-1 (where the derivative is zero) and intersects the point 
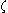= 1. This can be achieved for any allowable centre position 
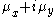by varying the radius of the circle.Joukowsky airfoils have a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
at their trailing edge
Trailing edge
The trailing edge of an aerodynamic surface such as a wing is its rear edge, where the airflow separated by the leading edge rejoins. Essential control surfaces are attached here to redirect the air flow and exert a controlling force by changing its momentum...
. A closely related conformal mapping, the Kármán-Trefftz Transform, generates the much broader class of Kármán-Trefftz Airfoils by controlling the trailing edge angle. When a trailing edge angle of zero is specified, the Kármán-Trefftz Transform reduces to generate the Joukowsky Airfoils.
General Joukowsky Transformation
The Joukowsky Transformation of any complex number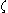
to 
is as follows
So the real component has
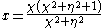
and imaginary component has
Sample Joukowsky Airfoil
The transformation of all complex numbers on the unit circle is a special case.
So the real component becomes
and the imaginary component becomes
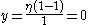
Thus the complex unit circle maps to a flat plate on the real number line from -2 to 2.
Transformation from other circles make a wide range of airfoil shapes.
Velocity field and circulation for the Joukowsky airfoil
The solution to potential flow around a circular cylinderPotential flow around a circular cylinder
In mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity...
is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
and well known. It is the superposition of uniform flow, a doublet, and a vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
.
The complex velocity
around the circle in the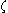 
plane is
where
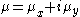is the complex coordinate of the centre of the circle
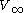is the freestream velocity of the fluid
is the angle of attackAngle of attackAngle of attack is a term used in fluid dynamics to describe the angle between a reference line on a lifting body and the vector representing the relative motion between the lifting body and the fluid through which it is moving...
of the airfoil with respect to the freestream flow- R is the radius of the circle, calculated using
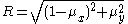
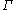is the circulation, found using the Kutta conditionKutta conditionThe Kutta condition is a principle in steady flow fluid dynamics, especially aerodynamics, that is applicable to solid bodies which have sharp corners such as the trailing edges of airfoils...
, which reduces in this case to
The complex velocity W around the airfoil in the z plane is, according to the rules of conformal mapping and using the Joukowsky transformation:
Here
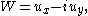with 
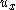and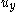 
the velocity components in the 
and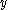 
directions, respectively (
with 
and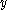 
real-valued).From this velocity, other properties of interest of the flow, such as the coefficient of pressure or lift
Lift (force)
A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction...
can be calculated.
A Joukowsky airfoil has a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
at the trailing edge.
The transformation is named after Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n scientist Nikolai Zhukovsky. His name has historically been romanized in a number of ways, thus the variation in spelling of the transform.
Kármán–Trefftz transform
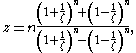(A)with n slightly smaller than 2. The angle α, between the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
s of the upper and lower airfoil surface, at the trailing edge is related to n by:
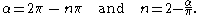
The derivative
, required to compute the velocity field, is equal to: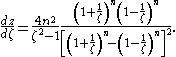
Background
First, add and subtract two from the Joukowsky transform, as given above:
Dividing the left and right hand sides gives:
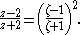
The right hand side contains (as a factor) the simple second-power law from potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory, applied at the trailing edge near
From conformal mapping theory this quadratic map is known to change a half plane in the 
-space into potential flow around a semi-infinite straight line. Further, values of the power less than two will result in flow around a finite angle. So, by changing the power in the Joukowsky transform — to a value slightly less than two — the result is a finite angle instead of a cusp. Replacing 2 by n in the previous equation gives: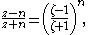
which is the Kármán–Trefftz transform. Solving for z gives it in the form of equation (A).