Penrose diagram
Encyclopedia
In theoretical physics
, a Penrose diagram (named for mathematical physicist Roger Penrose
) is a two-dimensional diagram
that captures the causal relations between different points in spacetime
. It is an extension of a Minkowski diagram
where the vertical dimension represents time
, and the horizontal
dimension represents space
, and slanted lines at an angle of 45° correspond to light rays. The biggest difference is that locally, the metric
on a Penrose diagram is conformally equivalent
to the actual metric in spacetime. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Penrose diagram of finite size. For spherically symmetric spacetime
s, every point in the diagram corresponds to a 2-sphere.
system of other space-time diagrams for local asymptotically flat spacetime
, it introduces a system of representing distant spacetime by shrinking or "crunching" distances that are further away. Straight lines of constant time and space coordinates therefore become hyperbola
s, which appear to converge at point
s in the corners of the diagram. These points represent "conformal infinity" for space and time.
Penrose diagrams are more properly (but less frequently) called Penrose-Carter diagrams (or Carter-Penrose diagrams), acknowledging both Brandon Carter
and Roger Penrose
, who were the first researchers to employ them. They are also called conformal diagrams, or simply spacetime diagrams.
Two lines drawn at 45° angles should intersect in the diagram only if the corresponding two light rays intersect in the actual spacetime.
So, a Penrose diagram can be used as a concise illustration of spacetime regions that are accessible to observation. The diagonal
boundary lines of a Penrose diagram correspond to the "infinity" or to singularities where light rays must end. Thus, Penrose diagrams are also useful in the study of asymptotic properties of spacetimes and singularities. An infinite static Minkowski universe
, coordinates
is related to Penrose coordinates 
by:
The corners of the Penrose diamond, which represent the spacelike and timelike conformal infinities, are
from the origin.
The singularity is represented by a spacelike boundary to make it clear that once an object has passed the horizon it will inevitably hit the singularity even if it attempts to take evasive action.
Penrose diagrams are also used to illustrate the space-time environment of a hypothetical wormhole
connecting two separate universes, which is an extension of the Schwarzschild solution of black hole
s. The precursors to the Penrose diagrams were Kruskal
-Szekeres
diagrams. These introduced the method of aligning the event horizon
into past and future horizons oriented at 45° angles (since one would need to travel faster than light to cross from the Schwarzschild radius
back into flat spacetime); and splitting the singularity
into past and future horizontally-oriented lines (since the singularity "cuts off" all paths into the future once one enters the hole).
The result is a hypothetical object called a grey hole, which is basically a white hole
that turns into a black hole
after briefly opening up into a wormhole connecting the two asymptotically flat space-time regions called "universes". The wormhole closes off (forming "future" singularities) so rapidly that passage between the two universes would require faster-than-light velocity, and is therefore impossible. The Penrose diagram simply added to Kruskal and Szekeres' diagram the conformal crunching of the regions of flat space-time far from the hole.
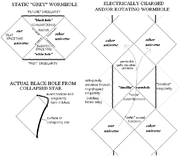While the basic space-like passage of a static black hole cannot be traversed, Penrose diagrams for rotating and/or electrically charged black holes reveal "inner event horizons" (lying in the future) and vertically oriented singularities, which open up what is known as a "time-like wormhole" allowing passage into future universes. In the case of the rotating hole, there is also a "negative gravity" universe entered through a ring-shaped singularity (still portrayed as a line in the diagram) that can be passed through if entering the hole close to its axis of rotation.
With all of this hypothesis regarding wormholes, some scientists have pointed out that
1) This does not describe a typical black hole created from the collapse of a star (which cuts off the past-oriented "white hole" geometry and other universe). Such wormholes would only be possible if a "past singularity" (such as a remnant of the original Big Bang
singularity that remained compact) continued erupting into the universe as time went on.
2) The radiation of orbiting, highly blue-shifted light rays surrounding a black hole (called a "blue sheet") would make it impossible for anyone to pass through, and in fact might create another kind of singularity outside the hole!
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a Penrose diagram (named for mathematical physicist Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
) is a two-dimensional diagram
Diagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
that captures the causal relations between different points in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. It is an extension of a Minkowski diagram
Minkowski diagram
The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
where the vertical dimension represents time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, and the horizontal
Horizontal plane
In geometry, physics, astronomy, geography, and related sciences, a plane is said to be horizontal at a given point if it is perpendicular to the gradient of the gravity field at that point— in other words, if apparent gravity makes a plumb bob hang perpendicular to the plane at that point.In...
dimension represents space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, and slanted lines at an angle of 45° correspond to light rays. The biggest difference is that locally, the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on a Penrose diagram is conformally equivalent
Conformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
to the actual metric in spacetime. The conformal factor is chosen such that the entire infinite spacetime is transformed into a Penrose diagram of finite size. For spherically symmetric spacetime
Spherically symmetric spacetime
A spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...
s, every point in the diagram corresponds to a 2-sphere.
Basic properties
While Penrose diagrams share the same basic coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
system of other space-time diagrams for local asymptotically flat spacetime
Asymptotically flat spacetime
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime....
, it introduces a system of representing distant spacetime by shrinking or "crunching" distances that are further away. Straight lines of constant time and space coordinates therefore become hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s, which appear to converge at point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s in the corners of the diagram. These points represent "conformal infinity" for space and time.
Penrose diagrams are more properly (but less frequently) called Penrose-Carter diagrams (or Carter-Penrose diagrams), acknowledging both Brandon Carter
Brandon Carter
Brandon Carter, FRS is an Australian theoretical physicist, best known for his work on the properties of black holes and for being the first to name and employ the anthropic principle in its contemporary form. He is a researcher at the Meudon campus of the Laboratoire Univers et Théories, part of...
and Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
, who were the first researchers to employ them. They are also called conformal diagrams, or simply spacetime diagrams.
So, a Penrose diagram can be used as a concise illustration of spacetime regions that are accessible to observation. The diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
boundary lines of a Penrose diagram correspond to the "infinity" or to singularities where light rays must end. Thus, Penrose diagrams are also useful in the study of asymptotic properties of spacetimes and singularities. An infinite static Minkowski universe
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, coordinates
is related to Penrose coordinates by:The corners of the Penrose diamond, which represent the spacelike and timelike conformal infinities, are
from the origin.Black holes
Penrose diagrams are frequently used to illustrate the space-time environment of black holes. Singularities are denoted by a spacelike boundary, unlike the timelike boundary found on conventional space-time diagrams. This is due to the interchanging of timelike and spacelike coordinates within the horizon of a black hole (since space is uni-directional within the horizon, just as time is uni-directional outside the horizon).The singularity is represented by a spacelike boundary to make it clear that once an object has passed the horizon it will inevitably hit the singularity even if it attempts to take evasive action.
Penrose diagrams are also used to illustrate the space-time environment of a hypothetical wormhole
Wormhole
In physics, a wormhole is a hypothetical topological feature of spacetime that would be, fundamentally, a "shortcut" through spacetime. For a simple visual explanation of a wormhole, consider spacetime visualized as a two-dimensional surface. If this surface is folded along a third dimension, it...
connecting two separate universes, which is an extension of the Schwarzschild solution of black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s. The precursors to the Penrose diagrams were Kruskal
Kruskal
Kruskal may refer to any of the following, of whom the first three are brothers:* William Kruskal , American mathematician and statistician** Kruskal–Wallis one-way analysis of variance, named after William Kruskal...
-Szekeres
Kruskal-Szekeres coordinates
In general relativity Kruskal–Szekeres coordinates, named for Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole...
diagrams. These introduced the method of aligning the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
into past and future horizons oriented at 45° angles (since one would need to travel faster than light to cross from the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
back into flat spacetime); and splitting the singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
into past and future horizontally-oriented lines (since the singularity "cuts off" all paths into the future once one enters the hole).
The result is a hypothetical object called a grey hole, which is basically a white hole
White hole
A white hole, in general relativity, is a hypothetical region of spacetime which cannot be entered from the outside, but from which matter and light may escape. In this sense it is the reverse of a black hole, which can be entered from the outside, but from which nothing, including light, may escape...
that turns into a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
after briefly opening up into a wormhole connecting the two asymptotically flat space-time regions called "universes". The wormhole closes off (forming "future" singularities) so rapidly that passage between the two universes would require faster-than-light velocity, and is therefore impossible. The Penrose diagram simply added to Kruskal and Szekeres' diagram the conformal crunching of the regions of flat space-time far from the hole.
With all of this hypothesis regarding wormholes, some scientists have pointed out that
1) This does not describe a typical black hole created from the collapse of a star (which cuts off the past-oriented "white hole" geometry and other universe). Such wormholes would only be possible if a "past singularity" (such as a remnant of the original Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
singularity that remained compact) continued erupting into the universe as time went on.
2) The radiation of orbiting, highly blue-shifted light rays surrounding a black hole (called a "blue sheet") would make it impossible for anyone to pass through, and in fact might create another kind of singularity outside the hole!
See also
- CausalityCausalityCausality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
- Weyl transformation
- Causal structureCausal structureIn mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
- Conformal cyclic cosmologyConformal Cyclic CosmologyThe Conformal Cyclic Cosmology is a cosmological model in the framework of general relativity, advanced by the theoretical physicist Sir Roger Penrose. In CCC, the universe iterates through infinite cycles, with the future timelike infinity of each previous iteration being identified with the Big...