
Stream function
Encyclopedia
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential
lines. In most cases, the stream function is the imaginary part of the complex potential, while the potential function is the real part.
Considering the particular case of fluid dynamics
, the difference between the stream function values at any two points gives the volumetric flow rate (or volumetric flux
) through a line connecting the two points.
Since streamlines are tangent
to the velocity vector of the flow, the value of the stream function must be constant along a streamline. If there were a flux across a line, it would necessarily not be tangent to the flow, hence would not be a streamline.
The usefulness of the stream function lies in the fact that the velocity components in the x- and y- directions at a given point are given by the partial derivative
s of the stream function at that point. A stream function may be defined for any flow of dimensions greater than or equal to two, however the two dimensional case is generally the easiest to visualize and derive.
Taken together with the velocity potential, the stream function may be used to derive a complex potential
for a potential flow
. In other words, the stream function accounts for the solenoidal part of a two-dimensional Helmholtz decomposition
, while the velocity potential accounts for the irrotational part.
One way is to define the stream function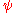 for a two dimensional flow such that the flow velocity
for a two dimensional flow such that the flow velocity
can be expressed as: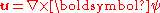
Where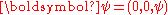 if the velocity vector
if the velocity vector 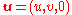 .
.
In Cartesian coordinate system
this is equivalent to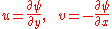
Where and
and  are the velocities in the
are the velocities in the  and
and 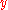 coordinate directions, respectively.
coordinate directions, respectively.
 ,
,
where is a unit vector in the
is a unit vector in the  direction and the subscripts indicate partial derivatives.
direction and the subscripts indicate partial derivatives.
Note that this definition has the opposite sign to that given above (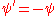 ), so we have
), so we have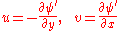
in Cartesian coordinates.
Both formulations of the stream function constrain the velocity to satisfy the two dimensional continuity equation
exactly: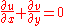

As δn → 0, rearranging this expression, we get: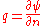
Now consider two dimensional plane flow with reference to a coordinate system. Suppose an observer looks along an arbitrary axis in the direction of increase and sees flow crossing the axis from left to right. A sign convention is adopted such that the velocity of the flow is positive.

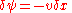
where u is the velocity parallel to and in the direction of the x-axis, and v is the velocity parallel to and in the direction of the y-axis. Thus, as δn → 0 and by rearranging, we have: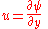
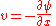
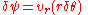
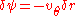
where vr is the radial velocity component (parallel to the r-axis), and vθ is the tangential velocity component (parallel to the θ-axis). Thus, as δn → 0 and by rearranging, we have:
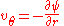
states that if we consider incompressible flow into an elemental square, the flow into that small element must equal the flow out of that element.
The total flow into the element is given by: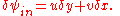
The total flow out of the element is given by: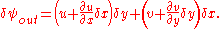
Thus we have:
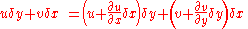
and simplifying to:
Substituting the expressions of the stream function into this equation, we have:
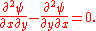
:
or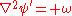
where and
and 
Equipotential
Equipotential or isopotential in mathematics and physics refers to a region in space where every point in it is at the same potential. This usually refers to a scalar potential , although it can also be applied to vector potentials...
lines. In most cases, the stream function is the imaginary part of the complex potential, while the potential function is the real part.
Considering the particular case of fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the difference between the stream function values at any two points gives the volumetric flow rate (or volumetric flux
Volumetric flux
In fluid dynamics, the volumetric flux is the rate of volume flow across a unit area . The density of a particular property in a fluid's volume, multiplied with the volumetric flux of the fluid, thus defines the advective flux of that property...
) through a line connecting the two points.
Since streamlines are tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the velocity vector of the flow, the value of the stream function must be constant along a streamline. If there were a flux across a line, it would necessarily not be tangent to the flow, hence would not be a streamline.
The usefulness of the stream function lies in the fact that the velocity components in the x- and y- directions at a given point are given by the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the stream function at that point. A stream function may be defined for any flow of dimensions greater than or equal to two, however the two dimensional case is generally the easiest to visualize and derive.
Taken together with the velocity potential, the stream function may be used to derive a complex potential
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
for a potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
. In other words, the stream function accounts for the solenoidal part of a two-dimensional Helmholtz decomposition
Helmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
, while the velocity potential accounts for the irrotational part.
Definitions
The sign of the stream function depends on the definition used.One way is to define the stream function
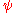 for a two dimensional flow such that the flow velocity
for a two dimensional flow such that the flow velocityFlow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
can be expressed as:
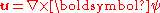
Where
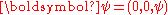 if the velocity vector
if the velocity vector 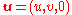 .
.In Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
this is equivalent to
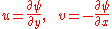
Where
 and
and  are the velocities in the
are the velocities in the  and
and 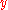 coordinate directions, respectively.
coordinate directions, respectively.Alternative definition (opposite sign)
Another definition (used more widely in meteorology and oceanography than the above) is ,
,where
 is a unit vector in the
is a unit vector in the  direction and the subscripts indicate partial derivatives.
direction and the subscripts indicate partial derivatives.Note that this definition has the opposite sign to that given above (
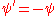 ), so we have
), so we have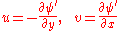
in Cartesian coordinates.
Both formulations of the stream function constrain the velocity to satisfy the two dimensional continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
exactly:
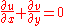
Derivation of the two dimensional stream function
Consider two points A and B in two dimensional plane flow. If the distance between these two points is very small: δn, and a stream of flow passes between these points with an average velocity, q perpendicular to the line AB, the volume flow rate per unit thickness, δΨ is given by:
As δn → 0, rearranging this expression, we get:
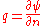
Now consider two dimensional plane flow with reference to a coordinate system. Suppose an observer looks along an arbitrary axis in the direction of increase and sees flow crossing the axis from left to right. A sign convention is adopted such that the velocity of the flow is positive.
Flow in Cartesian coordinates
By observing the flow into an elemental square in an x-y Cartesian coordinate system, we have:
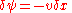
where u is the velocity parallel to and in the direction of the x-axis, and v is the velocity parallel to and in the direction of the y-axis. Thus, as δn → 0 and by rearranging, we have:
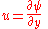
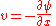
Flow in Polar coordinates
By observing the flow into an elemental square in an r-θ Polar coordinate system, we have: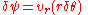
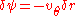
where vr is the radial velocity component (parallel to the r-axis), and vθ is the tangential velocity component (parallel to the θ-axis). Thus, as δn → 0 and by rearranging, we have:

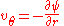
Continuity: The Derivation
Consider two dimensional plane flow within a Cartesian coordinate system. ContinuityContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
states that if we consider incompressible flow into an elemental square, the flow into that small element must equal the flow out of that element.
The total flow into the element is given by:
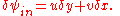
The total flow out of the element is given by:
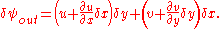
Thus we have:

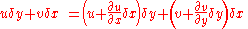
and simplifying to:

Substituting the expressions of the stream function into this equation, we have:
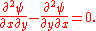
Vorticity
In Cartesian coordinates, the stream function can be found from vorticity using the following Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:

or
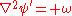
where
 and
and 

