.gif)
Dispersion (water waves)
Encyclopedia
In fluid dynamics
, dispersion of water waves
generally refers to frequency dispersion
, which means that wave
s of different wavelength
s travel at different phase speeds. Water waves, in this context, are waves propagating on the water
surface
, and forced by gravity
and surface tension
. As a result, water with a free surface
is generally considered to be a dispersive medium
.
Surface gravity waves, moving under the forcing by gravity, propagate faster for increasing wavelength
. For a given wavelength, gravity waves in deeper water have a larger phase speed than in shallower water
. In contrast with this, capillary wave
s only forced by surface tension, propagate faster for shorter wavelengths.
Besides frequency dispersion, water waves also exhibit amplitude dispersion. This is a nonlinear effect, by which waves of larger amplitude
have a different phase speed from small-amplitude waves.
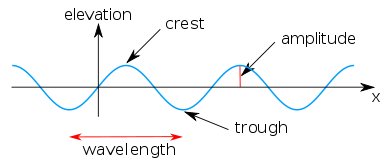 The simplest propagating wave
The simplest propagating wave
of unchanging form is a sine wave
. A sine wave with water surface elevation
η( x, t ) is given by:

where a is the amplitude
(in metres) and θ = θ( x, t ) is the phase function (in radian
s), depending on the horizontal position ( x , in metres) and time ( t , in second
s):
 with
with  and
and 
where:
Characteristic phases of a water wave are:
A certain phase repeats itself after an integer
m multiple of 2π: sin(θ) = sin(θ+m•2π).
Essential for water waves, and other wave phenomena in physics
, is that free propagating waves of non-zero amplitude only exist when the angular frequency ω and wavenumber k (or equivalently the wavelength λ and period T ) satisfy a functional relationship
: the frequency dispersion relation

The dispersion relation has two solutions: ω = +Ω(k) and ω = -Ω(k), corresponding to waves travelling in the positive or negative x–direction. The dispersion relation will in general depend on several other parameters in addition to the wavenumber k. For gravity waves, according to linear theory, these are the acceleration by gravity
and the water depth.
An initial wave phase θ = θ0 propagates as a function of space and time. Its subsequent position is given by:

This shows that the phase moves with the velocity:

which is called the phase velocity.
A sinusoidal wave, of small surface-elevation amplitude
and with a constant wavelength
, propagates with the phase velocity
, also called celerity or phase speed. While the phase velocity is a vector and has an associated direction, celerity or phase speed refer only to the magnitude of the phase velocity. According to linear theory for waves forced by gravity, the phase speed depends on the wavelength and the water depth. For a fixed water depth, long waves (with large wavelength) propagate faster than shorter waves.
In the left figure, it can be seen that shallow water
waves, with wavelengths λ much larger than the water depth h, travel with the phase velocity

with g the acceleration by gravity
and cp the phase speed. Since this shallow-water phase speed is independent of the wavelength, shallow water waves do not have frequency dispersion.
Using another normalization for the same frequency dispersion relation, the figure on the right shows that in deep water, with water depth h larger than half the wavelength λ (so for h/λ > 0.5), the phase velocity cp is independent of the water depth:

with T the wave period
(the reciprocal
of the frequency
f, T=1/f ). So in deep water the phase speed increases with the wavelength, and with the period.
Since the phase speed satisfies cp = λ/T = λf, wavelength and period (or frequency) are related. For instance in deep water:

The dispersion characteristics for intermediate depth are given below.
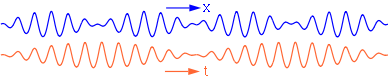
 Interference of two sinusoidal waves with slightly different wavelengths, but the same amplitude
Interference of two sinusoidal waves with slightly different wavelengths, but the same amplitude
and propagation direction, results in a beat pattern
, called a wave group. As can be seen in the animation, the group moves with a group velocity cg different from the phase velocity cp, due to frequency dispersion.
The group velocity is depicted by the red lines (marked B) in the two figures above.
In shallow water, the group velocity is equal to the shallow-water phase velocity. This is because shallow water waves are not dispersive. In deep water, the group velocity is equal to half the phase velocity: cg = ½ cp.
The group velocity also turns out to be the energy transport velocity. This is the velocity with which the mean wave energy is transported horizontally in a narrow-band
wave field.
In case of a the group velocity different from the phase velocity, a consequence is that the number of waves counted in a wave group is different when counted from a snapshot in space at a certain moment, from when counted in time from the measured surface elevation at a fixed position. Consider a wave group of length Λg and group duration of τg. The group velocity is:

 The number of waves in a wave group, measured in space at a certain moment is: Λg / λ. While measured at a fixed location in time, the number of waves in a group is: τg / T. So the ratio of the number of waves measured in space to those measured in time is:
The number of waves in a wave group, measured in space at a certain moment is: Λg / λ. While measured at a fixed location in time, the number of waves in a group is: τg / T. So the ratio of the number of waves measured in space to those measured in time is:

So in deep water, with cg = ½ cp, a wave group has twice as many waves in time as it has in space.
The water surface elevation η(x,t), as a function of horizontal position x and time t, for a bichromatic wave group of full modulation
can be mathematically
formulated as:

with:
Both ω1 and k1, as well as ω2 and k2, have to satisfy the dispersion relation:
 and
and 
Using trigonometric identities, the surface elevation is written as:

The part between square brackets is the slowly-varying amplitude of the group, with group wave number ½ ( k1 - k2 ) and group angular frequency ½ ( ω1 - ω2 ). As a result, the group velocity is, for the limit k1 → k2 :

Wave groups can only be discerned in case of a narrow-banded signal, with the wave-number difference k1 - k2 small compared to the mean wave number ½ (k1 + k2).
 The effect of frequency dispersion is that the waves travel as a function of wavelength, so that spatial and temporal phase properties of the propagating wave are constantly changing. For example, under the action of gravity, water waves with a longer wavelength
The effect of frequency dispersion is that the waves travel as a function of wavelength, so that spatial and temporal phase properties of the propagating wave are constantly changing. For example, under the action of gravity, water waves with a longer wavelength
travel faster than those with a shorter wavelength.
While two superimposed sinusoidal waves, called a bichromatic wave, have an envelope
which travels unchanged, three or more sinusoidal wave components result in a changing pattern of the waves and their envelope. A sea state
– that is: real waves on the sea or ocean – can be described as a superposition of many sinusoidal waves with different wavelengths, amplitudes, initial phases and propagation directions. Each of these components travels with its own phase velocity, in accordance with the dispersion relation. The statistics
of such a surface can be described by its power spectrum.
Deep water corresponds with water depths larger than half the wavelength
, which is the common situation in the ocean. In deep water, longer period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity
. In shallow water
, for wavelengths larger than twenty times the water depth, as found quite often near the coast, the group velocity is equal to the phase velocity.
, although there were some errors in his solution for the linear wave problem.
The complete theory for linear water waves, including dispersion, was derived by George Biddell Airy
and published in about 1840. A similar equation was also found by Philip Kelland
at around the same time (but making some mistakes in his derivation of the wave theory).
The shallow water (with small h / λ) limit, ω2 = gh k2, was derived by Joseph Louis Lagrange
.
 In case of gravity-capillary waves, where surface tension
In case of gravity-capillary waves, where surface tension
affects the waves, the dispersion relation becomes:
with σ the surface tension (in N/m).
): a single hump of water traveling with constant velocity in shallow water with a horizontal bed. The single soliton solution of the Korteweg–de Vries equation
, of wave height H in water depth h far away from the wave crest, travels with the velocity:

So for this nonlinear gravity wave it is the total water depth under the wave crest that determines the speed, with higher waves traveling faster than lower waves. Note that soliton solutions only exist for positive values of H, solitary gravity waves of depression do not exist.
expansion, with the orders in terms of the wave steepness k A (where A is wave amplitude
). To the third order, and for deep water, the dispersion relation is

This implies that large waves travel faster than small ones of the same frequency. This is only noticeable when the wave steepness k A is large.

with k the wavenumber. Then for a medium with mean velocity
vector V, the dispersion relationship with Doppler shift becomes:

where k is the wavenumber vector, related to k as: k = |k|. The inner product k•V is equal to: k•V = kV cos α, with V the length of the mean velocity vector V: V = |V|. And α the angle between the wave propagation direction and the mean flow direction. For waves and current in the same direction, k•V=kV.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, dispersion of water waves
Ocean surface wave
In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
generally refers to frequency dispersion
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
, which means that wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s of different wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s travel at different phase speeds. Water waves, in this context, are waves propagating on the water
Water
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, and forced by gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
and surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
. As a result, water with a free surface
Free surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
is generally considered to be a dispersive medium
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
.
Surface gravity waves, moving under the forcing by gravity, propagate faster for increasing wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. For a given wavelength, gravity waves in deeper water have a larger phase speed than in shallower water
Shallow water
Shallow water may refer to:* Shallow water blackout* Waves and shallow water** Shallow water equations** Boussinesq equations * Shallow Water, Kansas...
. In contrast with this, capillary wave
Capillary wave
A capillary wave is a wave traveling along the phase boundary of a fluid, whose dynamics are dominated by the effects of surface tension.Capillary waves are common in nature and the home, and are often referred to as ripples...
s only forced by surface tension, propagate faster for shorter wavelengths.
Besides frequency dispersion, water waves also exhibit amplitude dispersion. This is a nonlinear effect, by which waves of larger amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
have a different phase speed from small-amplitude waves.
Frequency dispersion for surface gravity waves
This section is about frequency dispersion for waves on a fluid layer forced by gravity, and according to linear theory.Wave propagation and dispersion

Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
of unchanging form is a sine wave
Sine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
. A sine wave with water surface elevation
Elevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
η( x, t ) is given by:

where a is the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
(in metres) and θ = θ( x, t ) is the phase function (in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s), depending on the horizontal position ( x , in metres) and time ( t , in second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s):
 with
with  and
and 
where:
- λ is the wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
(in metres), - T is the periodPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
(in seconds), - k is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
(in radians per metre) and - ω is the angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
(in radians per second).
Characteristic phases of a water wave are:
- the upward zero-crossing at θ = 0,
- the wave crestCrest (physics)A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
at θ = ½ π, - the downward zero-crossing at θ = π and
- the wave trough at θ = 1½ π.
A certain phase repeats itself after an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
m multiple of 2π: sin(θ) = sin(θ+m•2π).
Essential for water waves, and other wave phenomena in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, is that free propagating waves of non-zero amplitude only exist when the angular frequency ω and wavenumber k (or equivalently the wavelength λ and period T ) satisfy a functional relationship
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
: the frequency dispersion relation

The dispersion relation has two solutions: ω = +Ω(k) and ω = -Ω(k), corresponding to waves travelling in the positive or negative x–direction. The dispersion relation will in general depend on several other parameters in addition to the wavenumber k. For gravity waves, according to linear theory, these are the acceleration by gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
and the water depth.
An initial wave phase θ = θ0 propagates as a function of space and time. Its subsequent position is given by:

This shows that the phase moves with the velocity:

which is called the phase velocity.
Phase velocity
 |
 |
A sinusoidal wave, of small surface-elevation amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and with a constant wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, propagates with the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
, also called celerity or phase speed. While the phase velocity is a vector and has an associated direction, celerity or phase speed refer only to the magnitude of the phase velocity. According to linear theory for waves forced by gravity, the phase speed depends on the wavelength and the water depth. For a fixed water depth, long waves (with large wavelength) propagate faster than shorter waves.
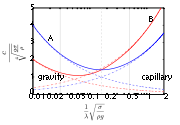
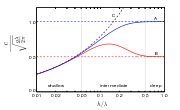
In the left figure, it can be seen that shallow water
Shallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
waves, with wavelengths λ much larger than the water depth h, travel with the phase velocity

with g the acceleration by gravity
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
and cp the phase speed. Since this shallow-water phase speed is independent of the wavelength, shallow water waves do not have frequency dispersion.
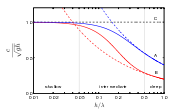
Using another normalization for the same frequency dispersion relation, the figure on the right shows that in deep water, with water depth h larger than half the wavelength λ (so for h/λ > 0.5), the phase velocity cp is independent of the water depth:

with T the wave period
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
(the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
f, T=1/f ). So in deep water the phase speed increases with the wavelength, and with the period.
Since the phase speed satisfies cp = λ/T = λf, wavelength and period (or frequency) are related. For instance in deep water:

The dispersion characteristics for intermediate depth are given below.
Group velocity

Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and propagation direction, results in a beat pattern
Beat (acoustics)
In acoustics, a beat is an interference between two sounds of slightly different frequencies, perceived as periodic variations in volume whose rate is the difference between the two frequencies....
, called a wave group. As can be seen in the animation, the group moves with a group velocity cg different from the phase velocity cp, due to frequency dispersion.
The group velocity is depicted by the red lines (marked B) in the two figures above.
In shallow water, the group velocity is equal to the shallow-water phase velocity. This is because shallow water waves are not dispersive. In deep water, the group velocity is equal to half the phase velocity: cg = ½ cp.
The group velocity also turns out to be the energy transport velocity. This is the velocity with which the mean wave energy is transported horizontally in a narrow-band
Narrowband
In radio, narrowband describes a channel in which the bandwidth of the message does not significantly exceed the channel's coherence bandwidth. It is a common misconception that narrowband refers to a channel which occupies only a "small" amount of space on the radio spectrum.The opposite of...
wave field.
In case of a the group velocity different from the phase velocity, a consequence is that the number of waves counted in a wave group is different when counted from a snapshot in space at a certain moment, from when counted in time from the measured surface elevation at a fixed position. Consider a wave group of length Λg and group duration of τg. The group velocity is:




So in deep water, with cg = ½ cp, a wave group has twice as many waves in time as it has in space.
The water surface elevation η(x,t), as a function of horizontal position x and time t, for a bichromatic wave group of full modulation
Modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
can be mathematically
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
formulated as:

with:
- a the wave amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of each frequency component in metres, - k1 and k2 the wave number of each wave component, in radians per metre, and
- ω1 and ω2 the angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of each wave component, in radians per second.
Both ω1 and k1, as well as ω2 and k2, have to satisfy the dispersion relation:
 and
and 
Using trigonometric identities, the surface elevation is written as:

The part between square brackets is the slowly-varying amplitude of the group, with group wave number ½ ( k1 - k2 ) and group angular frequency ½ ( ω1 - ω2 ). As a result, the group velocity is, for the limit k1 → k2 :

Wave groups can only be discerned in case of a narrow-banded signal, with the wave-number difference k1 - k2 small compared to the mean wave number ½ (k1 + k2).
Multi-component wave patterns

Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
travel faster than those with a shorter wavelength.
While two superimposed sinusoidal waves, called a bichromatic wave, have an envelope
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
which travels unchanged, three or more sinusoidal wave components result in a changing pattern of the waves and their envelope. A sea state
Sea state
In oceanography, a sea state is the general condition of the free surface on a large body of water—with respect to wind waves and swell—at a certain location and moment. A sea state is characterized by statistics, including the wave height, period, and power spectrum. The sea state varies with...
– that is: real waves on the sea or ocean – can be described as a superposition of many sinusoidal waves with different wavelengths, amplitudes, initial phases and propagation directions. Each of these components travels with its own phase velocity, in accordance with the dispersion relation. The statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
of such a surface can be described by its power spectrum.
Dispersion relation
In the table below, the dispersion relation ω2 = [Ω(k)]2 between angular frequency ω = 2π / T and wave number k = 2π / λ is given, as well as the phase and group speeds.| Frequency dispersion of gravity waves on the surface of deep water, shallow water and at intermediate depth, according to linear wave theory | |||||
|---|---|---|---|---|---|
| quantity | symbol | units | deep water( h > ½ λ ) | shallow water( h < 0.05 λ ) | intermediate depth( all λ and h ) |
| dispersion relation |  |
rad Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... / s |
 |
 |
 |
| phase velocity Phase velocity The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity... |
 |
m / s |  |
 |
 |
| group velocity Group velocity The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space.... |
 |
m / s |  |
 |
 |
| ratio |  |
- |  |
 |
 |
| wavelength |  |
m |  |
 |
for given period T, the solution of:  |
Deep water corresponds with water depths larger than half the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, which is the common situation in the ocean. In deep water, longer period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
. In shallow water
Waves and shallow water
When waves travel into areas of shallow water, they begin to be affected by the ocean bottom. The free orbital motion of the water is disrupted, and water particles in orbital motion no longer return to their original position. As the water becomes shallower, the swell becomes higher and steeper,...
, for wavelengths larger than twenty times the water depth, as found quite often near the coast, the group velocity is equal to the phase velocity.
History
The full linear dispersion relation was first found by Pierre-Simon LaplacePierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, although there were some errors in his solution for the linear wave problem.
The complete theory for linear water waves, including dispersion, was derived by George Biddell Airy
George Biddell Airy
Sir George Biddell Airy PRS KCB was an English mathematician and astronomer, Astronomer Royal from 1835 to 1881...
and published in about 1840. A similar equation was also found by Philip Kelland
Philip Kelland
Philip Kelland PRSE FRS was an English mathematician. He was known mainly for his great influence on the development of education in Scotland.-Early life:Kelland was born in 1808 in Dunster, Somerset, England...
at around the same time (but making some mistakes in his derivation of the wave theory).
The shallow water (with small h / λ) limit, ω2 = gh k2, was derived by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
.
Surface tension effects

Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
affects the waves, the dispersion relation becomes:

with σ the surface tension (in N/m).
Shallow water
Amplitude dispersion effects appear for instance in the solitary wave (or solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
): a single hump of water traveling with constant velocity in shallow water with a horizontal bed. The single soliton solution of the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
, of wave height H in water depth h far away from the wave crest, travels with the velocity:

So for this nonlinear gravity wave it is the total water depth under the wave crest that determines the speed, with higher waves traveling faster than lower waves. Note that soliton solutions only exist for positive values of H, solitary gravity waves of depression do not exist.
Deep water
The linear dispersion relation – unaffected by wave amplitude – is for nonlinear waves also correct at the second order of the perturbation theoryPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
expansion, with the orders in terms of the wave steepness k A (where A is wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
). To the third order, and for deep water, the dispersion relation is

This implies that large waves travel faster than small ones of the same frequency. This is only noticeable when the wave steepness k A is large.
Waves on a mean current: Doppler shift
Water waves on a mean flow (so a wave in a moving medium) experience a Doppler shift. Suppose the dispersion relation for a non-moving medium is:
with k the wavenumber. Then for a medium with mean velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
vector V, the dispersion relationship with Doppler shift becomes:

where k is the wavenumber vector, related to k as: k = |k|. The inner product k•V is equal to: k•V = kV cos α, with V the length of the mean velocity vector V: V = |V|. And α the angle between the wave propagation direction and the mean flow direction. For waves and current in the same direction, k•V=kV.
Dispersive water-wave models
- Airy wave theoryAiry wave theoryIn fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
- Benjamin–Bona–Mahony equation
- Boussinesq approximation (water waves)Boussinesq approximation (water waves)In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell of the wave of translation...
- Camassa-Holm equation
- Davey–Stewartson equations
- Kadomtsev–Petviashvili equation or KP equation
- Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(or KdV equation) - Luke's variational principleLuke's variational principleIn fluid dynamics, Luke's variational principle is a Lagrangian variational description of the motion of surface waves on a fluid with a free surface, under the action of gravity. This principle is named after J.C. Luke, who published it in 1967...
- Nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
- Shallow water equationsShallow water equationsThe shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
External links
- Mathematical aspects of dispersive waves are discussed on the Dispersive Wiki.

