
Collocation method
Encyclopedia
In mathematics, a collocation method is a method for the numerical
solution of ordinary differential equation
s, partial differential equation
s and integral equation
s. The idea is to choose a finite-dimensional space of candidate solutions (usually, polynomial
s up to a certain degree) and a number of points in the domain (called collocation points), and to select that solution which satisfies the given equation at the collocation points.
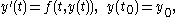
is to be solved over the interval [t0, t0 + h]. Choose 0 ≤ c1< c2< … < cn ≤ 1.
The corresponding (polynomial) collocation method approximates the solution y by the polynomial p of degree n which satisfies the initial condition p(t0) = y0, and the differential equation p' (t) = f(t,p(t)) at all points, called the collocation points, t = t0 + ckh where k = 1, …, n. This gives n + 1 conditions, which matches the n + 1 parameters needed to specify a polynomial of degree n.
All these collocation methods are in fact implicit Runge–Kutta methods
. However, not all implicit Runge–Kutta methods are collocation methods.
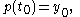


There are three conditions, so p should be a polynomial of degree 2. Write p in the form
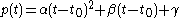
to simplify the computations. Then the collocation conditions can be solved to give the coefficients
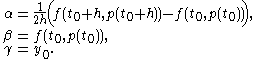
The collocation method is now given (implicitly) by

where y1 = p(t0 + h) is the approximate solution at t = t0 + h.
This method is known as the "trapezoidal rule." Indeed, this method can also be derived by rewriting the differential equation as
and approximating the integral on the right-hand side by the trapezoidal rule for integrals.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
solution of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s. The idea is to choose a finite-dimensional space of candidate solutions (usually, polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s up to a certain degree) and a number of points in the domain (called collocation points), and to select that solution which satisfies the given equation at the collocation points.
Ordinary differential equations
Suppose that the ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is to be solved over the interval [t0, t0 + h]. Choose 0 ≤ c1< c2< … < cn ≤ 1.
The corresponding (polynomial) collocation method approximates the solution y by the polynomial p of degree n which satisfies the initial condition p(t0) = y0, and the differential equation p
All these collocation methods are in fact implicit Runge–Kutta methods
Runge–Kutta methods
In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
. However, not all implicit Runge–Kutta methods are collocation methods.
Example
Pick, as an example, the two collocation points c1 = 0 and c2 = 1 (so n = 2). The collocation conditions are


There are three conditions, so p should be a polynomial of degree 2. Write p in the form
to simplify the computations. Then the collocation conditions can be solved to give the coefficients
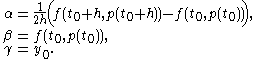
The collocation method is now given (implicitly) by

where y1 = p(t0 + h) is the approximate solution at t = t0 + h.
This method is known as the "trapezoidal rule." Indeed, this method can also be derived by rewriting the differential equation as
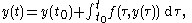
and approximating the integral on the right-hand side by the trapezoidal rule for integrals.

