
Spread polynomials
Encyclopedia
In the conventional language of trigonometry
, the nth-degree spread polynomial
Sn, for n = 0, 1, 2, ..., may be characterized by the trigonometric identity
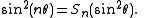
Although that is probably the simplest way to explain what spread polynomials are to those versed in well-known topics in mathematics, spread polynomials were introduced by Norman Wildberger for use in rational trigonometry
, a subject in which one generally avoids the sine
function and the other trigonometric functions of angles. The angle at which two lines meet is determined by a rational function
of their slopes, known as the spread between the two lines. The spread is equal to the square of the sine. The rational function can be identified without mentioning the sine function; see rational trigonometry
for more on this.
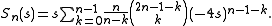 (S. Goh)
(S. Goh)
 (M. Hovdan)
(M. Hovdan)
From the definition it immediately follows that
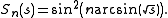
of the first kind, Tn by the identity
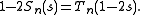
This implies
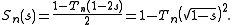
The second equality above follows from the identity
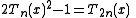
on Chebyshev polynomials.
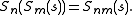
Fp, then the sequence { Sn }n = 0, 1, 2, ... of spread polynomials is periodic with period (p2 − 1)/2. In other words, if k = (p2 − 1)/2, then Sn + k = Sn, for all n.
, then for n ≠ m, we have
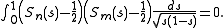
For n = m, the integral is π/8 unless n = m = 0, in which case it is π/4.
is
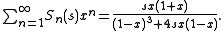
The exponential generating function is
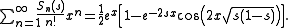
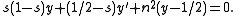
is a recently introduced approach to trigonometry that eschews all transcendental function
s (such as sine, cosine, etc.), all measurements of angles or compositions of rotations, and characterizes the separation between lines by a quantity called the "spread", which is a rational function
of the slopes. Equality of angles between rays entails equality of spreads between lines. The spread between two lines is the square of the sine of the angle. The name "spread polynomials" comes from the use of these polynomials in rational trigonometry.

Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, the nth-degree spread polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
Sn, for n = 0, 1, 2, ..., may be characterized by the trigonometric identity
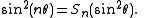
Although that is probably the simplest way to explain what spread polynomials are to those versed in well-known topics in mathematics, spread polynomials were introduced by Norman Wildberger for use in rational trigonometry
Rational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their...
, a subject in which one generally avoids the sine
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
function and the other trigonometric functions of angles. The angle at which two lines meet is determined by a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of their slopes, known as the spread between the two lines. The spread is equal to the square of the sine. The rational function can be identified without mentioning the sine function; see rational trigonometry
Rational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their...
for more on this.
Explicit formulas
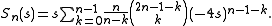 (S. Goh)
(S. Goh) (M. Hovdan)
(M. Hovdan)From the definition it immediately follows that
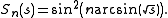
Relation to Chebyshev polynomials
The spread polynomials are related to the Chebyshev polynomialsChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the first kind, Tn by the identity
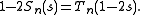
This implies
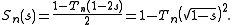
The second equality above follows from the identity
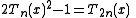
on Chebyshev polynomials.
Composition
The spread polynomials satisfy the composition identity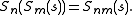
Coefficients in finite fields
When the coefficients are taken to be members of the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fp, then the sequence { Sn }n = 0, 1, 2, ... of spread polynomials is periodic with period (p2 − 1)/2. In other words, if k = (p2 − 1)/2, then Sn + k = Sn, for all n.
Orthogonality
When the coefficients are taken to be realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, then for n ≠ m, we have
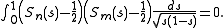
For n = m, the integral is π/8 unless n = m = 0, in which case it is π/4.
Generating functions
The ordinary generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
is
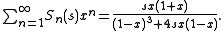
The exponential generating function is
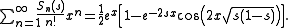
Differential equation
Sn(s) satisfies the second order linear homogenous differential equation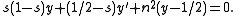
Use in rational trigonometry
Rational trigonometryRational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their...
is a recently introduced approach to trigonometry that eschews all transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s (such as sine, cosine, etc.), all measurements of angles or compositions of rotations, and characterizes the separation between lines by a quantity called the "spread", which is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of the slopes. Equality of angles between rays entails equality of spreads between lines. The spread between two lines is the square of the sine of the angle. The name "spread polynomials" comes from the use of these polynomials in rational trigonometry.
Table of spread polynomials, with factorizations
The first several spread polynomials are as follows:

