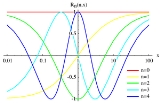
Chebyshev rational functions
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal
Orthogonal functions
In mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...
. They are named after Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
. A rational Chebyshev function of degree n is defined as:
where
is a Chebyshev polynomial of the first kind.Properties
Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves.Recursion
Differential equations
Orthogonality
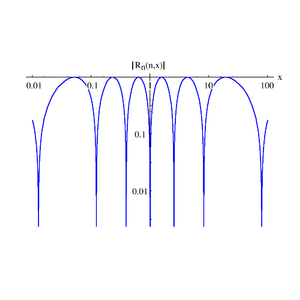
The orthogonality of the Chebyshev rational functions may be written:
where
equals 2 for n=0 and 
equals 1 for 
and 
is the Kronecker delta function.Expansion of an arbitrary function
For an arbitrary function
the orthogonality relationship can be used to expand 
:
where
Particular values
Partial fraction expansion
