Lissajous curve
Encyclopedia
In mathematics
, a Lissajous curve (icon and ˈ), also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equation
s
which describe complex harmonic motion
. This family of curve
s was investigated by Nathaniel Bowditch
in 1815, and later in more detail by Jules Antoine Lissajous
(a French name pronounced lisaˈʒu) in 1857.
The appearance of the figure is highly sensitive to the ratio a/b. For a ratio of 1, the figure is an ellipse
, with special cases including circles (A = B, δ = π
/2 radian
s) and lines
(δ = 0). Another simple Lissajous figure is the parabola
(a/b = 2, δ = π/2). Other ratios produce more complicated curves, which are closed only if a/b is rational
. The visual form of these curves is often suggestive of a three-dimensional knot, and indeed many kinds of knots, including those known as Lissajous knot
s, project to the plane as Lissajous figures.
.jpg)
Lissajous figures where a = 1, b = N (N is a natural number
) and
are Chebyshev polynomials
of the first kind of degree N.
fraction from 0 to 1 in steps of 0.01. (δ=0)
Below are examples of Lissajous figures with δ = π/2, an odd natural number
a, an even natural number
b, and |a − b| = 1.
.
(as illustrated). An octopus circuit
can be used to demonstrate the waveform
images on an oscilloscope. Two phase-shifted sinusoid inputs are applied to the oscilloscope in X-Y mode and the phase relationship between the signals is presented as a Lissajous figure.
On an oscilloscope, we suppose x is CH1 and y is CH2, A is amplitude of CH1 and B is amplitude of CH2, a is frequency of CH1 and b is frequency of CH2, so a/b is a ratio of frequency of two channels, finally, δ is the phase shift of CH1.
A purely mechanical application of a Lissajous curve with a=1, b=2 is in the driving mechanism of the Mars Light
type of oscillating beam lamps popular with railroads in the mid-1900s. The beam in some versions traces out a lopsided figure-8 pattern with the "8" lying on its side.
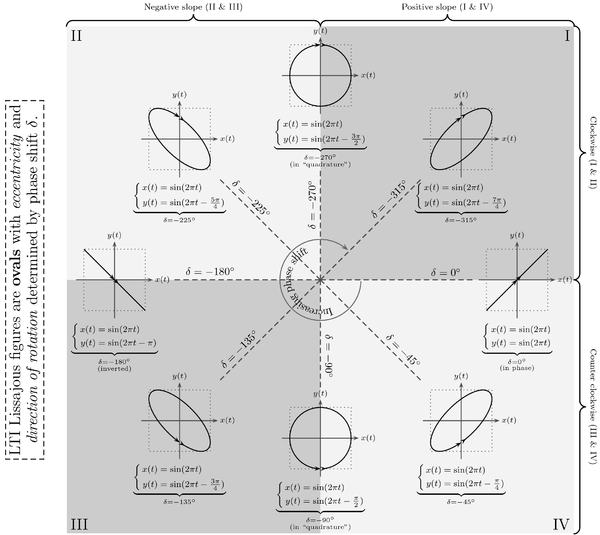
that can plot one signal against another (as opposed to one signal against time) to plot the output of an LTI system against the input to the LTI system produces an ellipse that is a Lissajous figure for the special case of a = b. The aspect ratio
of the resulting ellipse is a function of the phase shift between the input and output, with an aspect ratio of 1 (perfect circle) corresponding to a phase shift of
and an aspect ratio of 
(a line) corresponding to a phase shift of 0 or 180 degrees. The figure below summarizes how the Lissajous figure changes over different phase shifts. The phase shifts are all negative so that delay
semantics
can be used with a causal
LTI system (note that -270 degrees is equivalent to +90 degrees). The arrows show the direction of rotation of the Lissajous figure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lissajous curve (icon and ˈ), also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s
which describe complex harmonic motion
Complex harmonic motion
Complex harmonic motion occurs when a number of simple harmonic motions are combined.Chords in music are an example of this phenomenon.Any continuous periodic function can be represented as a complex harmonic motion using its fourier series....
. This family of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s was investigated by Nathaniel Bowditch
Nathaniel Bowditch
Nathaniel Bowditch was an early American mathematician remembered for his work on ocean navigation. He is often credited as the founder of modern maritime navigation; his book The New American Practical Navigator, first published in 1802, is still carried on board every commissioned U.S...
in 1815, and later in more detail by Jules Antoine Lissajous
Jules Antoine Lissajous
Jules Antoine Lissajous was a French mathematician, after whom Lissajous figures are named. Among other innovations, Lissajous invented the Lissajous apparatus, a device that creates the figures that bear his name...
(a French name pronounced lisaˈʒu) in 1857.
The appearance of the figure is highly sensitive to the ratio a/b. For a ratio of 1, the figure is an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, with special cases including circles (A = B, δ = π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
/2 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s) and lines
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
(δ = 0). Another simple Lissajous figure is the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
(a/b = 2, δ = π/2). Other ratios produce more complicated curves, which are closed only if a/b is rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. The visual form of these curves is often suggestive of a three-dimensional knot, and indeed many kinds of knots, including those known as Lissajous knot
Lissajous knot
In knot theory, a Lissajous knot is a knot defined by parametric equations of the formx = \cos,\qquad y = \cos, \qquad z = \cos,...
s, project to the plane as Lissajous figures.
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
) and
are Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the first kind of degree N.
Examples
The 20s animation below shows the curve adaptation with continuously increasing fraction from 0 to 1 in steps of 0.01. (δ=0)Below are examples of Lissajous figures with δ = π/2, an odd natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
a, an even natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
b, and |a − b| = 1.
Generation
Prior to modern computers, Lissajous curves could be generated mechanically by means of a harmonographHarmonograph
A harmonograph is a mechanical apparatus that employs pendulums to create a geometric image. The drawings created typically are Lissajous curves, or related drawings of greater complexity...
.
Practical application
Lissajous curves can also be generated using an oscilloscopeOscilloscope
An oscilloscope is a type of electronic test instrument that allows observation of constantly varying signal voltages, usually as a two-dimensional graph of one or more electrical potential differences using the vertical or 'Y' axis, plotted as a function of time,...
(as illustrated). An octopus circuit
Analog signature analysis
Analog signature analysis is electronic component and circuit board troubleshooting technique which applies a current-limited AC sinewave across two points of an electronic component or circuit....
can be used to demonstrate the waveform
Waveform
Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.In many cases the medium in which the wave is being propagated does not permit a direct visual image of the form. In these cases, the term 'waveform' refers to the shape of a graph...
images on an oscilloscope. Two phase-shifted sinusoid inputs are applied to the oscilloscope in X-Y mode and the phase relationship between the signals is presented as a Lissajous figure.
On an oscilloscope, we suppose x is CH1 and y is CH2, A is amplitude of CH1 and B is amplitude of CH2, a is frequency of CH1 and b is frequency of CH2, so a/b is a ratio of frequency of two channels, finally, δ is the phase shift of CH1.
A purely mechanical application of a Lissajous curve with a=1, b=2 is in the driving mechanism of the Mars Light
Mars Light
Mars Lights are signal-safety lights used in the United States and built by Mars Signal Light Company for railroad locomotives and fire apparatus...
type of oscillating beam lamps popular with railroads in the mid-1900s. The beam in some versions traces out a lopsided figure-8 pattern with the "8" lying on its side.
Application for the case of a = b
When the input to an LTI system is sinusoidal, the output is sinusoidal with the same frequency, but it may have a different amplitude and some phase shift. Using an oscilloscopeOscilloscope
An oscilloscope is a type of electronic test instrument that allows observation of constantly varying signal voltages, usually as a two-dimensional graph of one or more electrical potential differences using the vertical or 'Y' axis, plotted as a function of time,...
that can plot one signal against another (as opposed to one signal against time) to plot the output of an LTI system against the input to the LTI system produces an ellipse that is a Lissajous figure for the special case of a = b. The aspect ratio
Aspect ratio
The aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
of the resulting ellipse is a function of the phase shift between the input and output, with an aspect ratio of 1 (perfect circle) corresponding to a phase shift of
and an aspect ratio of (a line) corresponding to a phase shift of 0 or 180 degrees. The figure below summarizes how the Lissajous figure changes over different phase shifts. The phase shifts are all negative so that delayPropagation delay
Propagation delay is a technical term that can have a different meaning depending on the context. It can relate to networking, electronics or physics...
semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
can be used with a causal
Causal system
A causal system is a system where the output depends on past/current inputs but not future inputs i.e...
LTI system (note that -270 degrees is equivalent to +90 degrees). The arrows show the direction of rotation of the Lissajous figure.
Popular culture
- Lissajous figures are sometimes used in graphic designGraphic designGraphic design is a creative process – most often involving a client and a designer and usually completed in conjunction with producers of form – undertaken in order to convey a specific message to a targeted audience...
as logos. Examples include:- The Australian Broadcasting CorporationAustralian Broadcasting CorporationThe Australian Broadcasting Corporation, commonly referred to as "the ABC" , is Australia's national public broadcaster...
(a = 1, b = 3, δ = π/2) - The Lincoln LaboratoryLincoln LaboratoryMIT Lincoln Laboratory, located in Lexington, Massachusetts, is a United States Department of Defense research and development center chartered to apply advanced technology to problems of national security. Research and development activities focus on long-term technology development as well as...
at MIT (a = 4, b = 3, δ = 0) - The University of Electro-CommunicationsUniversity of Electro-CommunicationsThe is a national university in the city of Chōfu, Tokyo, Japan. It specialises in the disciplines of computer science, the physical sciences, engineering and technology. It was founded in 1918 .-Graduate schools:*Graduate School of Electro-Communications...
, Japan (a = 3, b = 4, δ = π/2).
- The Australian Broadcasting Corporation
- In computing, Lissajous figures are in some screen savers.
External links
- Interactive Java Tutorial: Lissajous Figures on Oscilloscope National High Magnetic Field Laboratory
- Lissajous Curve at Mathworld
- ECE 209: Lissajous Figures – a short wikified document that mathematically and graphically explains Lissajous curves for LTI systemsLTI system theoryLinear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
and gives an oscilloscopeOscilloscopeAn oscilloscope is a type of electronic test instrument that allows observation of constantly varying signal voltages, usually as a two-dimensional graph of one or more electrical potential differences using the vertical or 'Y' axis, plotted as a function of time,...
procedure that uses them to find system phase shiftPhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:... - HTML5 Canvas and Javascript based interactive version
- Animated Lissajous figures in Java
- About the Australian Broadcasting Corporation logo
- Free tool QLiss3D that displays Lissajous figures in three dimensions
- A free Javascript tool for generating Lissajous curves
- A 3D Java applet showing how a Lissajous figure can be traced.
- Lissajous 3D: animated textured 3D Lissajous patterns, also Lissajous screen saver for Windows
- http://jsxgraph.uni-bayreuth.de/wiki/index.php/Lissajous_curves: an interactive JavaScript-applet showing Lissajous curves in 2D. Neither Java nor Flash required, it uses the JSXGraph library.
- Another interactive Java applet; animated or can move figure with mouse.
- Lissajous Curves: Interactive simulation of graphical representations of musical intervals, beats, interference, vibrating strings
- Lissajous Curves: Interactive advanced Excel chart with infinite variation.