Splitting principle
Encyclopedia
In mathematics
, the splitting principle is a technique used to reduce questions about vector bundle
s to the case of line bundle
s.
In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct sums of line bundles. In this case the splitting principle can be quite useful.
Theorem: Splitting Principle: Let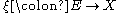
be a vector bundle of rank 
over a manifold 
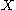. There exists a space 
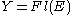, called the flag bundle associated to 
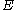, and a map 
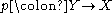such that
The line bundles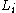
or their first characteristic class are called Chern roots.
The fact that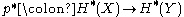
is injective means that any equation which holds in 
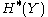(say between various Chern classes) also holds in 
.
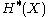The point is that these equations are easier to understand for direct sums of line bundles than for arbitrary vector bundles, so equations should be understood in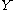
and then pushed down to 
.
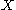, alternating polynomials) in the class of line bundles.
The Chern class
es and Pontryagin class
es correspond to symmetric polynomials: they are symmetric polynomials in the corresponding classes of line bundles (
is the kth symmetric polynomial in the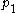 
of the line bundles, and so forth).
The Euler class
is an invariant of an oriented vector bundle, and thus the line bundles are ordered up to sign; the corresponding polynomial is the Vandermonde polynomial, the basic alternating polynomial
. Further, for an even dimensional manifold, its square is the top Pontryagin class, which corresponds to the square of the Vandermonde polynomial being the discriminant
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the splitting principle is a technique used to reduce questions about vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s to the case of line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s.
In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct sums of line bundles. In this case the splitting principle can be quite useful.
Theorem: Splitting Principle: Let
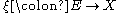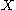be a vector bundle of rank over a manifold . There exists a space 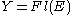, called the flag bundle associated to 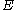, and a map 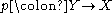such that- the induced cohomology homomorphism
is injective, and - the pullback bundle
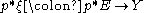breaks up as a direct sum of line bundles: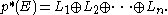 
The line bundles
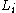or their first characteristic class are called Chern roots.The fact that
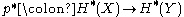is injective means that any equation which holds in 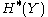(say between various Chern classes) also holds in 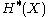.The point is that these equations are easier to understand for direct sums of line bundles than for arbitrary vector bundles, so equations should be understood in
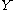and then pushed down to 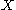.Symmetric polynomial
Under the splitting principle, characteristic classes correspond to symmetric polynomials (and for the Euler classEuler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
, alternating polynomials) in the class of line bundles.
The Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es and Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es correspond to symmetric polynomials: they are symmetric polynomials in the corresponding classes of line bundles (
is the kth symmetric polynomial in the 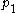of the line bundles, and so forth).The Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is an invariant of an oriented vector bundle, and thus the line bundles are ordered up to sign; the corresponding polynomial is the Vandermonde polynomial, the basic alternating polynomial
Alternating polynomial
In algebra, an alternating polynomial is a polynomial f such that if one switches any two of the variables, the polynomial changes sign:f = -f....
. Further, for an even dimensional manifold, its square is the top Pontryagin class, which corresponds to the square of the Vandermonde polynomial being the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
.
See also
- K-theoryK-theoryIn mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
- Grothendieck splitting principle for holomorphic vector bundles on the complex projective line